高斯消元法

· · 算法·理论

引入

矩阵是指若干数字排列成长方阵的形式，可以理解成二维数组。

我们可以利用矩阵表达 n 元一次线性方程组。例如，我们想解这个方程：

\left \{ \begin{matrix} \sum_{i=1}^na_{1i}x_i = b_1 \\ \sum_{i=1}^na_{2i}x_i = b_2 \\ \dots \\ \sum_{i=1}^na_{ni}x_i = b_n \end{matrix}\right.

则可以将其中的系数 a_{ij} 以及 b_i 放到一个 n \times (n+1) 的矩阵中：

\begin{bmatrix} a_{11}&a_{12}&\dots&a_{1n}&b_1 \\ a_{21}&a_{22}&\dots&a_{2n}&b_2 \\ \dots \\ a_{n1}&a_{n2}&\dots&a_{nn}&b_n \end{bmatrix}

我们称其为增广矩阵。

矩阵有三种初等变化，分别是：

事实上，我们平时手动解方程组时也是用这三步，所以我们可以完全将方程中的操作转移到矩阵上的操作。手动解方程的关键是尽量多的消元，即让尽量多的未知数的系数为 0。而接下来要介绍的高斯消元法与其思想相同。

相关定义

默认矩阵是 n \times n 的。

矩阵的对角线：所有 a_{i,i}。

单位矩阵：对角线上全是 1，其余为 0 的矩阵。通常称为 I，且满足 IA=AI=A。

矩阵的逆：若 AB=I，则 A,B 互逆，A 是 B 的逆，B 是 A 的逆；

上三角矩阵：对角线下方全为 0 的矩阵。即 i>j \Longrightarrow a_{i,j} =0。

单位上三角矩阵：对角线全为 1 的上三角矩阵。

高斯消元过程

高斯消元法，是指一个 n \times n 的矩阵通过上面的三种矩阵初等变化后，将矩阵消成单位上三角矩阵的过程。单位上三角矩阵形如：

\begin{bmatrix} 1&a_{12}’&a_{13}’&\dots&a_{1n}‘\\ 0&1&a_{23}’&\dots&a_{2n}’ \\ 0&0&1&\dots&a_{2n}’ \\ \dots \\ 0&0&0&\dots&1 \end{bmatrix}

如果我们对增广矩阵的左边（即忽略最后一列）进行高斯消元，且每一步对整行的操作时也改变最后一列的值，会得到：

\begin{bmatrix} 1&a_{12}’&a_{13}’&\dots&a_{1n}’&b_1'\\ 0&1&a_{23}’&\dots&a_{2n}’ &b_2'\\ 0&0&1&\dots&a_{2n}’ &b_3'\\ \dots \\ 0&0&0&\dots&1&b_n' \end{bmatrix}

这样有什么好处呢？我们通过最后一行能得到 x_n = b'_n，再通过倒数第二行能得到 x_{n-1}=b_{n-1}'-a_{n-1,n}'x_n，以此类推就可以解出 x_1 \dots x_n。反推这一步是 \mathcal O(n^2) 的。

现在考虑如何通过三种矩阵初等变换将一个矩阵消成单位上三角矩阵，即高斯消元法的过程。

\begin{bmatrix} a_{11}&a_{12}&\dots&a_{1n} \\ a_{21}&a_{22}&\dots&a_{2n} \\ \dots \\ a_{n1}&a_{n2}&\dots&a_{nn} \end{bmatrix}

首先找到某个 a_{i1} \ne 0 的 i，将第 i 行交换到第一行。

将第一行全部除以 a_{11}。即第一行变为：

\begin{bmatrix} 1&a_{12}/a_{11}&\dots&a_{1n}/a_{11} \end{bmatrix}

然后依次考虑下面的行。对于第 i 行，我们将第一行的 -a_{i1} 倍加到第 i 行上。那么这一行的第一个数就变为 0 了。

也就是说，上面的操作可以使得第一列上的第一个数变为 1，剩下的变为 0。

此时第一行和第一列都变成我们想要的样子了。先暂时删掉方便后续操作。

\begin{bmatrix} a_{22}'&\dots&a_{2n}' \\ \dots \\ a_{n2}'&\dots&a_{nn}' \end{bmatrix}

同样的，找到某个 i 使得 a_{i2} \ne 0，将第 i 行交换到第一行。然后将第一行同时除以 a_{11}，并将下面的每一行加上第一行的 -a_{i1} 倍。

这样就变成了一个不断迭代的问题。我们可以在 \mathcal O(n^3) 的复杂度内解决。

还有一个问题。如果我们找不到某个 a_{i1} \ne 0 的 i，即当前的第一列全为 0，那么这个方程组是无解或有无穷组解的。实际应用中一般不需要考虑解的判定（虽然模板题需要）。

举个例子

\begin{bmatrix} 2 &-1 &1& 1 \\ 4 &1 &-1 &5 \\ 1 &1& 1 &0 \\ \end{bmatrix}

发现 2 \ne 0，那么不用交换了。

将第一行除以 2：

\begin{bmatrix} 1 &-1/2 &1/2& 1/2 \\ 4 &1 &-1 &5 \\ 1 &1& 1 &0 \\ \end{bmatrix}

将第二行和第三行分别加上第一行的 -4 倍和 -1 倍：

\begin{bmatrix} 1 &-1/2 &1/2& 1/2 \\ 0 &3 &-3 &3 \\ 0 &3/2& 1/2 &-1/2 \\ \end{bmatrix}

将第二行除以 3：

\begin{bmatrix} 1 &-1/2 &1/2& 1/2 \\ 0 &1 &-1 &1 \\ 0 &3/2& 1/2 &-1/2 \\ \end{bmatrix}

将第三行加上第二行的 -3/2 倍：

\begin{bmatrix} 1 &-1/2 &1/2& 1/2 \\ 0 &1 &-1 &1 \\ 0 &0& 2 &-2 \\ \end{bmatrix}

将第三行除以 2：

\begin{bmatrix} 1 &-1/2 &1/2& 1/2 \\ 0 &1 &-1 &1 \\ 0 &0& 1 &-1 \\ \end{bmatrix}

由第三行得 x_3 = -1。由第二行得 x_2 = 1 + x_3 = 0。由第一行得 x_1 = 1/2 - 1/2x_3 + 1/2x_2 = 1。

高斯约旦消元

与高斯消元唯一不同的是，我们将第 i 行的开头消成 1 后，不是用 i 行消 i +1\sim n 行，而是所有行（除自己）。这样操作后的矩阵是一个单位矩阵，即对角线上的值全为 1，除对角线外的值全为 0。求方程解时直接 x_i = a_{i,n+1} 即可。

例题

P2455 [SDOI2006] 线性方程组，P3389 【模板】高斯消元法：模板题。

P4783 【模板】矩阵求逆：在原矩阵右边放一个单位矩阵，对左边做高斯约旦消元。此时左边是单位矩阵，右边即为原方程的逆。

P2447 [SDOI2010] 外星千足虫：异或方程组。

P3164 [CQOI2014] 和谐矩阵：同上。

与概率 DP 的结合

事实上，DP 的转移本质是一个方程式。只不过一般的 DP 并不需要真正解方程，因为它们有特定的求解顺序，例如背包计数 f(i,j) = f(i-1,j) + f(i-1,j-w_i)，其中 f(i-1,j) 和 f(i-1,j-w_i) 已经求好了。那么这是一个代数式求值问题。

而与随机游走有关的问题通常会用到概率 DP。这类问题的显著特征是，从一个点出发后可能经过若干步回到自身，即 DP 时并没有特定的转移顺序，或者说会出现转移成环。

例如图上随机游走问题中用到了一个转移式 f(u) = \dfrac{\sum_{(u,v) \in E} f(v)}{deg_u}+1，此时不应以代数式求值的视角看待 DP，而应将一个转移式看成一个 n 元线性方程。

那么 n 个状态会对应 n 个线性方程。我们可以使用高斯消元法解决这类问题。

非常规高斯消元求解概率 DP 例题

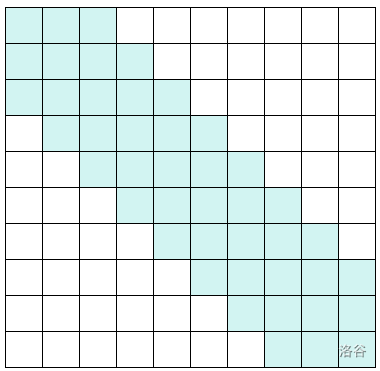
但是一般的概率问题抽象成方程组后得到的矩阵会带有一些特点，如下文介绍的 Band-Matrix。或许我们可以进行复杂度上的优化。 Band-Matrix，即带状矩阵，顾名思义，是一种类似于长条状的矩阵。它看上去像是给对角线“加宽”了。 ![](https://cdn.luogu.com.cn/upload/image_hosting/t0nkwybw.png) 除蓝色部分外的值均为 $0$。 令这个”长条“的”宽度“为 $d$。如上图 $d=2$。那么我们可以在 $\mathcal O(nd^2)$ 的时间复杂度内将其消成上三角矩阵。 形式化的，对于所有 $a_{i,j} = 0$，都满足 $|i-j| > d$。则 $d$ 是满足条件的最小值。 消元过程是类似，我们只需要人为规避掉 $0$ 的位置。具体的： - 将第一行的前 $d$ 个数除以 $a_{11}$； - 将第 $2\sim d$ 行加上第一行的 $-a_{i,1}$ 倍。这里实际发生改变的位置只有 $\mathcal O(d^2)$ 个，其余都是 $0 \to 0$，不必浪费复杂度。 - 然后操作下一行，以此类推。 **注意带状矩阵是不能高斯约旦消元的**。感性理解上面的行中不止是带状对角线上非 $0$，其余位置也可能在消元过程中变成非 $0$，如果再去改它复杂度不对，否则正确性不对。因此只能使用普通的高斯消元。 ```cpp void gauss(int n, int d) { for (int s = 1; s <= n; ++ s ) { double k = a[s][s]; for (int i = s; i <= min(n, s + 2 * d); ++ i ) a[s][i] /= k; a[s][n + 1] /= k; for (int i = s + 1; i <= min(n, i + 2 * d); ++ i ) { double k = a[i][s]; for (int j = max(1, i - 2 * d); j <= min(n, i + 2 * d); ++ j ) { a[i][j] -= k * a[s][j]; } a[i][n + 1] -= k * a[s][n + 1]; } } } ``` 这一类问题应用范围是很广的。 ### CF24D Broken robot 不难得到 DP 方程： $$ f(n,i)=0 \\ f(i,1)=\dfrac{f(i,1)+f(i+1,1)+f(i,2)}3 + 1 \\ f(i,m)=\dfrac{f(i,m)+f(i+1,m)+f(i,m-1)}3 + 1 \\ f(i,j)=\dfrac{f(i,j)+f(i+1,j)+f(i,j+1)+f(i,j-1)}4 + 1 $$ 即： $$ 2f(i,1)-f(i+1,1)-f(i,2)=3\\ 2f(i,m)-f(i+1,m)-f(i,m-1)=3 \\ 3f(i,j)-f(i+1,j)-f(i,j+1)-f(i,j-1)=4 $$ 此时有 $nm$ 个未知数。直接高斯消元是 $\mathcal O(n^3m^3)$ 的。 注意到第 $i$ 行一定从第 $i+1$ 行转移过来，因此我们可以从第 $n$ 行倒着求解，即： $$ 2f(i,1)-f(i,2)=3+f(i+1,1)\\ 2f(i,m)-f(i,m-1)=3+f(i+1,m) \\ 3f(i,j)-f(i,j+1)-f(i,j-1)=4+f(i+1,j) $$ 此时复杂度是 $\mathcal O(nm^3)$。 我们把矩阵画出来看一下（$m=5$）： $$ \begin{bmatrix} 2&-1&0&0&0\\ -1&3&-1&0&0 \\ 0&-1&3&-1&0 \\ 0&0&-1&3&-1 \\ 0&0&0&-1&2 \end{bmatrix} $$ 发现这是一个 $d=1$ 的带状矩阵。于是高斯消元复杂度降到 $\mathcal O(nm)$。 ### CF963E Circles of Waiting ~~woc 是黑题！！！还是 CF3100*！！！！~~ 较为类似。设 $f(x,y)$ 表示从 $x,y$ 出发，移动至距离原点距离为大于 $R$ 的点的期望步数。 容易得出转移方程，$f(x,y)$ 从 $f(x \pm 1, y \pm 1)$ 转移而来。 $$ f(x,y) = f(x+1,y)a_1 + f(x,y+1)a_2 + f(x-1,y)a_3 + f(x,y-1)a_4 + 1 $$ 显然转移成环，因此转化成高斯消元解方程组的问题。 估计一下状态数是 $\pi R^2$ 级别的，差不多 $8000$。直接做 $8000^3$ 显然不行。 我们为每个不为 $0$ 的状态进行编号。$f(x,y)$ 不为 $0$ 等价于 $x^2+y^2 \le r^2$。我们将这些状态按照从上往下从左往右的顺序编号，那么若 $f(x,y)$ 编号为 $i$，那么与其相关的 $f(x\pm 1,y \pm 1)$ 的编号与其最多相差 $2r+1$。 也就是说建成的矩阵是一个带宽为 $2r+1$ 的带状矩阵，可在 $\mathcal O(r^4)$ 内解决。 ### P4457 [BJOI2018] 治疗之雨 ~~woc 这也是黑题！！~~ 设 $f(i)$ 表示这一回合掉 $i$ 滴血的概率。 $$ f(i) = \left(\dfrac 1{m+1}\right)^i\left(\dfrac m{m+1}\right)^{k-i} \dbinom ki $$ 因为 $k$ 很大，所以直接求 $\dbinom ki$ 是困难的。注意到： $$ \dfrac{f(i+1)}{f(i)} = \dfrac{\left(\dfrac 1{m+1}\right)^{i+1}\left(\dfrac m{m+1}\right)^{k-i-1} \dbinom k{i+1}}{\left(\dfrac 1{m+1}\right)^i\left(\dfrac m{m+1}\right)^{k-i} \dbinom ki} = \dfrac{k-i-1}{mi} $$ 设剩余 $i$ 滴血时，期望 $g(i)$ 回合后会死。 $$ g(i) = \left\{ \begin{matrix} \dfrac m{m+1} \sum_{j=0}^i f(i-j)g(j)+\dfrac 1{m+1}\sum_{j=0}^{i+1} f(i+1-j)g(j)+1 &,i < n \\ \sum_{j=0}^i f(i-j)g(j) + 1 &,i=n \end{matrix}\right. $$ 直接高斯消元仍然是 $\mathcal O(n^3)$ 的，不可接受。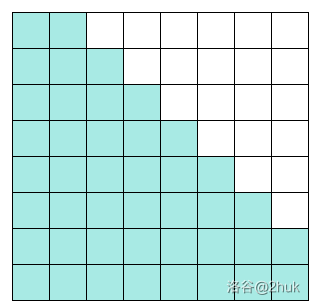 我们将将矩阵画出来，白色位置是 $0$： ![](https://cdn.luogu.com.cn/upload/image_hosting/tw86wclt.png) 这很像一个下三角矩阵，只不过对角线上方多了一格。 与 band-matrix 的消元思想类似。我们用最后一行消第倒数第二行，将 $a_{n-1,n}$ 变成 $0$；再用倒数第二行消倒数第三行，将 $a_{n-2,n-1}$ 消成 $0$，以此类推。这样总共消 $n$ 次，每次 $\mathcal O(n)$，总复杂度就降到了 $\mathcal O(n^2)$。