题解 P6275 【[USACO20OPEN]Sprinklers 2: Return of the Alfalfa P】

ez_lcw · 2020-05-16 11:31:39 · 题解

先讲一下等会要用到的定义：

红格代表被甜玉米洒水器喷洒到的方格，蓝格代表被苜蓿洒水器喷洒到的方格。橙格代表有甜玉米洒水器的方格，紫格代表有苜蓿洒水器。
比如下面这个图中，黄**点**代表的是 $(4,3)$，黄**格**代表的是 $[2,3]$。 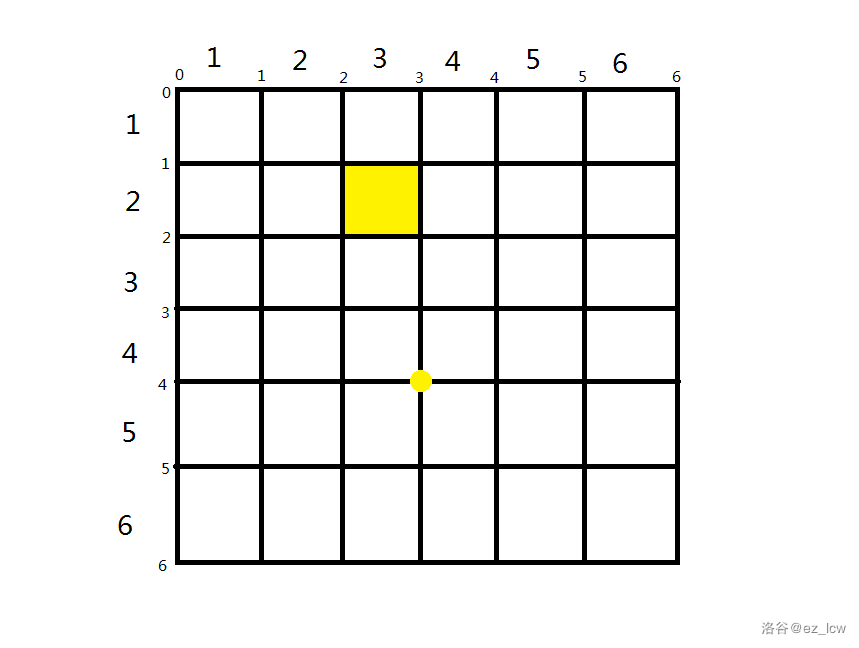![](https://cdn.luogu.com.cn/upload/image_hosting/edr2jjqh.png)

~~然后说说考试时的心路历程。~~（其实是用来帮助你如何由暴力思考到正解的）

25\ pts

第一眼看到这道题是不会的……~~甚至连部分分都不知道怎么写~~

但是仔细想了一想，发现红蓝两方阵营肯定是被一条由 (0,0) 到 (n,n) 的分割线分开的。

比如说这样：

这种情况是被如图的黄色的分割线分开的。

然后考虑哪些地方需要洒水器：

显然，我们发现，在分割线的拐角处都需要洒水器（即图中的橙格和紫格），其他地方可填可不填，但是只能填一种洒水器。

我们假设某一种分割线有 k 个拐角（也就是有 k 个洒水器是一定要放的），方阵总面积为 S（面积指没有被占据的网格的总数）。

那么对于这种分割线，一共有 2^{S-k} 种方案。（记住这条公式）

那么暴力的方法就显而易见了：每次枚举一条分割线，并记录分割线的拐角数，最后统计答案。

时间复杂度貌似是 O(2^n+n^2)，只有 25pts。

代码：

#include<bits/stdc++.h>

#define N 2010
#define mod 1000000007

using namespace std;

int n,ans,poww[N*N],sum;
char ch[N][N];

//n=4
// 0 1 2 3 4 
//0#########
// #.#.#W#.#
//1#########
// #.#.#W#W#
//2#########
// #W#W#.#.#
//3#########
// #.#.#.#W#
//4#########

//last=0向下，last=1向上 

void dfs(const int x,const int y,const int a,const int b,const int last)
{
    if(x==n&&y==n)
    {
        ans=(0ll+ans+1ll*poww[sum-a-b])%mod;
        return;
    }
    if(!last)
    {
        if(x+1<=n) dfs(x+1,y,a,b,0);
        if(y+1<=n&&ch[x][y+1]!='W') dfs(x,y+1,a,b+1,1);
    }
    else
    {
        if(x+1<=n&&ch[x+1][y]!='W') dfs(x+1,y,a+1,b,0);
        if(y+1<=n) dfs(x,y+1,a,b,1);
    } 
}

inline int read()
{
    int x=0;
    char ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9')
    {
        x=(x<<1)+(x<<3)+(ch^'0');
        ch=getchar();
    }
    return x;
}

int main()
{
    n=read();
    poww[0]=1;
    for(register int i=1;i<=n*n;i++) poww[i]=(2ll*poww[i-1])%mod;
    for(register int i=1;i<=n;i++) scanf("%s",ch[i]+1);
    for(register int i=1;i<=n;i++)
        for(register int j=1;j<=n;j++)
            sum+=(ch[i][j]=='.');
    dfs(1,0,0,0,0);
    dfs(0,1,0,0,1);
    printf("%d\n",ans);
    return 0;
}

100\ pts

考虑 dp，设 dp(i,j,0/1) 指已经把前 i 行灌溉满了，分割线的终止在 (i,j)，分割线最后的方向是向右/向下的。

那么答案显然就是 dp(n,n,0)+dp(n,n,1)。

考虑状态转移方程。

先考虑 dp(i,j,0) 怎么转移：

如图，我们现在要求出 dp(3,3,0)（黄点），那么只能从 dp(3,2,0/1)（绿点）转移，因为分割线最后的方向是向右的。

第一种情况：从 dp(3,2,0) 转移，如图：

那么显然有 dp(3,3,0)=dp(3,2,0)，因为 S 没变，k 也没变。

第二种情况：从 dp(3,2,1) 转移，如图：

我们发现，原来的分割线终止在 (3,2) 时，k=1，就是只有 [1,2] 一个灌溉器，但是现在分割线种植在 (3,3) 时，k=2，也就是新增了一个灌溉器 [3,3]。那么原来的方案数 dp(3,2,1)=2^{S-k}，现在 k\gets k+1，所以 dp(3,3,0)=\frac{dp(3,2,1)}{2}。

整合一下，就有 dp(3,3,0)=dp(3,2,0)+\frac{dp(3,2,1)}{2}。

即 dp(i,j,0)=dp(i,j-1,0)+\frac{dp(i,j-1,1)}{2}
考虑 dp(i,j,1) 怎么转移：

同理，这次需要从绿点转移：

第一种情况：从 dp(2,3,0) 转移，如图：

第一幅图是 dp(2,3,0) 的情况，第二幅图是 dp(3,3,1) 的情况。

显然从第一幅图变成第二幅图时 S 增加了 sum_3，k 增加了 1，那么 dp 值从 2^{S-k} 变成了 2^{S+sum_3-k-1}，也就是说 dp(3,3,1)=dp(2,3,0)\times 2^{sum_3-1}。

第二种情况：从 dp(2,3,1) 转移，如图：

然后我们发现，S\gets S+sum_3，k 没变，则 dp(3,3,1)=dp(2,3,1)\times 2^{sum_3}

整合一下，dp(3,3,1)=dp(2,3,0)\times 2^{sum_3-1}+dp(2,3,1)\times 2^{sum_3}。

即 dp(i,j,1)=dp(i-1,j,0)\times 2^{sum_i-1}+dp(i-1,j,1)\times 2^{sum_i}。

到这里，整道题就做完了，已经可以 AC 了。

时间复杂度 O(n^2)。

但是还有一些可以优化的地方，这里就大致讲一下，就是把求面积的部分直接提出来，放到最后输出的时候乘上一个 2^{\sum_{i=1}^n sum_i}（也就是全局的面积）就好了。

代码（未加优化）：

#include<bits/stdc++.h>

#define N 2010
#define mod 1000000007
#define half 500000004

using namespace std;

void add(int &a,int b){a=(0ll+a+b)%mod;}
int mul(int a,int b){return (1ll*a*b)%mod;}

int n,dp[N][N][2],sum[N],poww[N*N];
char ch[N][N];

int main()
{
    scanf("%d",&n);
    poww[0]=1;
    for(int i=1;i<=n*n;i++)
        poww[i]=mul(2,poww[i-1]);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",ch[i]+1);
        for(int j=1;j<=n;j++) 
            sum[i]+=(ch[i][j]=='.');
    } 
    dp[0][0][0]=dp[0][0][1]=1;
    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<=n;j++)
        {
            if(!i&&!j) continue;
            if(j>0)
            {
                add(dp[i][j][0],dp[i][j-1][0]);
                if(ch[i][j]=='.') add(dp[i][j][0],mul(dp[i][j-1][1],half));
            }
            if(i>0)
            {
                add(dp[i][j][1],mul(dp[i-1][j][1],poww[sum[i]]));
                if(ch[i][j]=='.') add(dp[i][j][1],mul(dp[i-1][j][0],poww[sum[i]-1]));
            }
        }
    }
    printf("%d\n",(0ll+dp[n][n][0]+dp[n][n][1])%mod);
    return 0;
}

代码（加优化）：

#include<bits/stdc++.h>

#define N 2010
#define mod 1000000007
#define half 500000004

using namespace std;

void add(int &a,int b){a=(0ll+a+b)%mod;}
int mul(int a,int b){return (1ll*a*b)%mod;}

int n,dp[N][N][2],sum;
char ch[N][N];

int poww(int a,int b)
{
    int ans=1;
    while(b)
    {
        if(b&1) ans=(1ll*ans*a)%mod;
        a=(1ll*a*a)%mod;
        b>>=1;
    }
    return ans;
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",ch[i]+1);
        for(int j=1;j<=n;j++) 
            sum+=(ch[i][j]=='.');
    } 
    dp[0][0][0]=dp[0][0][1]=1;
    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<=n;j++)
        {
            if(!i&&!j) continue;
            if(j>0)
            {
                add(dp[i][j][0],dp[i][j-1][0]);
                if(ch[i][j]=='.') add(dp[i][j][0],mul(dp[i][j-1][1],half));
            }
            if(i>0)
            {
                add(dp[i][j][1],dp[i-1][j][1]);
                if(ch[i][j]=='.') add(dp[i][j][1],mul(dp[i-1][j][0],half));
            }
        }
    }
    printf("%d\n",1ll*(dp[n][n][0]+dp[n][n][1])%mod*poww(2,sum)%mod);
    return 0;
}

~~其实就是常数上的优化。~~

~~写码不易，留赞再走。~~