题解:AT_arc165_f [ARC165F] Make Adjacent
Lyrella
·
·
题解
前言
# 简要题意
给你一个长度为 $2n$ 的序列满足 $\forall a_i\in[1,n]$,其中 $1$ 到 $n$ 每个数都出现了两次,现在需要把相同的两个数排到一起,每次操作只能交换相邻两个数,在**保证操作次数最小**的情况下求出现在序列的**最小字典序**。
数据范围:$1\le n\le2\times10^5$。
# 思路
做题的时候首先应该考虑题目性质,可以从手玩样例开始。因为最后并没有让你求最少操作次数,所以我们只用讨论**数与数之间的关系**。我们考虑最简单的情况:假设现在序列中只有 $1$ 和 $2$ 各两个,一共存在六种可能的情况。我们先将他们列出来:
1. $1122
-
1212
-
1221
-
2112
-
2121
-
2211
对于第一种和第六种情况我们可以不用考虑,因为需要保证操作数最小。然后这四种情况实际只有两种本质不同,我们将他们抓出来。假设有两数 A,B 位置关系如下:
对于第一个情况,我们只需将中间两数交换即可。而第二种,我们既可以将第一个数交换到第三个位置,也可以将最后一个数交换到第二个位置。也就是说:第一种情况下数的位置决定最后顺序;而第二种情况下数的大小决定了最后顺序。
现在考虑扩展这两种情况,对于数列中任意的两数 A,B,如果满足 A\dots B\dots A\dots B 的形式,我一定会让 A 排在 B 前面;如果满足 A\dots B\dots B\dots A 的形式,我就会去考虑两个数之间的大小关系。
总结一下:
可是直接建图跑是 $O(n^2)$ 的,考虑优化。我们把每一个关于 $i$ 的二元组 $(a_i,b_i)$ 看成平面内的点,若 $i,j$ 之间连边则需要满足上述偏序。我们可以考虑分治建图,也就是类似 $\text{cdq}$ 的过程,具体见下图:
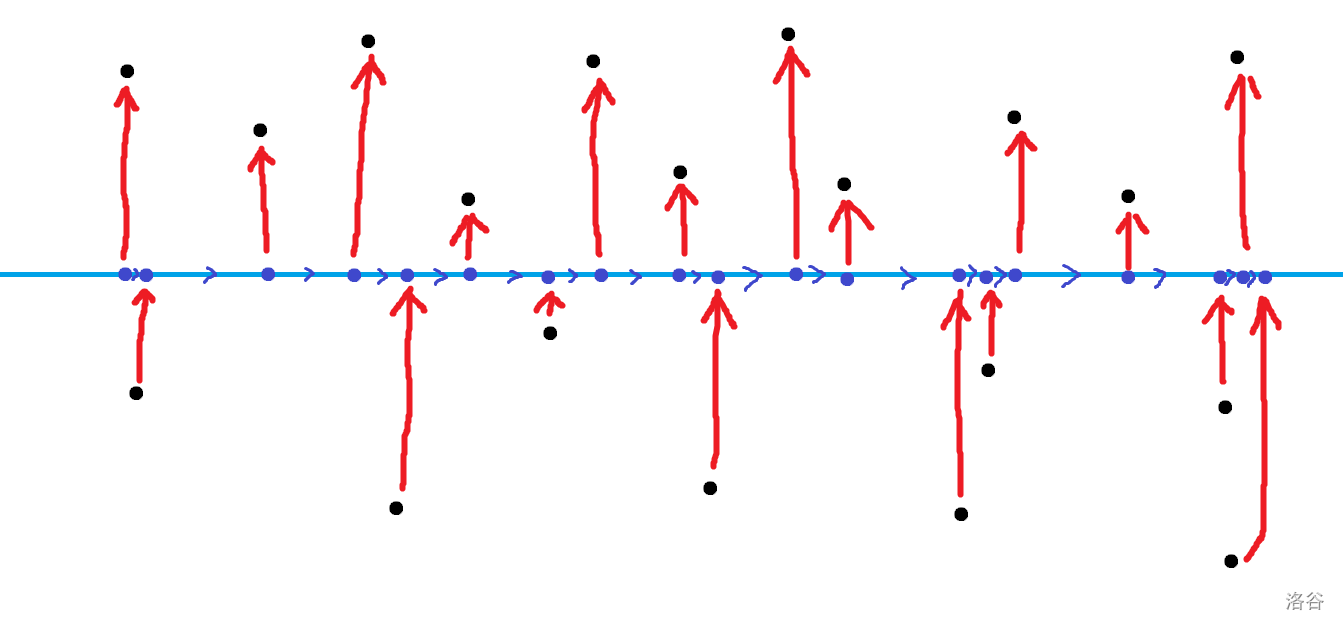
我们横着切一刀把平面分成两部分,在分割线上建一些虚点。对于下面的实点垂直向上连边,上面的实点从下面虚点往上连边,然后虚点之间从左往右连。若每次在中间切最多切出 $\log n$ 层,所以只有 $n\log n$ 个点和边。但是拓扑的时候如果用优先队列是两只 $\log$ 的,考虑继续优化。
其实我们只需要对实点用优先队列,对于虚点我们不关心他们的具体顺序,所以开一个普通队列存虚点,另一个优先队列存实点,每次先把所有普通队列的点拓扑完再去拓扑优先队列就行。时间复杂度是 $O(n\log n)$ 的,因为实点只有 $n$ 个。
# 代码
```cpp
void cdq(int l, int r){
if(l == r)return; int mid = l + r >> 1, lim = a[mid].l;
cdq(l, mid), cdq(mid + 1, r);
int i = l, j = mid + 1, k = l;
while(i <= mid and j <= r)a[i].r < a[j].r ? b[k++] = a[i++] : b[k++] = a[j++];
while(i <= mid)b[k++] = a[i++]; while(j <= r)b[k++] = a[j++];
for(int i = l; i <= r; ++i){
a[i] = b[i], ++nd; if(i ^ l)e[nd - 1].pb(nd), ++in[nd];
if(a[i].l <= lim)e[a[i].id].pb(nd), ++in[nd];
else e[nd].pb(a[i].id), ++in[a[i].id];
}
}
void upd(int x){
if(in[x])return;
x <= n ? q.push(x) : qc.push(x);
}
signed main(){
freopen("swap.in", "r", stdin);
freopen("swap.out", "w", stdout);
n = rd(), nd = n << 1;
for(int i = 1; i <= nd; ++i){
int x = rd();
if(a[x].l)a[x].r = i; else a[x].l = i, a[x].id = x;
}
sort(a + 1, a + 1 + n); nd = n;
cdq(1, n);
for(int i = 1; i <= nd; ++i)upd(i);
while(! q.empty() or ! qc.empty()){
while(! qc.empty()){
int u = qc.front(); qc.pop();
for(int v : e[u])--in[v], upd(v);
}
if(q.empty())return 0;
int u = q.top(); q.pop();
pc(u), putchar(' '), pc(u), putchar(' ');
for(int v : e[u])--in[v], upd(v);
}
return 0;
}
```