P7731 题解

kyBWE · 2021-07-27 11:33:29 · 题解

P7731题解

题意简述

起点为第 x_1 部电梯且横坐标为 y_1(横坐标是 y 就及其别扭)，终点为第 x_2 部电梯且横坐标为 y_2，换乘一次电梯花费 1 ZMB（注意所有电梯都是向右走的）。

题目分析

通过简单的分析可以得知，如果能到达终点，那么至多需要换乘两次电梯。

证明

• 情况一
  
  如果起点和终点在同一部电梯上（即在同一条直线上），并且起点在终点左侧，显然不需要换乘即可到达。
  此时需要满足 x_1=x_2 且 y_1≤y_2 （注意 y_1 可以等于 y_2，即起点和终点相同）。

• 情况二
  如果起点所在直线 x_1 和和终点所在直线 x_2 有交点且交点位于 y_1,y_2 之间，那么只需在交点处换乘一次即可到达。
  此时需要满足 y_1 ≤ 交点横坐标 ≤ y_2。（如果 y_1=y_2= 交点横坐标，那显然 y_1,y_2 在一条直线上，若为这种情况则已经在情况一中判断并输出结果了，所以不用担心误判）
  顺便来推一下交点坐标：设交点坐标为 (x_0,y_0)，那么我们可以得到方程组

  y_0=k[x_1]*x_0+b[x_1] y_0=k[x_2]*x_0+b[x_2]

  上减下可以得到

  (k[x_1]-k[x_2])*x_0=b[x_2]-b[x_1]

  由此我们很容易就能得出交点横坐标 x_0 的关系式。

• 情况三

如果直线 x_1 和直线 x_2 的交点位于 y_1,y_2 两侧，有一条直线分别与 x_1,x_2 交于点 xj_1,xj_2，若两交点位于 y_1,y_2 之间且 xj_1≤xj_2，那么只需在 xj_1 和 xj_2 两点各换乘一次即可到达
此时需要满足 y_1≤xj_1≤xj_2≤y_2，所以我们可以枚举每一条直线的 k 和 b，并算出相应的 xj_1 和 xj_2，判断是否满足条件。

• 除上述三种情况外，其他情况都不能达到。
  我们顺便来看一下不能到达的情况：
  2. 
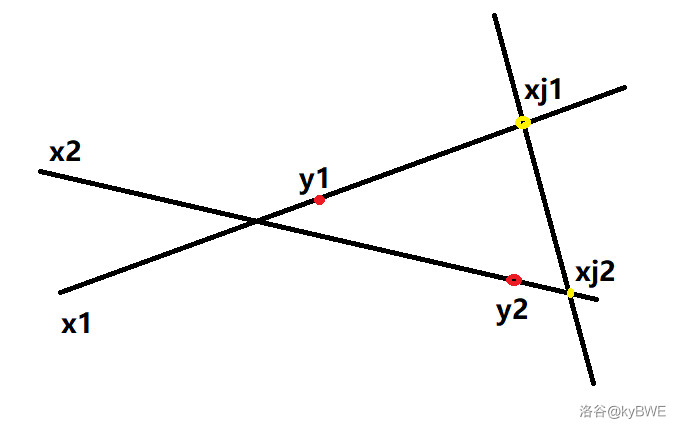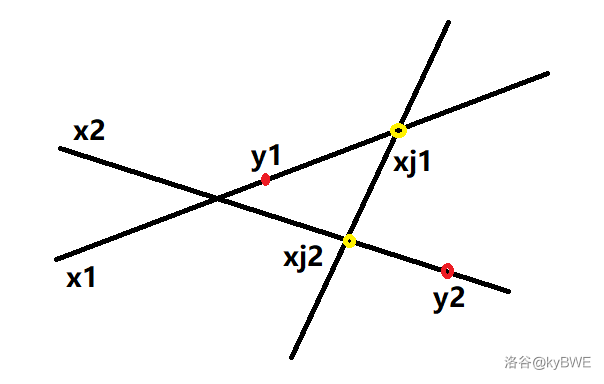  3.  （因为电梯只能向右走，所以无法从 $xj_1$ 到达 $xj_2$）

最后附上AC代码

    #include <iostream>
    using namespace std;
    int k[100005],b[100005];
    int main()
    {
        int n,x1,x2,y1,y2;
        cin>>n;
        cin>>x1>>y1>>x2>>y2;
        for(int i=1;i<=n;i++)
            cin>>k[i]>>b[i];
        if(x1==x2&&y1<=y2)//情况一 
        {//y1,y2在一条直线上 
            cout<<"0";
            return 0;//直接结束程序防止后面误判 
        }
        //情况二 
        double x0=(b[x2]-b[x1])*1.0/(k[x1]-k[x2]);
        //先求出交点横坐标（注意要 *1.0把 k和 b转成 double型） 
        if(y1<=x0&&y2>=x0)
        {
            cout<<"1";
            return 0;
        }
        //情况三 
        for(int i=1;i<=n;i++)//枚举每一条直线 
        {
            double xj1=(b[i]-b[x1])*1.0/(k[x1]-k[i]);
            double xj2=(b[x2]-b[i])*1.0/(k[i]-k[x2]);
            //先求出两交点 xj1，xj2的横坐标 
            if(y1<=xj1&&xj1<=xj2&&xj2<=y2)
            {
                cout<<"2";
                return 0;
            }
        }
        //若上述三种都不满足，则无法到达 
        cout<<"-1";//输出-1走人 
        return 0;
    }

蒟蒻的第一篇题解qvq