大砖数学(二)多项式基础
Amidst
·
·
算法·理论
前言
原本这篇和第一篇是放在一起的,后来想想还是分开了。
糖丸 CSDN 连第一篇都得分两部分传。
多项式基础章节为幼儿园中班难度,如果您已经上过幼儿园中班,建议跳过。
快速傅里叶变换
恭喜你看完了第一篇的两万字废话,下面要讲的跟第一篇一点关系都没有。
快速傅里叶变换(FFT)是一种可以在 O(n\log n) 时间内计算多项式乘法的算法。当然,大整数也可以视为一个多项式,所以 FFT 也用于加速大整数乘法的计算。
FFT 神秘历史
1807 年,傅里叶完成了一项研究,他发现在表示一个物体的温度分布时,成谐波关系的正弦函数级数是非常有用的。另外,他还断言:“任何”周期信号都可以用这样的级数来表示。然而他假了。虽然在这一问题上他的论述很有意义,但隐藏在这后面的很多基本概念已经被其他科学家发现;同时傅里叶的数学证明也不够完善。直到 1829 年,狄利克雷给出若干精确条件,把这个烂摊子收了,在这些条件下,一个周期信号才可以用一个傅里叶级数表示。因此,傅里叶其实并没有对傅里叶级数的数学理论做出什么贡献。
1963 年 8 月美、英、苏三国在莫斯科谈判,达成协议签定了该条约,全称为《关于禁止在大气层、外层空间和水下进行核武器爆炸实验的条约》,又称《部分核禁止条约》或三家条约。可以注意到,条约中不包括地下核武器爆炸实验,这是因为地下核实验难以被检测到,大地隔绝了大部分的辐射,声音。使得其难以想地上或水下核试验一样容易被探测到。要想探测地下核试验,主要靠分析地动信息。但如何将日常地震活动造成的地动与核试验造成的地动区分开来成为了当时科学家所难以解决的问题。在快速傅里叶算法还未发现之前,按照离散傅里叶定义使用计算机对地动信号做频谱分析,算力远远不足,分析出的数据严重过时。因此在这个背景下,FFT 出现了。
复数和复平面就不讲了,这个幼儿园小小班就学过。
自然对数底数在复平面上的意义
在复平面上,复数 e^{j\theta} 表示一个绕原点逆时针旋转的操作,旋转角度为 \theta。这表明复数 e^{j\theta} 是一个单位圆上的点,其模长为 1,辐角为 \theta。在复平面上,复数的模长和辐角分别对应于其在单位圆上的位置和旋转角度。
单位根
我们补充对上一篇中复系数多项式因式分解定理的说明,上一篇中提到,n 次系数多项式恰有 n 个复根。
我们补充,这 n 个复根在复平面上等分单位圆,我们记其为单位根,将第 i 个单位根记为 \omega_n^{i-1},这说明,1 一定是第一个单位根。
根据我们在复平面上的观察,我们可以将单位根 \omega_n^{k} 写作
\omega_n^{k}=\cos k \frac{2\pi}{n} + i \sin k \frac{2\pi}{n}
时域和频域
还是稍微提一点信号相关的内容吧,原本不想从信号与系统开始讲的。
时域和频域就感性理解一下吧,对于一段音乐,我们从时域来看,是这样的:
而我们从频域来看,是这样的:
(我找不到自己制的谱了,网上找了一个)
音乐在时域上是一个随着时间变化的震动,但到了频域上就成为了由一些音符组成的乐谱。
其实频域上的音乐更合理的解释可能是,这个音乐是由多少个什么音在什么位置以什么时长组成的,但是浓缩到一块,就是乐谱了。
消息、信息与信号
消息 人们常常把来自外界的各种报道统称为消息。接受到某个消息,会引起接收者的知识状态发生改变。知识状态改变的程度由该消息中所包含的信息量决定。
信息 是信息论的一个术语,通常把消息中有意义的内容称为信息。某事件发生的信息量可定义为
**信号** 信号是携带信息的独立变量的函数。信号的信息的一种物理体现,一般是随时间或位置变换的物理量。电信号的基本形式是随时间变化的电压或电流。
描述信号的常用方法:
- 在时域上变化的函数;
- 信号的图形表示(波形)。
“信号”与“函数”通常相同通用。
### 傅里叶变换
傅里叶变换是一种数学变换,用于分析不同频率成分在信号中的分布,也就是说,它可以把信号分解成一系列不同频率、不同振幅的正弦、余弦波之和,完成从时域到频域的转换。
我们发现,正弦波叠加能够叠出各种不同的波形,比如,矩形:

这次图真是我画的了。
当求和式中的上界趋近无穷时,这些正弦波能叠成一个标准的矩形波。
不仅仅是矩形,你能想到的任何波形都是可以如此方法用正弦波叠加起来的。
我们记每个不同频率的正弦波为一个频率分量,则这个矩形波就是由无穷多个频率分量组合而来的。
如果我们把第一个频率最低的频率分量看作“1”,我们就有了构建频域的最基本单元,我们称之为**基**。
正弦波就是一个圆周运动在一条直线上的投影。所以频域的基本单元也可以理解为一个始终在旋转的圆。
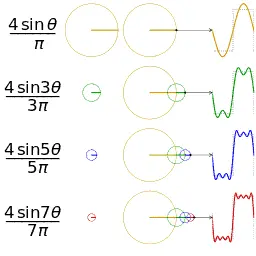
(图是从维基百科上贺的,懒得画了)
然后我们可以引入傅里叶变换了:
设 $f(t)$ 是关于时间 $t$ 的函数,即信号,傅里叶变换可以检测频率 $\omega$ 的周期在 $f(t)$ 出现的程度,也就是在整个时间范围内,频率为 $\omega$ 的正弦-余弦分量对信号 $f(t)$ 的整体贡献,有
$$F(\omega)=\mathbb F[f(t)] = \int_{-\infty}^{\infty} f(t) e^{-i\omega t}\text d t$$
它的逆变换是
$$f(t)=\mathbb F^{-1}[F(\omega)]=\frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{i\omega t}\text d \omega$$
注意到分解的时有复指数函数 $e^{i\omega t}$,这个便是分解的基函数。
傅里叶变换可以看作一个投影过程,把信号 $f(t)$ 投影到一系列代表不同频率的“基函数”上,这个基函数就是复正弦波 $e^{i\omega t}$。
我们可以将指数复变函数转化为三角函数形式,即
$$e^{-i\omega t}=\cos (\omega t)-i \sin(\omega t)$$
将上式代入傅里叶变换,得到
$$F(\omega)=\mathbb F[f(t)] = \int_{-\infty}^{\infty} f(t)(\cos (\omega t)-i \sin(\omega t) )\text d t$$
也就是说,傅里叶变换其实是将信号和复数信号做乘法后积分,得出信号与某一频率的复正弦波的相关度。
不难看出,傅里叶变换的结果是复数信号,其结果实部的值就是表示未知信号与 $\cos$ 信号的相关度,虚部值表示未知信号与 $\sin$ 信号的相关度。
### 离散傅里叶变换(DFT)
上述傅里叶变换是在时域和频域上连续的,而离散傅里叶变换,顾名思义,在时域和频域上均离散。
~~我这个概率论一点不会的人都知道~~,连续时积分,离散时求和。设 $\{x_n\}_{n=0}^{N-1}$ 是某一满足有限性条件的序列,将积分式略加修改,得到和式
$$X_k=\sum_{n=0}^{N-1}x_n e^{-i \frac{2\pi}{N} kn}$$
这个就是 $\{x_n\}$ 的**离散傅里叶变换**(DFT)。
同样地,我们可以写出它的逆变换(IDFT)
$$x_n=\frac{1}{N}\sum_{k=0}^{N-1}X_k e^{i \frac{2\pi}{N} kn}$$
变换式中的归一化系数,即 DFT 中的 $1$(被省略)和 IDFT 中的 $\frac{1}{N}$,并不是很重要,我们是可以把这个系数改成别的的,例如 $\frac{1}{\sqrt{N}}$ 和 $\frac{1}{\sqrt{N}}$。
离散傅里叶变换仍旧是时域到频域的变换。由于求和形式的特殊性,可以有其他的解释方法。
我们考虑把序列 $\{x_n\}$ 看作多项式 $f(x)$ 的 $x^n$ 项系数,则计算得到的变换 $X_k$ 恰好是多项式 $f(x)$ 代入 $e^{-i\frac{2k\pi}{N}}$ 的点值 $f(e^{-i\frac{2k\pi}{N}})$。
也就是说,DFT 是**将系数表达转换为点值表达**,IDFT 反之。
我们惊喜地发现,点值表达是可以直接做相乘的,例如,我们现在有一个 $n$ 次多项式 $f(x)$ 和一个 $m$ 次多项式 $g(x)$ 的点值表达
$$\{(x_1,y_1),(x_2,y_2),\dots,(x_{n+1},y_{n+1})\},\\
\{((a_1,b_1),(a_2,b_2),\dots,(a_{m+1}b_{m+1}))\}
$$
至于为什么是 $n+1$ 和 $m+1$ 个点,上一篇已经说明(拉格朗日插值法得出多项式的唯一性,即 $n+1$ 个点确定一个 $n$ 次多项式)。
如果我们想要确定一个 $n+m$ 次多项式,即它们的乘积 $f(x)g(x)$,需要 $n+m+1$ 个点,我们将两个序列补齐,有
$$\{(x_1,y_1),(x_2,y_2),\dots,(x_{n+m+1},y_{n+m+1})\},\\
\{((a_1,b_1),(a_2,b_2),\dots,(a_{n+m+1}b_{n+m+1}))\}
$$
将其相乘得到
$$\{(x_1a_1,y_1b_1),(x_2a_2,y_2b_2),\dots,(x_{n+m+1}a_{n+m+1},y_{n+m+1}b_{n+m+1})\},\\
$$
我们发现这就是 $f(x) \cdot g(x)$ 的点值表示,这样做的正确性是显然的。
接下来我们就可以直接通过 IDFT 将其转回系数表示。
但是我们发现系数转点值直接代入自然数是 $O(n^2)$ 的,似乎行不通,但是 DFT 中的 $e^{-i \frac{2k\pi}{N}}$ 告诉我们,这个复平面上的 $e$ 换成单位根是很有前途的。我们发现它就是 $N$ 次单位根 $\omega_N^{k}$。也就是说,DFT 完成了一个代入单位根求点值的过程。
接下来就简单了,我们只需要考虑优化代入单位根求点值的过程。
### 快速傅里叶变换(FFT)
考虑分治。对于一个多项式 $F(x)$,我们把奇数次项和偶数次项分开,得到两个多项式
$$\begin{aligned}
G(x)&=\sum_{0\le k \le n, 2\mid k}[x^k]f(x)x^{\frac{k}{2}} \\
H(x)&=\sum_{0\le k \le n,2\nmid k} [x^k]f(x)x^{\frac{k-1}{2}}
\end{aligned}$$
于是 $F(x)=G(x^2)+xH(x^2)$,代入单位根 $\omega_n^k$ 和 $\omega_n^{k+\frac{n}{2}}$,我们可以得到
$$\begin{aligned}
F(\omega_n^k)&=G((\omega_n^k)^2)+\omega_n^k H((\omega_n^k)^2)\\
F(\omega_n^{k+\frac{n}{2}})&=G((\omega_n^{k+\frac{n}{2}})^2)+\omega_n^{k+\frac{n}{2}} H((\omega_n^{k+\frac{n}{2}})^2)
\end{aligned}$$
至于化简,想象一下复平面上一条射线转来转去即可。
我们得到
$$\begin{aligned}
F(\omega_n^k)&=G(\omega_{\frac{n}{2}}^k)+\omega_n^k H(\omega_{\frac{n}{2}}^k)\\
F(\omega_n^{k+\frac{n}{2}})&=G(\omega_{\frac{n}{2}}^k)-\omega_n^k H(\omega_{\frac{n}{2}}^k)
\end{aligned}$$
如此递归下去,时间复杂度 $O(n\log n)$。
我们考虑把点值转回多项式,显然可以直接 IDFT,也把式子中 $e$ 的幂次换成单位根,不做赘述。
当然我们发现这个过程要求 $G(x)$ 和 $H(x)$ 等长,这个不难,将长度补齐到最小的大于等于它的幂次即可。
我们发现常数已经大上天了。
如果我们不选择递归实现,可以减小很多常数。
因此,考虑先把每一位交换到它最后会在的地方,然后向上归并实现。考虑每一位最后会到哪里。若当前最低位为 $0$,则变换后它会到前一半,否则会到后一半。显然就是 $2$ 进制下翻转了一下。可以递推求出。然后我们只需枚举当前的区间长度($2,4,8,\dots$),并枚举区间,用上面的式子计算就行了。
显然 DFT 和 IDFT 形式差不多,我们可以将两个函数封装在一起,IDFT 取另一半的单位根,且最后要除掉 $n$。
其实我们可以进一步优化。我们发现上面操作需要 $2$ 次 DFT 和 $1$ 次 IDFT,其实我们可以减少一次 DFT。
我们将两个多项式的系数分别放到复系数的实部和虚部,做一次自卷积即可。
我们说的卷积,即对于多项式 $F(x)$ 和 $G(x)$,其卷积为
$$(F*G)(n) = \sum_i F(i) G(n-i)$$
而自卷积显然少了一次对另一个多项式的 DFT,成功减小了常数。
:::info[代码实现(P3803,倍增 FFT)]
```cpp
#include <bits/stdc++.h>
#define pi acos(-1.0)
using namespace std;
namespace fft
{
template<typename _Tp=double>
class fcomplex
{
public:
_Tp x,y;
fcomplex(_Tp X=0,_Tp Y=0) : x(X),y(Y) {}
inline fcomplex<_Tp> operator+(const fcomplex<_Tp> b) const {return fcomplex(this->x+b.x,this->y+b.y);}
inline fcomplex<_Tp> operator-(const fcomplex<_Tp> b) const {return fcomplex(this->x-b.x,this->y-b.y);}
inline fcomplex<_Tp> operator*(const fcomplex<_Tp> b) const {return fcomplex(this->x*b.x-this->y*b.y,this->x*b.y+this->y*b.x);}
inline fcomplex<_Tp> operator*(const _Tp b) const {return fcomplex(this->x*b,this->y*b);}
inline fcomplex<_Tp> operator/(const _Tp b) const {return fcomplex(this->x/b,this->y/b);}
inline fcomplex<_Tp>& operator+=(const fcomplex<_Tp> b) {this->x+=b.x;this->y+=b.y;return *this;}
inline fcomplex<_Tp>& operator-=(const fcomplex<_Tp> b) {this->x-=b.x;this->y-=b.y;return *this;}
inline fcomplex<_Tp>& operator*=(const fcomplex<_Tp> b) {fcomplex<_Tp> tmp=(*this)*b;this->x=tmp.x;this->y=tmp.y;return *this;}
inline fcomplex<_Tp>& operator*=(const _Tp b) {this->x*=b;this->y*=b;return *this;}
inline fcomplex<_Tp>& operator/=(const _Tp b) {this->x/=b;this->y/=b;return *this;}
};
template<typename _Tp=double>
void FFT(fcomplex<> a[],int rv[],_Tp type,int lim)
{
for(int i=1;i<=lim;i++)
if(i<rv[i])
swap(a[i],a[rv[i]]);
fcomplex<> k,x,y,tmp;
for(int mid=1;mid<lim;mid<<=1)
{
int r=(mid<<1);
k=fcomplex<>(cos(pi/mid),type*sin(pi/mid));
for(int j=0;j<lim;j+=r)
{
tmp=fcomplex<>(1,0);
for(int t=0;t<mid;t++)
{
x=a[j|t];
y=tmp*a[j|t|mid];
a[j|t]=x+y;
a[j|t|mid]=x-y;
tmp*=k;
}
}
}
if(type==1)
return;
for(int i=0;i<=lim;i++)
a[i]/=1.0*lim;
}
};
int n,m,lim=1,l=-1;
int rev[4000005];
fft::fcomplex<> f[4000005];
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++)
{
int tmp;
scanf("%d",&tmp);
f[i].x=tmp;
}
for(int i=0;i<=m;i++)
{
int tmp;
scanf("%d",&tmp);
f[i].y=tmp;
}
while(lim<=n+m)
{
lim<<=1;
l++;
}
for(int i=1;i<=lim;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<l);
FFT(f,rev,1,lim);
for(int i=0;i<=lim;i++)
f[i]*=f[i];
FFT(f,rev,-1,lim);
for(int i=0;i<=n+m;i++)
printf("%d ",int(f[i].y/2+0.5));
printf("\n");
return 0;
}
```
:::
### 快速数论变换(NTT)
NTT 和 FFT 是本质相同的,但是顾名思义,数论变换,一定是用到了数论相关的内容。具体用到了什么,答案是**原根**。
FFT 需要浮点数运算和复数运算,不仅有精度误差,还很慢。而且我们很多时候需要求出模意义下的结果。
我们考虑使用与单位根性质相似的数论内容代替单位根。我们发现原根满足这一点,对于一个奇质数 $p$ 的原根 $g$,有 $g^k \equiv 1$ 且 $k$ 最小。为了使之能充当单位根并继续使用基于分治思想的 DFT,我们需要让 $k$ 是 $2$ 的幂次且尽可能大。我们把这样的模数 $p$ 称为 NTT 模数,它们都可以写成 $a2^b+1$ 的形式,例如 $998244353=7 \times 17 \times 2^{23}+1$,其最小原根为 $3$。
我们稍微改动一下 FFT,便可以得到 NTT。
:::info[代码实现(P3803,NTT)]
~~附赠了一个老版 wyzfastio。~~
```cpp
#include <bits/stdc++.h>
//#include <bits/extc++.h>
namespace wyzfastio
{
#define usefio
#ifdef usefio
namespace __getchar{const int bufsize=1<<20;char buf[bufsize<<1],*p1=buf,*p2=buf;inline char getchar(){return (p1==p2&&(p2=(p1=buf)+fread(buf,1,bufsize,stdin),p1==p2))?EOF:(*p1++);}}using __getchar::getchar;
namespace __putchar{const int bufsize=1<<20;char buf[bufsize<<1],*p=buf;inline void putchar(const char ch){if(p-buf==bufsize) fwrite(buf,1,bufsize,stdout),p=buf;*p++=ch;}inline void flush(){fwrite(buf,1,p-buf,stdout);}}using __putchar::putchar;using __putchar::flush;
namespace __flusher{struct Flusher{Flusher(){}~Flusher(){flush();}}flusher;}
#endif
/*---input---*/
inline void read(unsigned long long &x){char ch=getchar();unsigned long long res=0;while(ch<'0'||ch>'9')ch=getchar();while(ch>='0'&&ch<='9')res=(res<<3)+(res<<1)+ch-'0',ch=getchar();x=res;}
inline void read(unsigned int &x){char ch=getchar();unsigned int res=0;while(ch<'0'||ch>'9')ch=getchar();while(ch>='0'&&ch<='9')res=(res<<3)+(res<<1)+ch-'0',ch=getchar();x=res;}
inline void read(long long &x){char ch=getchar();long long f=1;unsigned long long res=0;while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}while(ch>='0'&&ch<='9')res=(res<<3)+(res<<1)+ch-'0',ch=getchar();x=res*f;}
inline void read(int &x){char ch=getchar();int f=1;unsigned res=0;while(ch<'0'||ch>'9'){if(ch=='-')f=-f;;ch=getchar();}while(ch>='0'&&ch<='9')res=(res<<3)+(res<<1)+ch-'0',ch=getchar();x=res*f;}
inline void read(char &s){s=getchar();while(s==' '||s=='\n'||s=='\r') s=getchar();}
inline int read(char *s){int i=0;char ch=getchar();while(ch==' '||ch=='\n'||ch=='\r') ch=getchar();while(!(ch==' '||ch=='\n'||ch=='\r'||ch==EOF)) s[++i]=ch,ch=getchar();s[i+1]='\0';return i;}
inline void read(std::string &s){char ch=getchar();s.clear();while(ch==' '||ch=='\n'||ch=='\r') ch=getchar();while(!(ch==' '||ch=='\n'||ch=='\r'||ch==EOF)) s.push_back(ch),ch=getchar();}
template<typename _Tp,typename ...Args>inline void read(_Tp &x,Args &...args){read(x),read(args...);}
/*---output---*/
inline void write(const unsigned long long x){if(x<10) putchar(x+'0');else write(x/10),putchar(x%10+'0');}
inline void write(const long long x){unsigned long long t=x;if(x<0)putchar('-'),t=-x;write(t);}
inline void write(const unsigned int x){if(x<10) putchar(x+'0');else write(x/10),putchar(x%10+'0');}
inline void write(const int x){unsigned int t=x;if(x<0)putchar('-'),t=-x;write(t);}
inline void write(const char x){putchar(x);}
inline void write(const char *s){while(*s!='\0'&&*s!=EOF)putchar(*s),s++;}
template<typename _Tp,typename ...Args>inline void write(_Tp x,Args ...args){write(x),write(args...);}
}
//#define int long long
#define mod 998244353
#define G 3
#define invG 332748118
#define N 4000005
#define __BEGIN_MULTITEST__ \
signed T; \
cin>>T; \
while(T--) \
{
#define __END_MULTITEST__ }
using namespace std;
using namespace wyzfastio;
//using namespace __gnu_cxx;
//using namespace __gnu_pbds;
int rev[N];
inline int quick_pow(int a,int b)
{
int ret=1;
while(b)
{
if(b&1)
ret=1ll*ret*a%mod;
a=1ll*a*a%mod;
b>>=1;
}
return ret;
}
int lim=1;
int n,m;
int f[N],g[N];
signed main()
{
// cin.tie(nullptr)->sync_with_stdio(false);
// __BEGIN_MULTITEST__
auto NTT=[&](int *f,const int type)
{
for(int i=1;i<=lim;i++)
if(i<rev[i])
swap(f[i],f[rev[i]]);
for(int k=1;(k<<1)<=lim;k<<=1)
for(int i=0,w=quick_pow(type==1?G:invG,(mod-1)/(k<<1));i<lim;i+=(k<<1))
for(int j=0,prodw=1;j<k;j++,prodw=1ll*prodw*w%mod)
{
int x=f[i|j],y=1ll*prodw*f[i|j|k]%mod;
f[i|j]=x+y-(x+y>=mod)*mod;
f[i|j|k]=x-y+(x-y<0)*mod;
}
if(type==-1)
{
int tmpinv=quick_pow(lim,mod-2);
for(int i=0;i<=lim;i++)
f[i]=1ll*f[i]*tmpinv%mod;
}
};
read(n,m);
for(int i=0;i<=n;i++)
read(f[i]);
for(int i=0;i<=m;i++)
read(g[i]);
lim=1<<__lg(n+m)+1;
for(int i=0;i<=lim;i++)
rev[i]=(rev[i>>1]>>1)|(i&1?lim>>1:0);
NTT(f,1);
NTT(g,1);
for(int i=0;i<=lim;i++)
f[i]=1ll*f[i]*g[i]%mod;
NTT(f,-1);
for(int i=0;i<=n+m;i++)
write(f[i],' ');
write('\n');
// __END_MULTITEST__
return 0;
}
```
:::
有了 NTT,我们就可以获得多项式全家桶,当然这是后话了。
## 拉格朗日插值
~~上一篇的某个定理名称为这篇中的两个老人插值的出现埋下了伏笔。~~
对于平面上的 $n$ 个点,如下图,我们可以用线性分段函数来拟合,

图中所示函数为
$$f(x)=\begin{cases}
2x-1,&x\le2 \\
-8x+19,&2\le x\le3 \\
5x-20,&3\le x\le4 \\
-x+4,&x\ge 4
\end{cases}$$
也可以用多项式来拟合,

图中所示函数为
$$f(x)=-\frac{7}{4}x^{4}+\frac{64}{3}x^{3}-\frac{357}{4}x^{2}+\frac{440}{3}x-76$$
我们称之为多项式插值。
也就是说,我们现在需要构造一个多项式 $f(x)$ 过点 $P_1(x_1,y_1),P_2(x_2,y_2),\dots,P_n(x_n,y_n)$。为了简便,我们限定多项式的次数 $\le n+1$,于是结果的唯一性已经确定,证明见上一篇中“拉格朗日插值得出多项式的唯一性”。
~~很简单所以贺了 OI Wiki。~~
我们设第 $i$ 个点 $P_i$ 在 $x$ 轴上的投影为 $P_i'(x_i,0)$。
我们构造 $n$ 个函数 $f_1(x),f_2(x),\dots,f_n(x)$,使得第 $i$ 个函数 $f_i(x)$ 过点 $P_i$ 和所有满足 $j\ne i$ 的 $P_j'$,由题意,$f(x)=\sum_{i=1}^n f_i(x)$。
设 $f_i(x)=a\prod\limits_{j\ne i} (x-x_j)$,将点 $P_i$ 代入得 $a=\dfrac{y_i}{\prod\limits_{j\ne i}(x_i-x_j)}$,故
$$f_i(x)=y_i\prod_{j\ne i} \frac{x-x_j}{x_i-x_j}$$
对 $f_i(x)$ 求和即得 $f(x)$。
时间复杂度 $O(n^2)$,当然,我们可以使用 FFT 优化这一过程至 $O(n\log^2 n)$,但是需要用到多点求值,就先不讲了。