题解:P13976 数列分块入门 1
Lonelyhacker
·
·
题解
前日谈
无意倒序排序洛谷主题库题目,看到竟有此题,大喜,将 LOJ 的代码直接 copy,WA,大惊。
刚想在 CSP 考试前复习一下分块,就看到这道题,挺好的。
题意
给出一个长为 n 的数列,以及 n 个操作,操作有两种(\mathrm{opt}\in\{0,1\}),涉及:
- 区间加(\mathrm{opt}=0),令 \forall i \in [l,r],a_i \leftarrow a_i+c。
- 单点查询(\mathrm{opt}=1),询问 a_r 的值。
## 题解
#### Part 1. 分块的原理
此部分仅对分块 $0$ 基础的小朋友,dalao 们可以跳过这部分。
分块顾名思义,就是将序列(或者别的)分成 $\sqrt{n}$ 个长度为 $\sqrt{n}$ 的块。修改时若可能,整块地修改,否则散块(散点)单独修改。换种说法,能打懒标记就打,否则直接暴力修改。查询同理。
记住,**一般情况下**,带 $\log$ 的复杂度是比带根号的要优秀得多的,除非题目有特殊性质或者数据精心构造(~~点名“云南” OI~~),否则能用带 $\log$ 的数据结构或算法就用。
分块作用一般是:
1. 平衡时间复杂度。有时候修改次数少,询问次数多(或反之),可以设计使得操作次数多的那一项的复杂度变成 $O(1)$ 的,另一个为 $O(\sqrt{n})$。有些时候(比如题目特别说明操作次数仅有 $100$ 次这种)比常规的,两种操作都是 $O(\log n)$ 的算法(数据结构)要好一些。
2. 维护一些正常带 $\log$ 的数据结构不能维护的数据等。
我们用图讲解一下分块的具体做法:
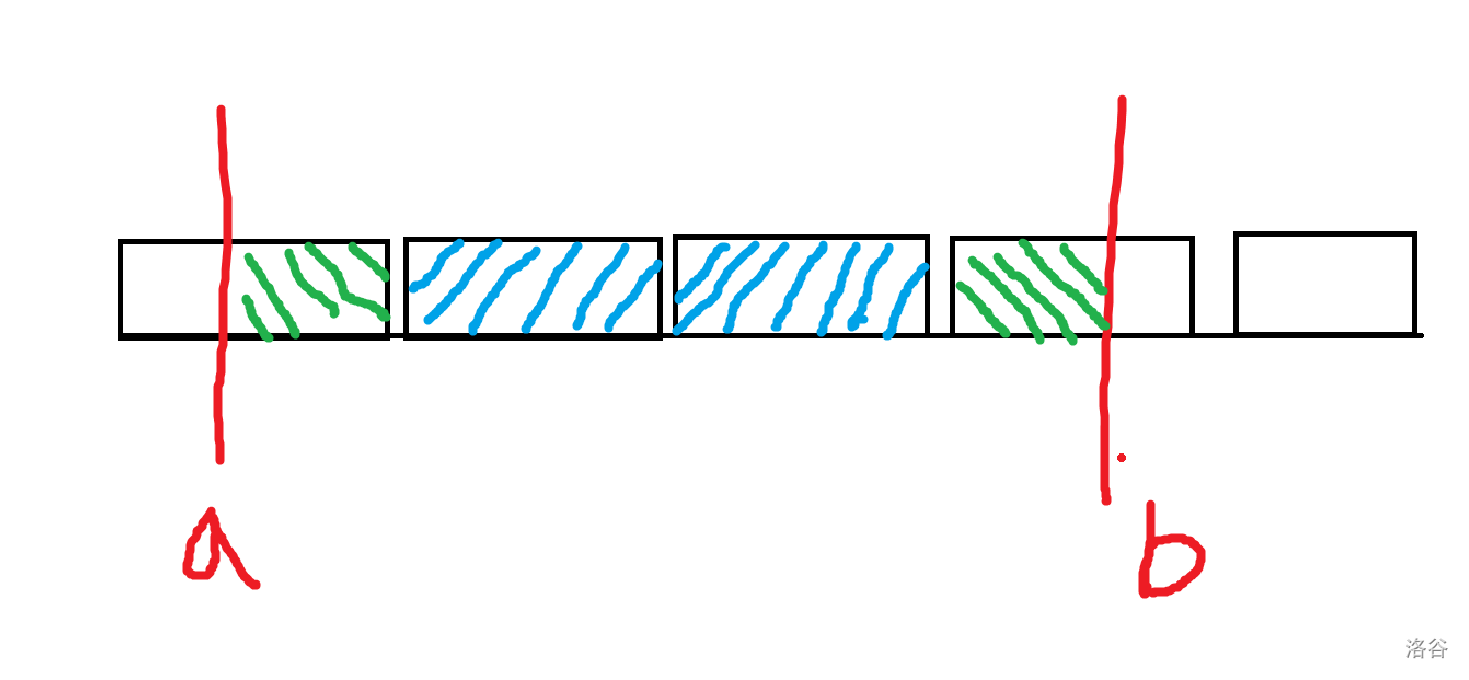
如图,假设我们已经将一个序列分成图中的 $5$ 个块,我们要将区间 $[a,b]$ 中的元素增加某个值 $c$。比较一般的情况就是上图,$a,b$ 中有蓝色的整块,以及绿色的散块(散点)。遇到整块,我们直接用懒标记,给整块的修改量增加 $c$。遇到散块(散点),我们直接给其值加上 $c$,即暴力修改。由于我们的块长为 $\sqrt{n}$,即分了 $\sqrt{n}$ 个块,区间一次修改最多对 $\sqrt{n}$ 个整块进行修改,而对于散块(散点)而言,其长度也严格小于 $\sqrt{n}$(否则就变成新的整块了),因此单次修改是 $\sqrt{n}$ 的。而对于查询,我们让其本身的值加上其所在块的懒标记,就是最终结果,而这是 $O(1)$ 的。总共 $n$ 个操作,时间复杂度为 $O(n\sqrt{n})$。
代码实现层面有很多中写法,此处我介绍我的:开一个数组 `bl[i]` 表示下标 $i$ 所在的块的编号,`v[i]` 表示 $a_i$,`blo` 表示每个块的块长。对于左右两边的散块暴力处理:找到 $a$ 所在的块的编号即 `bl[a]`,再乘上块长 `blo` 就是这个块的右端点,将散块(散点)$[a,bl_a\times blo]$ 都加上 $c$;$b$ 所在散块同理,但是我们要求 `bl[b]` 的左端点而非右端点,怎么办?简单,`bl[b]` 的上一个块的右端点 $+1$ 不就是当前块的左端点了?其中间的整块就是 $[bl_a+1,bl_b-1]$ 这部分,给这些整块的懒标记加 $c$ 即可。
这只是一般的情况,实际上可能出现这种:
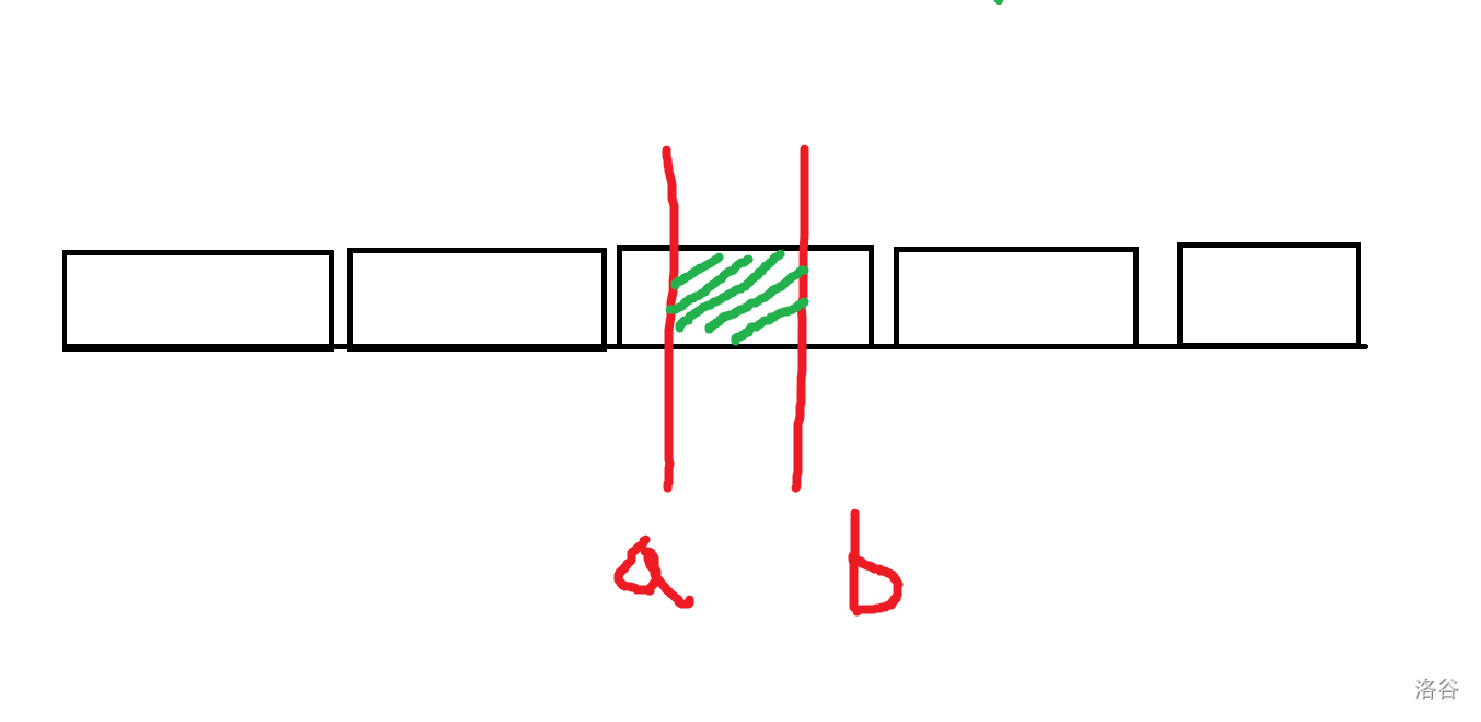
如图,$a,b$ 都在同一个块内,没有整块只有散块(散点)。如果还按照刚刚的做法,那么处理散块(散点)的时候,$a$ 所在的散块(散点)与 $b$ 所在的散块(散点)是同一个块,就会重复累加。因此,我们还需要特判 `bl[a] == bl[b]`,即 $a,b$ 在同一个块的情况。
而且此时,显然 $a$ 所在的散块(散点)的右端点并非 $a$ 所在块的右端点,而是 $b$,因此在代码里我们还要加一些特判。
分块的思想差不多就是这样,分成整块和散块(散点)分别处理,然后注意一些细节上的东西即可。
至于块长,一般是取 $\sqrt{n}$ 的,但题目有些卡常的时候可以手动改一下块长,例如直接给定一个常数 $100\sim300$ 这种,有时候很管用,但不适合用根号做的题目就不要妄想这样能卡过了,老老实实用 $\log$ 和线性的算法吧。
#### Part 2. 此题做法
话说我们上面已经基本将正解说出来了,那为了给会分块,跳过了上面部分的 dalao 们讲解,我们做一个总结:
1. 修改操作。整块用懒标记,散块(散点)暴力修改,直接在原值上操作。注意特判没有整块,或者说左右端点在同一个块内的情况。
2. 查询单点。直接输出该点的值与其所在块的懒标记的和。
很简单,直接放代码吧。
## 代码
保留注释,供不明所以之人查阅之用。
```cpp
#include <iostream>
#include <cmath>
using namespace std;
const int N = 3e5+5;
typedef long long ll;
int n, blo;
// bl[i]:元素i属于哪个块
// atag:加法的懒标记
int bl[N];
ll v[N], atag[N];
void add(int a, int b, ll c){
// 暴力处理左边的散块
for (int i = a; i <= min(bl[a]*blo, b); i++) // 这里的min是看右边界是在块a的右边界还是在b,至于为什么是b看下面
v[i] += c;
// 这里若没有特判a,b不在同一散块,会执行两次
if (bl[a] != bl[b]) // 执行两次即下文代码效果与上文一样
for (int i = (bl[b]-1)*blo+1; i <= b; i++) // 这里就是从b所在块的左边一个块的右边界的下一个元素开始,一直到b
v[i] += c; // 暴力处理右边的散块
for (int i = bl[a]+1; i <= bl[b]-1; i++) // 处理夹在a与b之间的整块们
atag[i] += c; // 处理整块
}
int main(){
ios::sync_with_stdio(0); cin.tie(0);
cin >> n;
blo = sqrt(n); // 块长
for (int i = 1; i <= n; i++) cin >> v[i];
for (int i = 1; i <= n; i++)
bl[i] = (i-1)/blo+1; // 获取块
for (int i = 1, f, a, b; i <= n; i++){
ll c;
cin >> f >> a >> b >> c;
if (f == 0) add(a, b, c);
else cout << v[b]+atag[bl[b]] << '\n';
// 其本身值+其所在分块的变化值
}
return 0;
}
```
## 后日谈
本人第一篇黄题题解。