NOI 2014 消除游戏 全网第二发题解
ix35
·
·
题解
NOI 2014 消除游戏
今天与这题大战半天,做之前没有在网上看到任何一篇这题的题解,做完之后才发现 UOJ 上有人写过博客,不过百度上也搜不到,所以我来写一下。
题目大意:
这是一道提交答案题。
给定 n\times m 网格,网格中的数都是 [0,9] 的整数。
每轮你可以选择一条简单路径,满足路径上每个格子都有数,且起始点的数不为 0。设你的路径长度为 l,路径上的数顺次构成一个整数 X:
- 如果 X 是素数,则你的素数加分为 l^{c_1},否则素数加分为 1;
- 如果 X 是回文数,则你的回文加分为 l^{c_2},否则回文加分为 1。
这轮操作的总分是素数加分和回文加分的和。但是特别地,如果 X 既不是素数又不是回文数,则这个操作非法。
每轮操作结束后,路径上的所有数会消失,然后网格中所有数按重力规则下落。
你最多可以进行 K 轮上述操作,并且每次的路径长度 l 需要满足 l_{min}\leq l\leq l_{max}。
此外有一个参数 F,如果 F=0,则你的总分等于每轮操作总分之和;如果 F=1,则再设 d 是操作结束后网格中剩下的数的个数,你的总分等于每轮操作的总分之和除以 2^d 下取整。你要构造一个方案使得总分足够大(有一些不告诉你的评分参数)。
每个测试点给定的东西包括 n,m,K,l_{min},l_{max},c_1,c_2,F 和初始的网格。
测试点 1:
```
1 1 2 3 4
0 1 2 3 5
0 6 5 4 6
0 7 8 8 7
0 0 0 0 7
```
我们发现右上角 $4\times 4$ 的块正好可以构成一个长度为 $16$ 的回文数 $1234567887654321$,而左下这一条是一个素数 $10^8+7$。
于是分成这两部分,可以通过该测试点。
---
### 测试点 2:
$n=m=10,\ K=100,\ l_{min}=2,\ l_{max}=8,\ c_1=c_2=1,\ F=1$,网格如下:
```
7 4 1 3 5 9 8 6 1 6
8 0 9 1 1 1 1 7 1 2
9 3 6 7 5 1 5 9 6 0
8 1 8 4 9 7 7 4 3 9
0 4 0 0 9 0 1 7 8 3
8 4 8 7 3 7 8 0 7 0
7 1 6 6 1 0 5 8 9 0
5 9 9 1 1 5 1 5 1 5
8 1 2 7 6 2 3 3 3 0
0 9 1 0 9 4 0 6 1 9
```
我们发现由于 $F=1$,所以关键在于要把所有数消除光。
可以写个暴力 DFS:每次随机一个起点,然后随机一条从它开始的简单路径,然后检验是否合法,如果合法就删除后递归。如果某个 DFS 分支已经走不下去了就回溯,只要记下之前的地图就可以轻易地完成回溯操作。
这个做法搜出的解大概可以得到 $[7,9]$ 分。
我们可以加个优化:只使用长度 $\leq 4$ 的路径,因为长度越小能蹭到的分数 $1$ 就越多,所以这样总分会稍微大一些,可以通过该测试点。
```cpp
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=110;
int n,m,k,l1,l2,c1,c2,f,mp[N][N],vis[N][N],dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
vector < pair<int,int> > v;
vector < vector < pair<int,int> > > ans;
ull sd;
ull rd () {sd^=(sd<<27);sd^=(sd>>19);sd^=(sd<<25);return sd;}
ll qmul (ll a,ll b,ll p) {return (a*b-(ll)((long double)a/p*b)*p+p)%p;}
ll qpow (ll a,ll b,ll p) {
ll res=1;
while (b) {
if (b&1) {res=qmul(res,a,p);}
a=qmul(a,a,p),b>>=1;
}
return res;
}
bool mr (ll p,ll x) {
if (qpow(x,p-1,p)!=1) {return 0;}
ll k=p-1;
while (!(k&1)) {
k>>=1;
ll tmp=qpow(x,k,p);
if (tmp==p-1) {return 1;}
else if (tmp!=1) {return 0;}
}
return 1;
}
bool isp (ll p) {
if (p==46856248255981||p==1) {return 0;}
if (p==2||p==3||p==7||p==61||p==24251) {return 1;}
return mr(p,2)&&mr(p,3)&&mr(p,7)&&mr(p,61)&&mr(p,24251);
}
bool chk (int x,int y) {return (x>0&&y>0&&x<=n&&y<=m&&mp[x][y]!=-1&&!vis[x][y]);}
void sr () {
int x=rd()%n+1,y=rd()%m+1,cc=0;
while (mp[x][y]<=0&&cc<=200) {x=rd()%n+1,y=rd()%n+1,cc++;}
if (mp[x][y]<=0) {return;}
v.push_back(make_pair(x,y));vis[x][y]=1;
for (int i=1;i<=4;i++) {
int dr=rd()%4;
for (int i=1;i<=4;i++) {
if (!chk(x+dir[dr][0],y+dir[dr][1])) {dr=(dr+1)%4;}
}
if (!chk(x+dir[dr][0],y+dir[dr][1])) {break;}
x+=dir[dr][0],y+=dir[dr][1];
v.push_back(make_pair(x,y));vis[x][y]=1;
}
for (auto x:v) vis[x.first][x.second]=0;
}
bool chkk () {
ll tmp=0;
if (v.size()<=1) {return 0;}
for (auto x:v) {tmp=tmp*10+mp[x.first][x.second];}
int flg=1,len=v.size();
for (int i=0;i<len;i++) {if (mp[v[i].first][v[i].second]!=mp[v[len-i-1].first][v[len-i-1].second]) flg=0;}
//if (isp(tmp)||flg) cerr << tmp << endl;
return isp(tmp)||flg;
}
void drp () {
for (auto x:v) {mp[x.first][x.second]=-1;}
for (int j=1;j<=m;j++) {
int cnt=n;
for (int i=n;i>=1;i--) {
if (mp[i][j]!=-1) {mp[cnt--][j]=mp[i][j];}
}
while (cnt) {mp[cnt--][j]=-1;}
}
}
bool dfs (int d) {
int tmp[11][11],flg=0;
for (int i=1;i<=10;i++) {
for (int j=1;j<=10;j++) {flg|=(mp[i][j]>=0);tmp[i][j]=mp[i][j];}
}
if (!flg) {return 1;}
for (int i=1;i<=200/d;i++) {
v.clear();
sr();
if (chkk()) {
ans.push_back(v);
drp();
if (dfs(d+1)) {return 1;}
ans.pop_back();
for (int i=1;i<=10;i++) {
for (int j=1;j<=10;j++) {mp[i][j]=tmp[i][j];}
}
}
}
return 0;
}
int main () {
freopen("game2.in","r",stdin);
freopen("game2.out","w",stdout);
srand(time(0));
sd=rand()+1;
scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
for (int i=1;i<=n;i++) {
for (int j=1;j<=m;j++) {scanf("%d",&mp[i][j]);}
}
cerr << dfs(1) << endl;
printf("%d\n",ans.size());
for (auto v:ans) {
printf("%d ",v.size());
for (auto x:v) {printf("%d %d ",x.first,x.second);}
printf("\n");
}
return 0;
}
```
---
### 测试点 3:
$n=m=100,\ K=500,\ l_{min}=2,\ l_{max}=18,\ c_1=2,\ c_2=0,\ F=0$,网格随机。
我们发现,想要得到最大的分数,只需要每次选出的都是一个 $18$ 位素数即可,由于素数密度是 $1/\ln n$ 级别,所以只要每次暴力随机一条路径,用 MR 判一下是不是素数就可以了,$500\times 18=9000$,比 $10000$ 小不少,可以轻松出解。
---
### 测试点 4:
$n=m=100,\ K=500,\ l_{min}=15,\ l_{max}=18,\ c_1=2,\ c_2=0,\ F=0$,网格随机。
同测试点 3,以下是这两个点的程序。
```cpp
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=110;
int n,m,k,l1,l2,c1,c2,f,mp[N][N],vis[N][N],dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
vector < pair<int,int> > v;
ull sd;
ull rd () {sd^=(sd<<27);sd^=(sd>>19);sd^=(sd<<25);return sd;}
ll qmul (ll a,ll b,ll p) {return (a*b-(ll)((long double)a/p*b)*p+p)%p;}
ll qpow (ll a,ll b,ll p) {
ll res=1;
while (b) {
if (b&1) {res=qmul(res,a,p);}
a=qmul(a,a,p),b>>=1;
}
return res;
}
bool mr (ll p,ll x) {
if (qpow(x,p-1,p)!=1) {return 0;}
ll k=p-1;
while (!(k&1)) {
k>>=1;
ll tmp=qpow(x,k,p);
if (tmp==p-1) {return 1;}
else if (tmp!=1) {return 0;}
}
return 1;
}
bool isp (ll p) {
if (p==46856248255981||p==1) {return 0;}
if (p==2||p==3||p==7||p==61||p==24251) {return 1;}
return mr(p,2)&&mr(p,3)&&mr(p,7)&&mr(p,61)&&mr(p,24251);
}
bool chk (int x,int y) {return (x>0&&y>0&&x<=n&&y<=m&&mp[x][y]!=-1&&!vis[x][y]);}
void sr () {
int x=rd()%n+1,y=rd()%m+1;
while (mp[x][y]<=0) {x=rd()%n+1,y=rd()%n+1;}
v.push_back(make_pair(x,y));vis[x][y]=1;
for (int i=1;i<=17;i++) {
int dr=rd()%4;
for (int i=1;i<=4;i++) {
if (!chk(x+dir[dr][0],y+dir[dr][1])) {dr=(dr+1)%4;}
}
if (!chk(x+dir[dr][0],y+dir[dr][1])) {break;}
x+=dir[dr][0],y+=dir[dr][1];
v.push_back(make_pair(x,y));vis[x][y]=1;
}
for (auto x:v) vis[x.first][x.second]=0;
}
bool chkk () {
ll tmp=0;
if (v.size()!=18) {return 0;}
for (auto x:v) {tmp=tmp*10+mp[x.first][x.second];}
cerr << tmp << endl;
return isp(tmp);
}
void drp () {
for (auto x:v) {mp[x.first][x.second]=-1;}
for (int j=1;j<=m;j++) {
int cnt=n;
for (int i=n;i>=1;i--) {
if (mp[i][j]!=-1) {mp[cnt--][j]=mp[i][j];}
}
while (cnt) {mp[cnt--][j]=-1;}
}
}
int main () {
freopen("game4.in","r",stdin);
freopen("game4.out","w",stdout);
srand(time(0));
sd=rand()+1;
scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
for (int i=1;i<=n;i++) {
for (int j=1;j<=m;j++) {scanf("%d",&mp[i][j]);}
}
for (int i=1;i<=k;i++) {
v.clear();
while (1) {
sr();
if (!chkk()) {v.clear();}
else {break;}
}
printf("%d ",v.size());
for (auto x:v) {printf("%d %d ",x.first,x.second);}
printf("\n");
drp();
}
return 0;
}
```
---
### 测试点 5:
$n=m=10,\ K=100,\ l_{min}=2,\ l_{max}=8,\ c_1=c_2=2,\ F=0$,网格如下:
```
9 0 4 4 4 0 1 0 0 9
4 3 4 1 5 3 3 6 2 2
6 9 8 0 4 9 9 1 7 7
5 3 2 5 6 8 0 5 8 0
1 7 4 5 0 7 0 5 7 3
5 3 5 1 0 9 7 2 3 4
3 6 3 9 4 5 2 6 4 5
9 7 6 5 5 1 6 6 3 0
9 3 1 0 7 6 8 3 2 2
9 0 9 4 8 4 4 5 0 6
```
和测试点 2 的区别是 $c=2$ 且 $F=0$,那么不用消完,但是需要尽可能消比较长的段,我们只需要在测试点 2 的爆搜中限制只搜长度等于 $8$ 的路径,就可以得到大概 $7$ 分到 $9$ 分。
搜出一个包含 $12$ 条长度为 $8$ 的路径的解,这时还剩 $4$ 个元素,如果运气好的话(多试几次)还能再找到一条长度为 $3$ 或者 $4$ 的路径,手动把它加上,就可以通过了。
---
### 测试点 6:
$n=m=1000,\ K=1,\ l_{min}=2,\ l_{max}=1000,\ c_1=0,\ c_2=1,\ F=0$,网格只包含 $1,2$,随机生成。
翻译一下,其实就是找到一条长度不超过 $1000$ 的尽量长的回文简单路径。
那么暴搜即可,每次随机一个中心,然后往两边扩展,很容易找到长度恰好为 $1000$ 的回文路径。
---
### 测试点 7:
$n=m=1000,\ K=1,\ l_{min}=2,\ l_{max}=1000,\ c_1=0,\ c_2=1,\ F=0$,网格只包含 $2,3,4$,随机生成。
同测试点 6,以下是这两个点的程序。
```cpp
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=1010;
int n,m,k,l1,l2,c1,c2,f,mp[N][N],vis[N][N],dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
vector < pair<int,int> > v1,v2;
ull sd;
ull rd () {sd^=(sd<<27);sd^=(sd>>19);sd^=(sd<<25);return sd;}
bool chk (int x,int y) {return (x>0&&y>0&&x<=n&&y<=m&&mp[x][y]!=-1&&!vis[x][y]);}
bool dfs (int x1,int y1,int x2,int y2,int v) {
//cout << x1 << " " << y1 << " " << x2 << " " << y2 << " " << v << endl;
v1.push_back(make_pair(x1,y1)),v2.push_back(make_pair(x2,y2));
vis[x1][y1]=vis[x2][y2]=1;
if (v==500) {return 1;}
for (int i=0;i<=3;i++) {
for (int j=0;j<=3;j++) {
int x3=x1+dir[i][0],y3=y1+dir[i][1],x4=x2+dir[j][0],y4=y2+dir[j][1];
if (chk(x3,y3)&&chk(x4,y4)&&mp[x3][y3]==mp[x4][y4]) {
if (dfs(x3,y3,x4,y4,v+1)) {return 1;}
}
}
}
v1.pop_back(),v2.pop_back();
vis[x1][y1]=vis[x2][y2]=0;
return 0;
}
bool solve () {
int x=rd()%n+1,y=rd()%m+1,d=rd()%4,x2=x+dir[d][0],y2=y+dir[d][1];
while (!chk(x,y)||!chk(x2,y2)||mp[x][y]!=mp[x2][y2]) {
x=rd()%n+1,y=rd()%m+1,d=rd()%4,x2=x+dir[d][0],y2=y+dir[d][1];
}
return dfs(x,y,x2,y2,1);
}
int main () {
freopen("game7.in","r",stdin);
freopen("game7.out","w",stdout);
srand(time(0));
sd=rand()+1;
scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
for (int i=1;i<=n;i++) {
for (int j=1;j<=m;j++) {scanf("%d",&mp[i][j]);}
}
while (!solve());
printf("1000 ");
for (int i=1;i<=500;i++) {printf("%d %d ",v1[500-i].first,v1[500-i].second);}
for (int i=1;i<=500;i++) {printf("%d %d ",v2[i-1].first,v2[i-1].second);}
return 0;
}
```
---
### 测试点 8:
$n=999,\ m=100,\ K=1,\ l_{min}=2,\ l_{max}=100000,\ c_1=0,\ c_2=1,\ F=0$,网格似乎很有规律。
这个点和 $6,7$ 不同的是我们需要找出的回文串非常长,不可能直接搜索,而是需要构造。
但是我们可以发现,网格几乎只由 $5,6$ 构成,并且如果 $i+j$ 是奇数那么 $(i,j)$ 上几乎都是 $6$;$i+j$ 是偶数那么 $(i,j)$ 上几乎都是 $5$,只有极少的反例(大概 $200$ 多个位置)。
我们称这些反例所在的位置是坏位置,其他位置是好位置。
那么如果一个长度为奇数的路径经过的都是好位置,则它是回文的,这点非常容易证明(它必是 $5,6$ 交替的一条路径),所以我们找到一个尽可能长的这种好路径即可。
我们可以两行两行构造,在相邻的两行中通过来回绕经过大部分格子,同时避开所有坏位置,如图中蓝色路径:
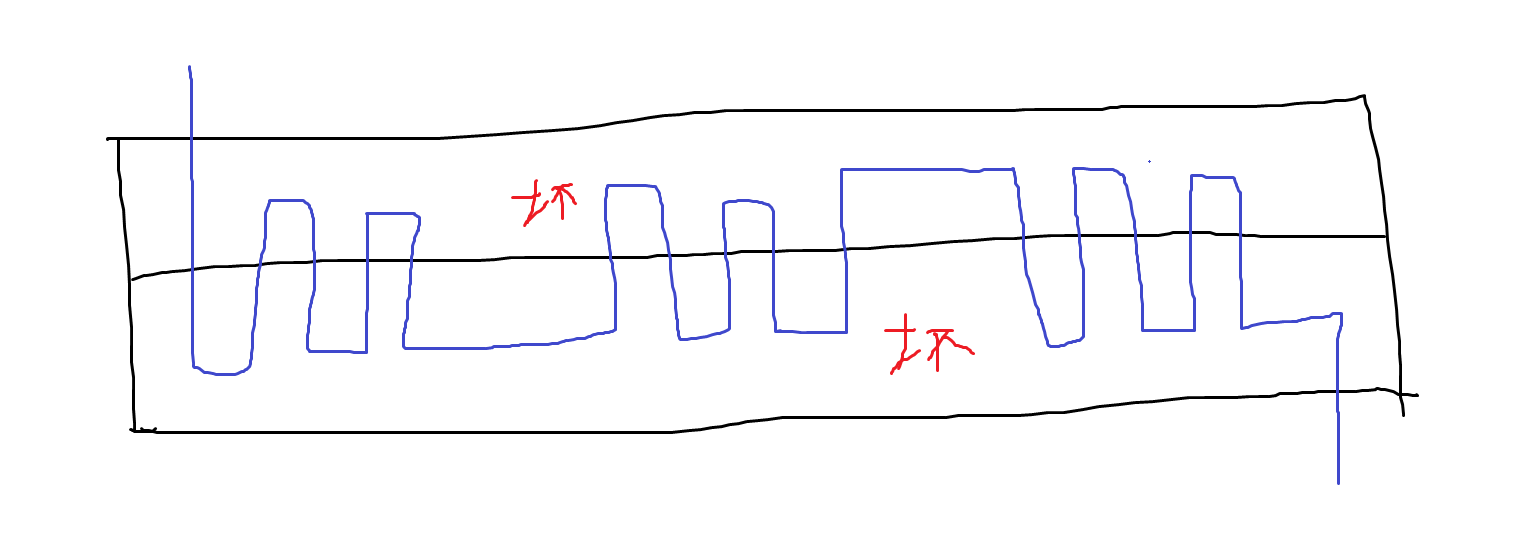
这做法看起来很好,但是有个 bug,就是如果两个坏位置把路给堵上了,就走不过去了。这时我们可以从旁边一行借个道,如图:
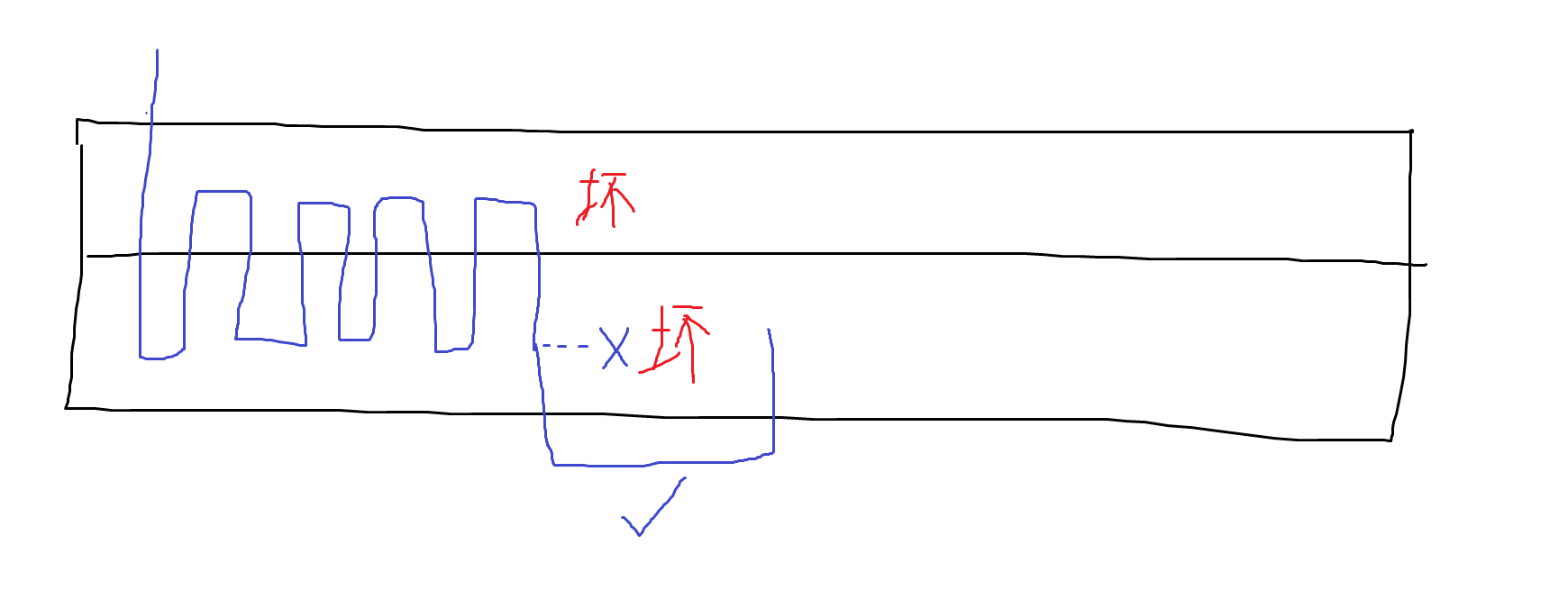
数据中只有 $3$ 个这样的情况,全都特判掉就行了(代码实现时因为一些原因,将行列互换了),最后构造出的长度是 $99475$。
```cpp
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=1010;
int n,m,k,l1,l2,c1,c2,f,mp[N][N],vis[N][N],dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
vector < pair<int,int> > v;
ull sd;
ull rd () {sd^=(sd<<27);sd^=(sd>>19);sd^=(sd<<25);return sd;}
bool chk (int x,int y) {return (x>0&&y>0&&x<=n&&y<=m&&mp[x][y]!=-1&&!vis[x][y]);}
void solve (int l,int x,int d) {
if (l==101) {return;}
//cerr << x << " " << l << endl;
assert(vis[x][l]==0);
v.push_back(make_pair(x,l));
vis[x][l]=1;
if (x==818&&l==19) {solve(l+1,x,d);return;}
if (x==818&&l==20) {
v.push_back(make_pair(818,21));vis[818][21]=1;
v.push_back(make_pair(817,21));vis[817][21]=1;
v.push_back(make_pair(816,21));vis[816][21]=1;
solve(l,x-2,d);return;
}
if (x==235&&l==76) {
v.push_back(make_pair(235,77));vis[235][77]=1;
v.push_back(make_pair(234,77));vis[234][77]=1;
v.push_back(make_pair(233,77));vis[233][77]=1;
solve(l,x-2,d);return;
}
if (x==269&&l==77) {solve(l+1,x,d);return;}
if (x==269&&l==78) {
v.push_back(make_pair(269,79));vis[269][79]=1;
v.push_back(make_pair(270,79));vis[270][79]=1;
v.push_back(make_pair(271,79));vis[271][79]=1;
solve(l,x+2,d);return;
}
if (d==0) {
if (x==n) {
if (l&1) {solve(l+1,x,0);}
else {solve(l+1,x,1);}
} else if (l&1) {
if (chk(x,l+1)&&chk(x+1,l+1)) {solve(l+1,x,d);}
else {solve(l,x+1,d);}
} else {
if (chk(x,l-1)&&chk(x+1,l-1)) {solve(l-1,x,d);}
else {solve(l,x+1,d);}
}
} else {
if (x==1) {
if (l&1) {solve(l+1,x,1);}
else {solve(l+1,x,0);}
} else if (l&1) {
if (chk(x,l+1)&&chk(x-1,l+1)) {solve(l+1,x,d);}
else {solve(l,x-1,d);}
} else {
if (chk(x,l-1)&&chk(x-1,l-1)) {solve(l-1,x,d);}
else {solve(l,x-1,d);}
}
}
}
int main () {
freopen("game8.in","r",stdin);
freopen("game8.out","w",stdout);
srand(time(0));
sd=rand()+1;
scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
for (int i=1;i<=n;i++) {
for (int j=1;j<=m;j++) {
scanf("%d",&mp[i][j]);
if ((i+j)&1) {
if (mp[i][j]!=6) {vis[i][j]=1;cout << i << " " << j << endl;}
} else {
if (mp[i][j]!=5) {vis[i][j]=1;cout << i << " " << j << endl;}
}
}
}
solve(1,1,0);
if (v.size()%2==0) {v.pop_back();}
printf("%d ",v.size());
for (auto x:v) {assert(x.second<=100);printf("%d %d ",x.first,x.second);}
return 0;
}
```
---
### 测试点 9:
$n=129,\ m=128,\ K=5,\ l_{min}=2,\ l_{max}=20000,\ c_1=0,\ c_2=2,\ F=0$,网格似乎很有规律。
虽然 $K=5$,但是由于分数是根据平方计算,所以我们还是希望一条路径搞定,这样路径最长,分数最大。
用比较好的编辑器打开输入数据后可以观察到每行都几乎是回文的,于是我们可以发现,整个网格几乎关于中轴线对称,只有 $18$ 对位置例外。
那么和测试点 8 就差不多了,我们只考虑左半边,只要绕开这些不对称的坏位置,然后再把左半边的路径翻折到右半边,就一定是一条回文的路径了。
这个测试点由于坏位置很少,所以甚至不需要测试点 8 那样的特判,直接两行两行绕就可以了,最后构造出的长度是 $16440$。
```cpp
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=1010;
int n,m,k,l1,l2,c1,c2,f,mp[N][N],vis[N][N],dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
vector < pair<int,int> > v;
ull sd;
ull rd () {sd^=(sd<<27);sd^=(sd>>19);sd^=(sd<<25);return sd;}
bool chk (int x,int y) {return (x>0&&y>0&&x<=n&&y<=m&&mp[x][y]!=-1&&!vis[x][y]);}
void solve (int l,int x,int d) {
if (l==65) {return;}
v.push_back(make_pair(x,l));
vis[x][l]=1;
if (d==0) {
if (x==n) {
if (l&1) {solve(l+1,x,0);}
else {solve(l+1,x,1);}
} else if (l&1) {
if (chk(x,l+1)&&chk(x+1,l+1)) {solve(l+1,x,d);}
else {solve(l,x+1,d);}
} else {
if (chk(x,l-1)&&chk(x+1,l-1)) {solve(l-1,x,d);}
else {solve(l,x+1,d);}
}
} else {
if (x==1) {
if (l&1) {solve(l+1,x,1);}
else {solve(l+1,x,0);}
} else if (l&1) {
if (chk(x,l+1)&&chk(x-1,l+1)) {solve(l+1,x,d);}
else {solve(l,x-1,d);}
} else {
if (chk(x,l-1)&&chk(x-1,l-1)) {solve(l-1,x,d);}
else {solve(l,x-1,d);}
}
}
}
int main () {
freopen("game9.in","r",stdin);
freopen("game9.out","w",stdout);
srand(time(0));
sd=rand()+1;
scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
for (int i=1;i<=n;i++) {
for (int j=1;j<=m;j++) {scanf("%d",&mp[i][j]);}
for (int j=1;j<=64;j++) {
if (mp[i][j]!=mp[i][129-j]) {vis[i][j]=1;printf("%d %d\n",i,j);}
}
}
cout << endl;
solve(1,1,0);
for (int i=1;i<=n;i++) {
for (int j=1;j<=64;j++) {
if (!vis[i][j]) {printf("%d %d\n",i,j);}
}
}
printf("%d ",2*v.size());
for (auto x:v) {assert(x.second<=100);printf("%d %d ",x.first,x.second);}
reverse(v.begin(),v.end());
for (auto x:v) {assert(x.second<=100);printf("%d %d ",x.first,129-x.second);}
return 0;
}
```
---
### 测试点 10:
$n=3,\ m=999,\ K=10,\ l_{min}=2,\ l_{max}=2997,\ c_1=0,\ c_2=2,\ F=0$,网格似乎很有规律。
和测试点 9 一样,我们还是希望一条路径搞定,这里 $l_{max}=2997=n\times m$,所以最好是一条路径覆盖所有数。
继续观察网格规律,首先可以发现的是如果将每行三个数三个数划分,将每行看成 $333$ 个三元组构成的序列,则这个序列是回文的。
进一步观察,我们可以输出每个三元组的第一个数,发现每一行关于第一个数都是有周期的。
也就是说,整个网格有如下周期:
```
1 2 1 2 3 2 3 4 3 4 5 4 5 6 5 4 5 4 3 4 3 2 3 2 1 2 1
4 3 2 5 4 3 6 5 4 7 6 5 8 7 6 7 6 5 6 5 4 5 4 3 4 3 2
5 4 3 6 5 4 7 6 5 8 7 6 9 8 7 8 7 6 7 6 5 6 5 4 5 4 3
```
观察每行每个三元组的第一个数,第一行是 `1 2 3 4 5 4 3 2 1`,第二行是 `4 5 6 7 8 7 6 5 4`,第三行是 `5 6 7 8 9 8 7 6 5`,有很强的对称性,于是我们尝试对于这个周期解决子问题。
通过尝试或者暴搜,我们发现有一组规律性很强的解,它的前 $9$ 项就是 `1 2 3 4 5 4 3 2 1`,你能找到吗?
没错!它就藏在第一个 $3\times 3$ 块中:
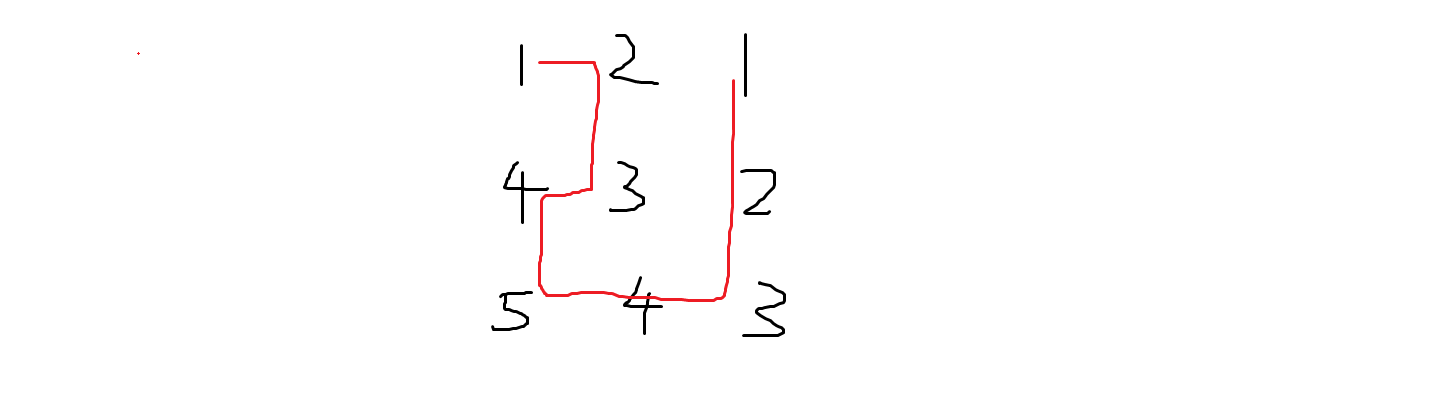
于是我们发现只要将每个 $3\times 3$ 块都像这样连起来,再把所有块串一起,就是一组合法的解。
```cpp
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=1010;
int n,m,k,l1,l2,c1,c2,f,mp[N][N];
int main () {
freopen("game10.in","r",stdin);
freopen("game10.out","w",stdout);
scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
for (int i=1;i<=n;i++) {
for (int j=1;j<=m;j++) {scanf("%d",&mp[i][j]);}
}
printf("2997\n");
for (int i=1;i<=333;i++) {
printf("%d %d %d %d %d %d %d %d ",1,i*3-2,1,i*3-1,2,i*3-1,2,i*3-2);
printf("%d %d %d %d %d %d %d %d %d %d ",3,i*3-2,3,i*3-1,3,i*3,2,i*3,1,i*3);
}
return 0;
}
```