「ICPC2017 WF」Money for Nothing
HenryHuang
·
·
题解
「ICPC2017 WF」Money for Nothing
我们可将生产商和消费商都看成二维平面上的点,其坐标分别为 (d_i,p_i),(e_i,q_i)。
那么问题转变为:
给定平面上的 m 个 A 类点 (d_i,p_i),以及 n 个 B 类点 (e_i,q_i)。求选择一个 A 类点作为矩形左下角,一个 B 类点作为矩形右上角所能得到的最大面积。若不存在这样的矩形就输出零。
考虑如下几种情况。
在这种情况下 A_1,A_2 都能与 B 围成一个矩形,但显然 A_1 更优秀。
故对于这样的 A 点我们可以直接舍弃。
在这种情况下 B_1,B_2 都能与 A 围成一个矩形,但显然 B_1 更优秀。
故对于这样的 B 点我们可以直接舍弃。
舍弃掉这些点过后两种点在平面上的排布一定是这样的:
然后我们考虑这样一种情况:
设 A_1,B_1 围成的矩形是以 A_1 为左下角的矩形当中最大的那一个。
我们可以得到这样一个结论:
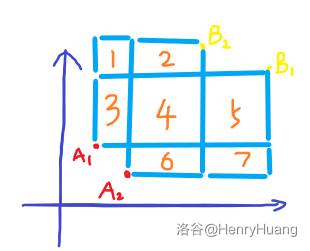
我们给这几个部分编个号,下面用编号代替上图中的部分。
根据我们前面的条件,有 $3+4+5>3+4+1+2\rightarrow 5>1+2$。
我们要证明的即 $4+6+5+7>4+6+2\rightarrow 5+7>2\rightarrow 1+2+7> 2$。
所以我们推广一下可以得到这样一个结论:对于每个红点,其围成最大矩形的黄点具有单调性。
根据这个性质我们直接分治就好了。
总时间复杂度为 $O(n\log_2n)$。
```cpp
/*---Author:HenryHuang---*/
/*---Never Settle---*/
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=5e5+5;
struct cc{
int x,y;
LL operator*(const cc &h)const{
return 1ll*(h.x-x)*(h.y-y);
}
}a[maxn],b[maxn],p[maxn];
int sa,sb;
LL Ans;
void solve(int l,int r,int ll,int rr){
if(l>r||ll>rr) return ;
int mid=(l+r)>>1;
LL ans=-1e18,id=0;
for(int i=ll;i<=rr;++i){
if(a[mid].x<b[i].x||a[mid].y<b[i].y){
if(a[mid]*b[i]>ans){
ans=a[mid]*b[i];
id=i;
}
}
}
if(id!=0){
solve(l,mid-1,ll,id);
solve(mid+1,r,id,rr);
Ans=max(Ans,ans);
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int m,n;cin>>m>>n;
for(int i=1;i<=m;++i){
cin>>p[i].x>>p[i].y;
}
sort(p+1,p+m+1,[&](cc a,cc b){return a.x==b.x?a.y<b.y:a.x<b.x;});
a[++sa]=p[1];
for(int i=2;i<=m;++i){
if(a[sa].y>p[i].y) a[++sa]=p[i];
}
for(int i=1;i<=n;++i){
cin>>p[i].x>>p[i].y;
}
sort(p+1,p+n+1,[&](cc a,cc b){return a.x==b.x?a.y<b.y:a.x<b.x;});
reverse(p+1,p+n+1);
b[++sb]=p[1];
for(int i=2;i<=n;++i){
if(b[sb].y<p[i].y) b[++sb]=p[i];
}
reverse(b+1,b+sb+1);
for(int i=1;i<=sb;++i) cout<<b[i].x<<' '<<b[i].y<<'\n';
solve(1,sa,1,sb);
cout<<Ans<<'\n';
return 0;
}
```