题解:P9614 [CERC2019] Ponk Warshall
hcx2012
·
·
题解
题意
给定两个字符串(字符集只含 A、C、G 或 T),求把第一个字符串通过交换两个字母变为第二个字符串的最少交换次数。
令前一个字符串为 s_1,后一个为 s_2。设值域 V=4。
注意本题解中,如果两个点 u,v 可以一步互达(即既有一条连接 u\rightarrow v 的边,又有一条连接 v\rightarrow u 的边),也认为它们组成一个长度为 2 的环。
思考
考虑暴力,固定 s_1,枚举统计,显然过不去。
由 P12542 这题,我们可以想到要维护一个不停交换的序列,最好的方式是把序列转移到图上。
枚举 i,在 s_{1,i} 与 s_{2,i} 之间连一条有向边。
题中样例 #1 如图所示。
样例 #1 的答案为 2,手跑可以得到多组解法,这里列举一种:(仅改动 s_1,每行给出交换的下标,下标交换后改动,下同)
1 5
2 4
大小为 2 的环
可以发现样例 1 出现了两个大小为 2 的环。对于每个环,它们需要 1 次交换进行归位。
### 大小为 3 的环
考虑以下样例:
```plain
ACT
TAC
```
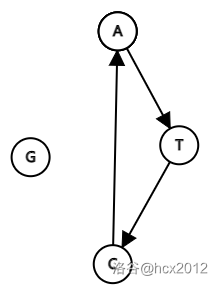
手跑发现这组数据的答案为 `2`,一组解为:
```plain
1 2
1 3
```
多枚举几组这样的数据可以发现:对于一个长度为 $3$ 的环需要 $2$ 次交换。
$O(V^3)$ 枚举三个点 $i,j,k$,它们之间应有 $i\rightarrow j$、$j\rightarrow k$、$k\rightarrow i$ 三条边,对于这样的环统计答案。
### 大小为 4 的环
考虑以下数据:
```plain
ACGT
CGTA
```
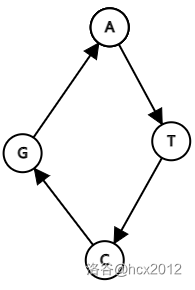
很容易发现这种数据的解为 `3`,一组可行解如下:
```plain
1 2
2 3
3 4
```
每个大小为 $4$ 的环需要 $3$ 次交换。这里的时间复杂度是 $O(V)$ 或 $O(V^4)$。
为什么会有两种?
因为前者运用一种取巧的方案,而后者直接枚举。
容易发现,此时处理余下部分就是大小为 $4$ 的环(因为一共只有 $V=4$ 个点),将剩下未处理的边数设为 $x$,则大小为 $4$ 的环共需要进行 $\frac{3}{4}x$ 次交换。
然后我们就用 $O(N+V^3)$ 的很低的复杂度完成了本题。
## 代码实现
```cpp
#include <bits/stdc++.h>
using namespace std;
int translate(char x){
if(x=='A')return 1;
if(x=='C')return 2;
if(x=='G')return 3;
if(x=='T')return 4;
}
int cnt[7][7];
int main(){
string s1,s2;
cin>>s1>>s2;
int n=s1.size();
s1=" "+s1;
s2=" "+s2;
for(int i=1;i<=n;i++){
cnt[translate(s1[i])][translate(s2[i])]++;
}
int ans=0;
// 2-cycles
for(int i=1;i<=4;i++){
for(int j=1;j<=4;j++){
if(i==j||cnt[i][j]>cnt[j][i])continue;
ans+=cnt[i][j];
cnt[j][i]-=cnt[i][j];
cnt[i][j]=0;
}
}
// 3-cycles
for(int i=1;i<=4;i++){
for(int j=1;j<=4;j++){
for(int k=1;k<=4;k++){
// i->j->k
if(i==j||i==k||j==k)continue;
int mn=min(min(cnt[i][j],cnt[j][k]),cnt[k][i]);
cnt[i][j]-=mn;
cnt[j][k]-=mn;
cnt[k][i]-=mn;
ans+=mn*2;
}
}
}
// 4-cycles
int res=0;
for(int i=1;i<=4;i++){
for(int j=1;j<=4;j++){
if(i==j)continue;
res+=cnt[i][j];
}
}
ans+=res*3/4;
cout<<ans;
return 0;
}
```