题解 P8141 【ICPC2020 WF】 What’s Our Vector, Victor?
warzone
·
·
题解
题目大意
你在一个 d 维空间中。
给出空间中 n 个点的坐标 \vec{y}_1,\vec{y}_2,\cdots,\vec{y}_n 及它们与你的距离 r_1,r_2,\cdots,r_n,
请你求出你所在的坐标 \vec{x}。
若有多个解,输出任意一个。
## 题解
给出一个 naive 的数形结合的做法。
根据题意,不难列出方程
$$
\begin{cases}
(\vec{x}-\vec{y}_1)^2=r_1^2\\
(\vec{x}-\vec{y}_2)^2=r_2^2\\
\cdots \\
(\vec{x}-\vec{y}_n)^2=r_n^2
\end{cases}
$$
这个方程含有平方,所以没法直接高斯消元。
但注意到
$$(\vec{x}-\vec{y})^2=\vec{x}^2-2\vec{y}\cdot\vec{x}+\vec{y}^2$$
其中 $\vec{x}^2$ 是相同的。
考虑将原点平移到 $\vec{y}_1$,设 $\vec{x}'=\vec{x}-\vec{y}_1,\forall k,\vec{y}_k'=\vec{y}_k-\vec{y}_1$,则
$$
\begin{cases}
\vec{x}'^2=r_1^2&(1)\\
(\vec{x}'-\vec{y}_2')^2=r_2^2\\
(\vec{x}'-\vec{y}_3')^2=r_3^2\\
\cdots\\
(\vec{x}'-\vec{y}_n')^2=r_n^2
\end{cases}
$$
下面 $n-1$ 个式子同时减去 $(1)$,得到
$$
\begin{cases}
-2\vec{y}'_2\cdot\vec{x}+\vec{y}_2'^2=r_2^2-r_1^2\\
-2\vec{y}'_3\cdot\vec{x}+\vec{y}_3'^2=r_3^2-r_1^2\\
\cdots\\
-2\vec{y}'_n\cdot\vec{x}+\vec{y}_n^2=r_n^2-r_1^2
\end{cases}
$$
这等价于线性方程组
$$A\vec{x}=\vec{a}$$
$$A=\begin{bmatrix}
(\vec{y}_2')^T\\
\hline(\vec{y}_3')^{T^{^{^{}}}}\\
\hline\vdots \\
\hline(\vec{y}_n')^{T^{^{^{}}}}
\end{bmatrix},\vec{a}=-\dfrac{1}{2}\begin{bmatrix}
r_2^2-r_1^2-\vec{y}_2^2\\
r_3^2-r_1^2-\vec{y}_3^2\\
\vdots\\
r_n^2-r_1^2-\vec{y}_n^2
\end{bmatrix}$$
高斯消元求解该线性方程组,若其有唯一解,则解就是答案。
---------------------
如果解不是唯一的怎么办?这时“形”便派上用场。
让我们转换一下题意:给定 $d$ 维空间中 $n$ 个超球,
球心为 $\vec{y}_1,\vec{y}_2,\cdots,\vec{y}_n$,半径为 $r_1,r_2,\cdots,r_n$,求它们的交点。
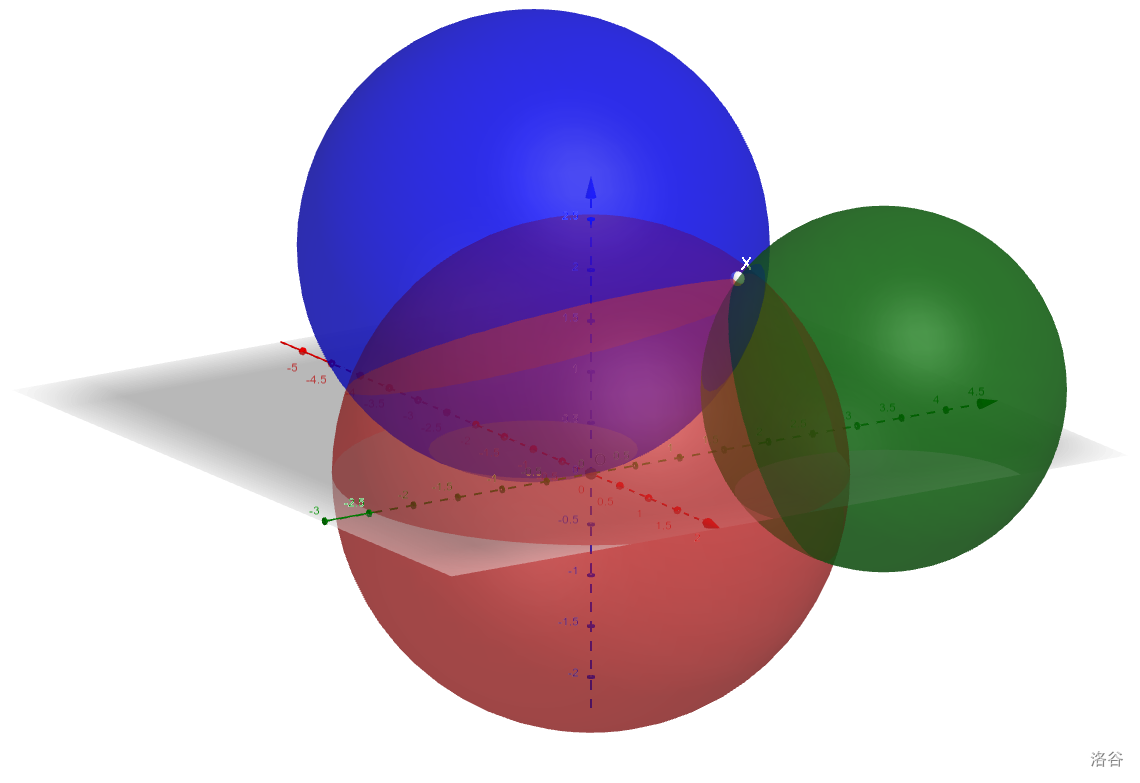
先把这个问题搁置一边,来看看这个高中文化课常用的 trick:
给定二维空间两个圆的方程:
$$
\begin{cases}
(x-a_1)^2+(y-b_1)^2=r_1^2&(1)'\\
(x-a_2)^2+(y-b_2)^2=r_2^2&(2)'
\end{cases}
$$
它们的交线如图所示:
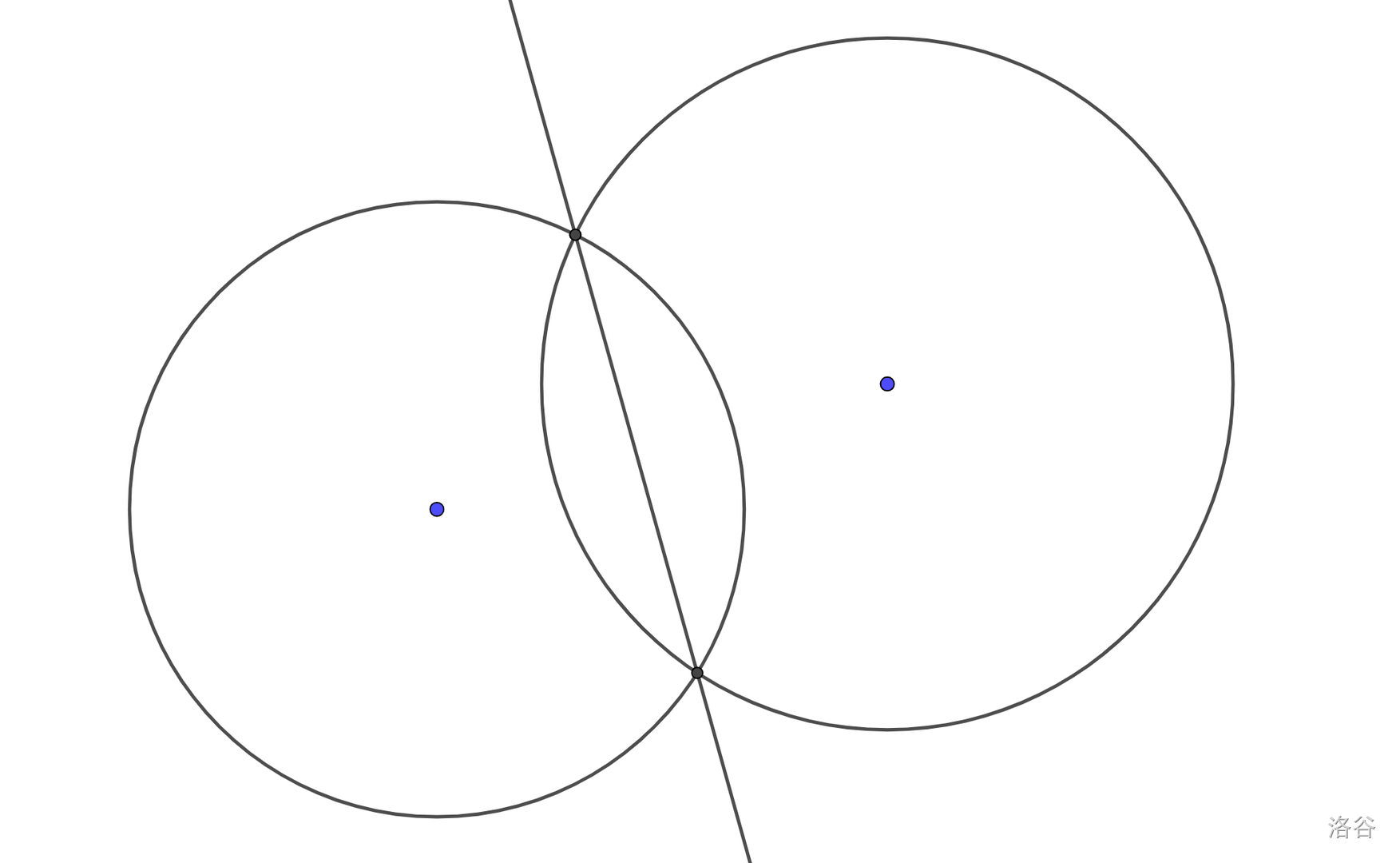
现在我们要求交线的方程,一般人的想法是将 $(1)',(2)'$ 联立,求得交点后再求交线。
但最快的方法是将 $(1)',(2)'$ 相减,直接求得交线的方程
$$(x-a_1)^2-(x-a_2)^2+(y-b_1)^2-(y-b_2)^2=r_1^2-r_2^2$$
接下来我们简短证明下这么做的正确性:
> - $(1)',(2)'$ 中 $x^2,y^2$ 系数均为 $1$,因此 $(1)'-(2)'$ 一定是个二元一次不定方程,
也就一定是一条直线。
> - $(2)'+[(1)'-(2)']=(1)'$,因此圆 $2$ 与该直线的交点一定在圆 $1$ 上。
同理,圆 $1$ 与该直线的交点一定在圆 $2$ 上。
因此该直线与两个圆中一个的交点等价于两个圆的交点。
> 综上,$(1)'-(2)'$ 就是两个圆的交线方程。
显然这个结论及其证明可以推广到高维空间,若已知三维空间两个球的方程:
$$
\begin{cases}
(x-a_1)^2+(y-b_1)^2+(z-c_1)^2=r_1^2&(1)''\\
(x-a_2)^2+(y-b_2)^2+(z-c_2)^2=r_2^2&(2)''\\
\end{cases}
$$
它们的交面如图所示:
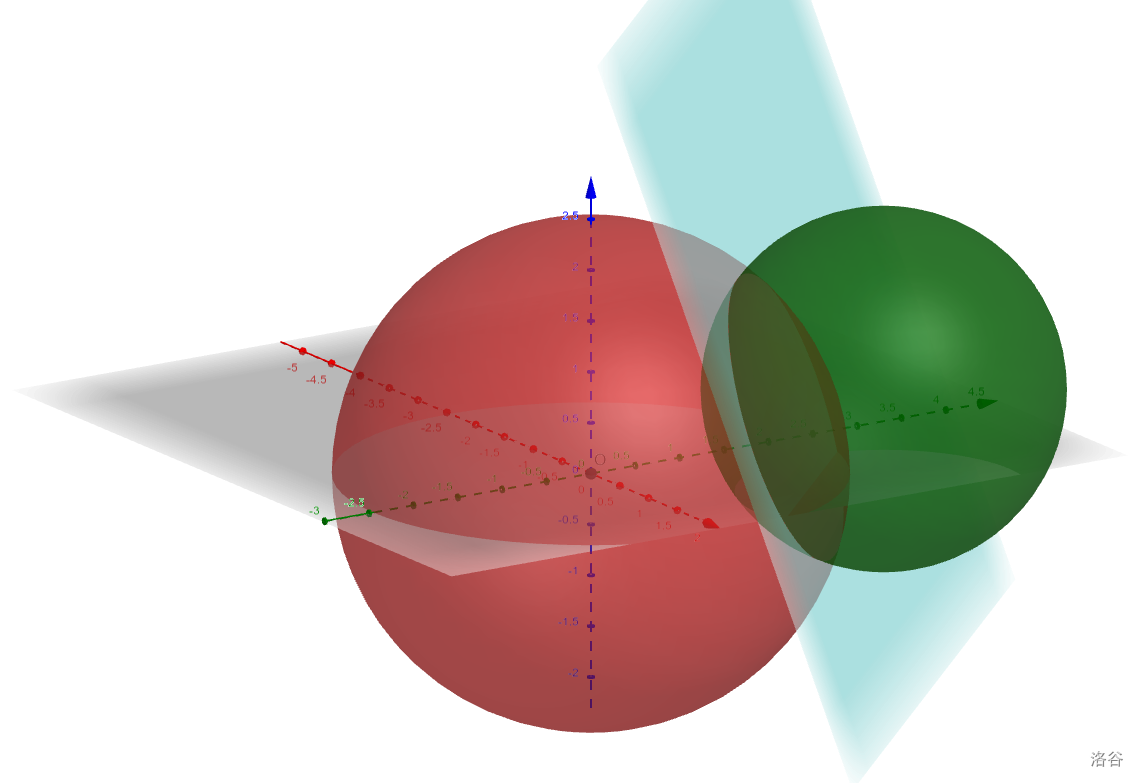
把 $(1)''$ 和 $(2)''$ 相减,可直接得到交面的方程
$$(x-a_1)^2-(x-a_2)^2+(y-b_1)^2-(y-b_2)^2+(z-c_1)^2+(z-c_2)^2=r_1^2-r_2^2$$
且交面与其中一个球的交点等价于两球的交点。
同理,若已知 $d$ 维空间的两个超球:
$$
\begin{cases}
(\vec{x}-\vec{y}_1)^2=r_1^2\\
(\vec{x}-\vec{y}_2)^2=r_2^2
\end{cases}
$$
将两个超球的方程相减,可得到 $d-1$ 维超交面的方程
$$(\vec{x}-\vec{y}_1)^2-(\vec{x}-\vec{y}_2)^2=r_1^2-r_2^2$$
且超交面与其中一个超球的交点等价于两个超球的交点。
此时我们已经能解释之前的高斯消元在做什么了:
- 将所有方程减去 $(1)$ 等价于求超球 $1$ 与其他所有超球的超交面方程。
- 高斯消元等价于求这些超交面的交。
- 这些超交面的交与超球 $1$ 的交点都是合法的解,即所有超球的交点。
---------------------------------
分析完这些后,解不唯一的情况变成了一个这样的问题:
设高斯消元后自由元的个数为 $k$,
则我们需要求解一个 $d$ 维超球和一个 $k$ 维 “平面” (准确的说是线性流形)的交点。
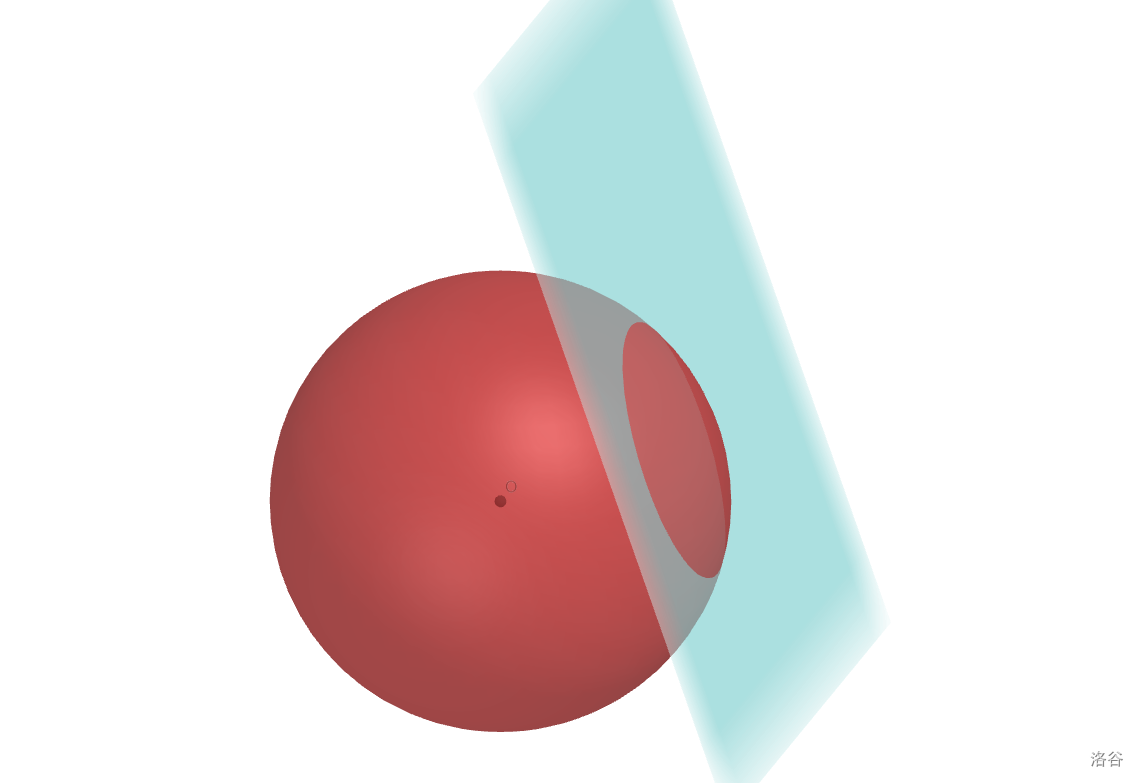
同样考虑二维空间的情况:求解一个圆和一条直线的交点。
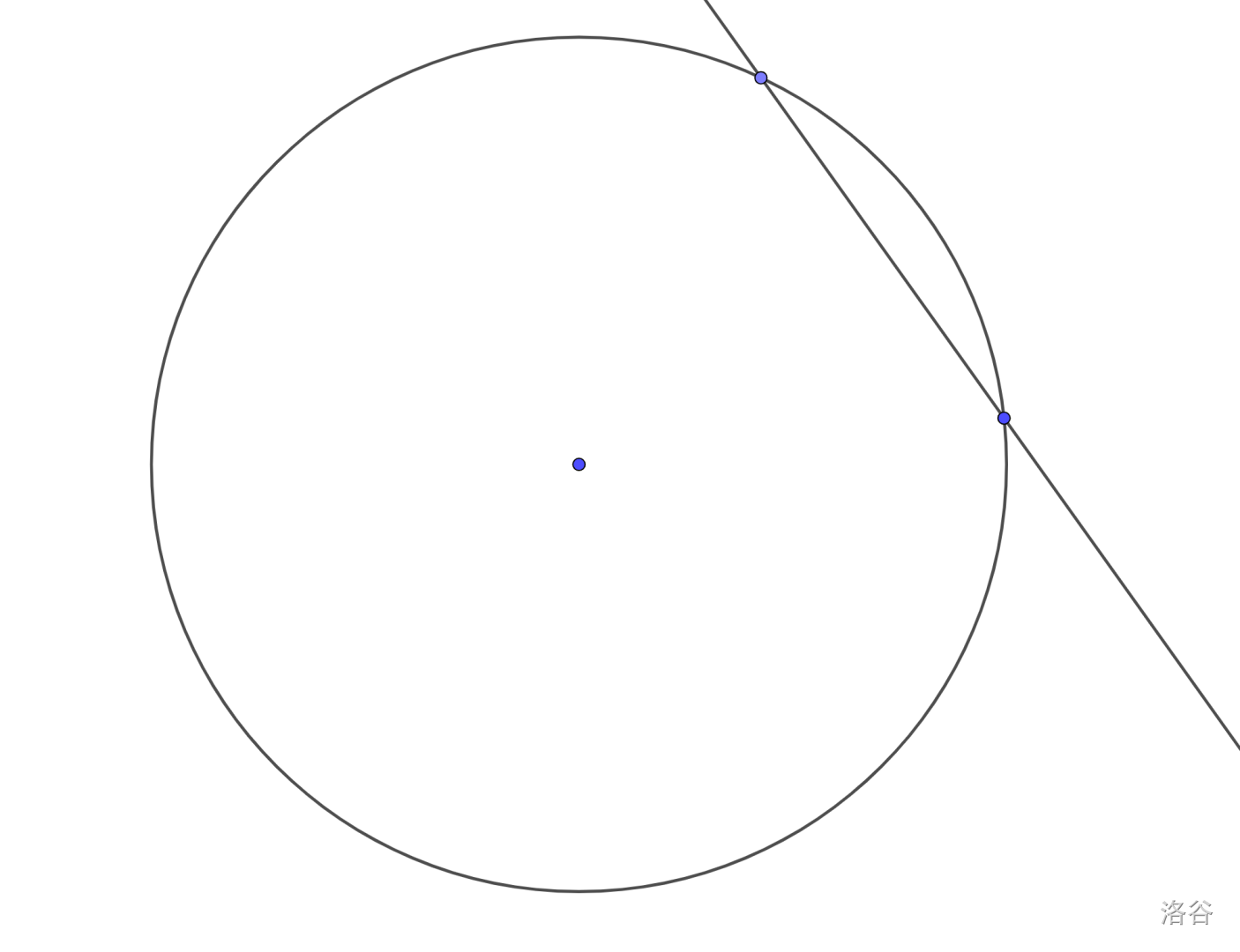
一个显然的做法是过圆心向直线作垂线,然后勾股定理算出垂足到交点的距离:
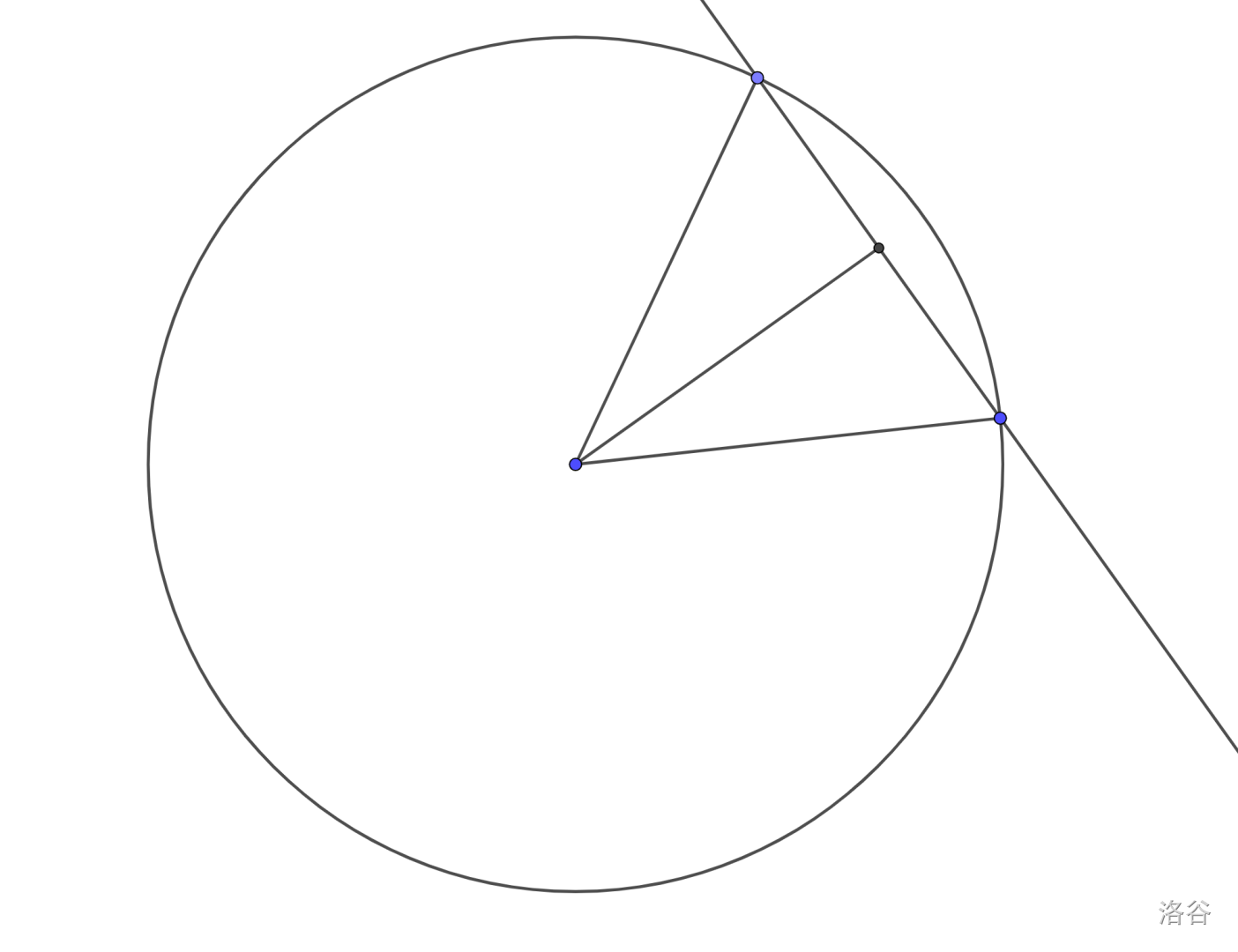
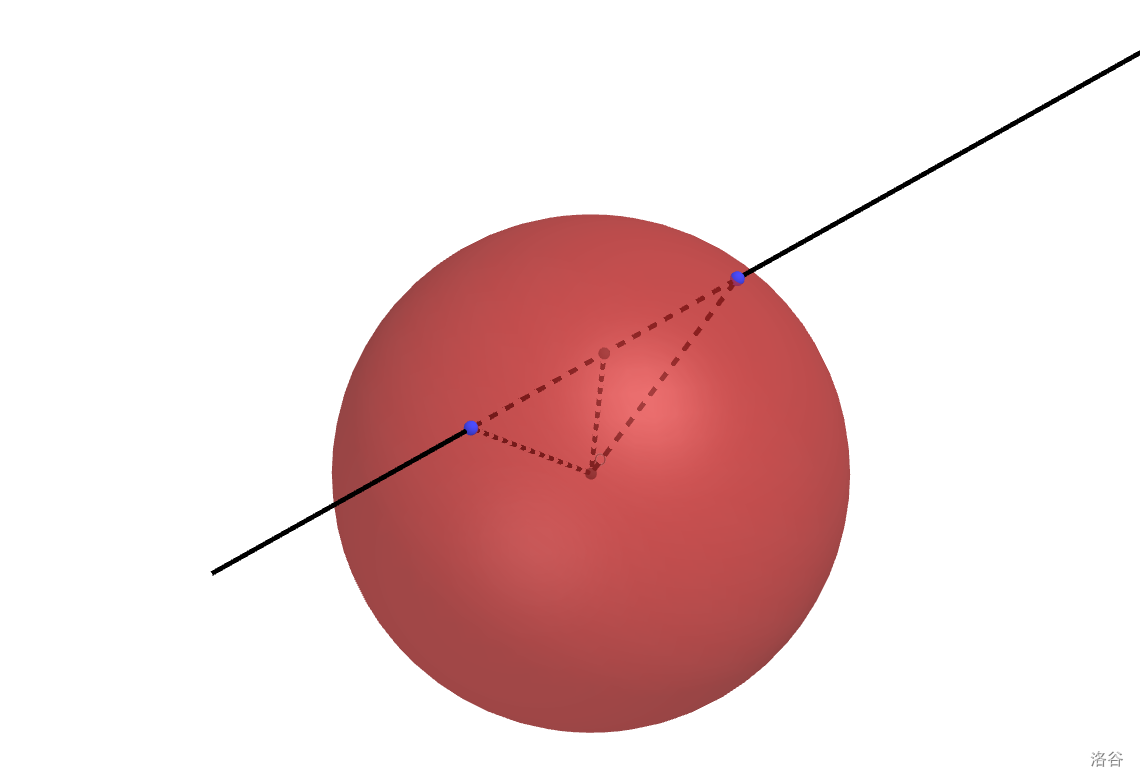
拓展到三维空间时,情况是类似的:
- 对于三维空间一条直线和球相交,跟刚才的情况是一样的。
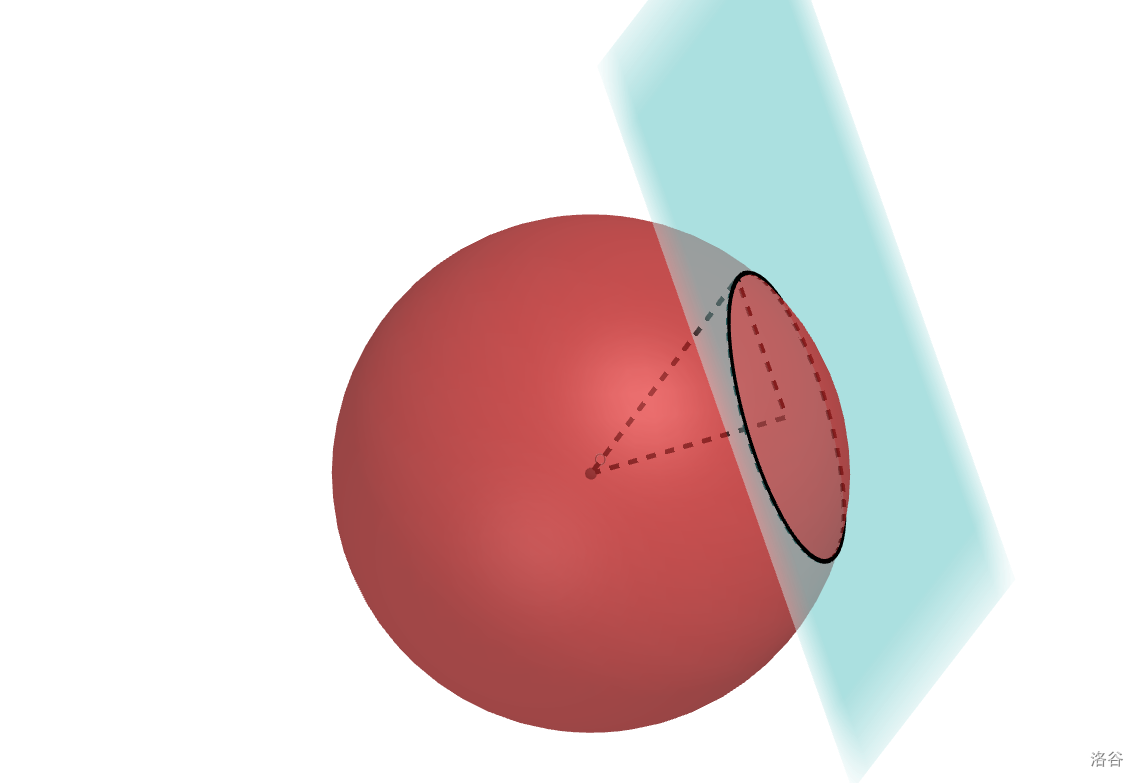
- 对于三维空间一个平面和球相交,可以确定截面一定是个圆。
同样作垂线得到圆心后勾股定理求解。
想一想怎么归纳到高维空间,提示一下:一维空间的超球是两个点。
$\qquad
\qquad
答案揭晓:d 维空间一个超球与一个 k(k\le d) 维线性流形相交,截面一定是个 k 维超球。
过原超球球心向线性流形作垂线即可得到截面的球心,再勾股定理即可得到球心的半径。
我们由此得到求解原问题的一个大致的思路:
- 过超球心向线性流形作垂线,求出垂足的坐标 \vec{p}。
- 勾股定理算出截面的半径 r'。
- 在线性流形上随便找一个长度为 r' 的向量 \vec{q},\vec{p}+\vec{q} 就是一个合法的解。
回到之前的线性方程组。高斯消元后,其一定会变为如下形式:
\left[
\begin{array}{ccccc|}
1&&&&&v_{1,1}&v_{2,1}&\cdots&v_{k,1}\\
&1&&&&v_{1,2}&v_{2,2}&\cdots&v_{k,2}\\
&&\ddots&&&\vdots&\vdots&\vdots&\vdots\\
&&&1&&v_{1,d-k-1}&v_{2,d-k-1}&\cdots&v_{k,d-k-1}\\
&&&&1&v_{1,d-k}&v_{2,d-k}&\cdots&v_{k,d-k}\\
\hline 0&0&0&0&0&0&0&0&0\\
\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots
\end{array}\right]
\begin{bmatrix}
x_1\\x_2\\\vdots\\x_{d-k}\\\hline x_{d-k+1}\\ x_{d-k+2}\\ \vdots \\x_d
\end{bmatrix}=\begin{bmatrix}
a_1'\\ a_2'\\ \vdots\\ a_{d-k}'\\\hline 0\\0\\ \vdots \\0
\end{bmatrix}
简记为如下形式:
\left[\begin{array}{c|c|c|c|c}
I&\vec{v}_1&\vec{v}_2&\cdots&\vec{v}_k\\
\hline O&\vec{0}&\vec{0}&\vec{0}&\vec{0}
\end{array}\right]
\begin{bmatrix}\vec{x}_0\\ \hline\vec{x}_1\end{bmatrix}
=\begin{bmatrix}\vec{a}'\\ \hline\vec{0}\end{bmatrix}
我们需要确定线性方程组的解集,从而确定整个线性流形。
- 若 \vec{x}_1=\vec{0},显然 \vec{x}_0=\vec{a}'。
因此 \begin{bmatrix}\vec{a}'\\ \hline\vec{0}\end{bmatrix} 是该线性方程组的一组特解。
- 若 x_{d-k+1}=\lambda,x_{d-k+2}=x_{d-k+3}=\cdots=x_d=0,
则 \vec{x}_0+\lambda\vec{v}_1=\vec{a}',\vec{x}_0=\vec{a}-\lambda\vec{v}_1。
因此 x_{d-k+1} 每增加 \lambda,\vec{x}_0 就要减去 \lambda\vec{v}_1。
综上,设
\vec{u}_1=\begin{bmatrix}-\vec{v}_1\\\hline 1\\0\\0\\0\\ \vdots\end{bmatrix}
,\vec{u}_2=\begin{bmatrix}-\vec{v}_2\\\hline 0\\1\\0\\0\\ \vdots\end{bmatrix},
\vec{u}_3=\begin{bmatrix}-\vec{v}_3\\\hline 0\\0\\1\\0\\ \vdots\end{bmatrix},\cdots
\vec{b}=\begin{bmatrix}
\vec{a}'\\ \hline \vec{0}
\end{bmatrix},V=\{[\vec{u}_1|\vec{u}_2|\cdots|\vec{u}_k]\vec{x}_1|\vec{x}_1\in\mathbb{R}_k\}
则线性方程组的解集为
X=\{\vec{b}+\vec{\Delta}|\vec{\Delta}\in V\}
即线性空间 V 内的所有向量加上特解 \vec{b},与线性流形的定义一致。
接下来考虑作垂线,由于球心为 \vec{0},V 的基底为 \vec{u}_1,\vec{u}_2,\cdots,\vec{u}_k,
我们的目标是找出 \vec{p}\in X,使得 \vec{p} 与 V 中所有的基向量垂直,即
\vec{u}_1\cdot \vec{p}=\vec{u}_2\cdot\vec{p}=\cdots=\vec{u}_k\cdot \vec{p}=0
\qquad{(2)}
把 \vec{p} 拆开:
\vec{p}=\vec{b}+[\vec{u}_1|\vec{u}_2|\cdots|\vec{u}_k]\vec{x}_1\qquad{(3)}
然后将 (2) 表示成矩阵形式:
\begin{bmatrix}
\vec{u}_1^T\\
\hline\vec{u}_2^{T^{^{^{}}}}\\
\hline\cdots\\
\hline\vec{u}_k^{T^{^{^{}}}}
\end{bmatrix}(\vec{b}+[\vec{u}_1|\vec{u}_2|\cdots|\vec{u}_k]\vec{x}_1)=\vec{0}
注意到 \begin{bmatrix}\vec{u}_1^T\\\hline\vec{u}_2^{T^{^{^{}}}}\\\hline\cdots\\\hline\vec{u}_k^{T^{^{^{}}}}
\end{bmatrix}[\vec{u}_1|\vec{u}_2|\cdots|\vec{u}_k] 为 k 阶方阵 ,因此高斯消元解线性方程组
\begin{bmatrix}\vec{u}_1^T\\\hline\vec{u}_2^{T^{^{^{}}}}\\\hline\cdots\\\hline\vec{u}_k^{T^{^{^{}}}}
\end{bmatrix}[\vec{u}_1|\vec{u}_2|\cdots|\vec{u}_k]\vec{x}_1=-\begin{bmatrix}\vec{u}_1^T\\\hline\vec{u}_2^{T^{^{^{}}}}\\\hline\cdots\\\hline\vec{u}_k^{T^{^{^{}}}}
\end{bmatrix}\vec{b}
即可得到 \vec{x}_1,代入 (3) 即可求出 \vec{p}。
因为过线性流形(直线/平面)上一点有且只有一条直线与该流形(直线/平面)垂直,
这个线性方程组一定有唯一解,也就一定能解出 \vec{p}。
解出 \vec{p} 后,勾股定理得到
r'=\sqrt{r^2-\vec{p}^2}
然后 \vec{p}+\dfrac{r'}{\sqrt{\vec{u}_1^2}}\vec{u}_1 就是一组合法的解了。
最后不要忘记,我们一开始将原点平移到了 \vec{y}_1,要平移回去才行哦!
Code
/*
this code is made by warzone
2022.3.11 15:30
*/
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
typedef double db;
struct READ{//快读
char c,w;
inline READ(){c=getchar();}
template<typename type>
inline READ& operator >>(type& num){
for(w=1;'0'>c||c>'9';c=getchar())
w=c=='-'? -1:1;
for(num=0;'0'<=c&&c<='9';c=getchar())
num=num*10+(c-'0');
if(c=='.') for(db i=1;c=getchar(),'0'<=c&&c<='9';)
i*=0.1L,num+=i*(c-'0');
return num*=w,*this;
}
}cin;
int d,n;
int pos[512],pos_[512];
db y[512],r;
db A[512][512],a[512];
db B[512][512],b[512];
int top,top_;
template<typename type1,typename type2,typename type3>
inline void gauss(type1 &A,type2 &a,type3 &pos,//高斯消元
int &top,const int d,const int n){
top=d;
for(int id=0;id<top&&id<n;++id){
while(A[id][id]==0){
for(int i=id+1;i<n;++i) if(A[i][id]){
for(int j=id;j<d;++j)
std::swap(A[id][j],A[i][j]);
std::swap(a[id],a[i]);break;
}
if(A[id][id]==0){//把消元失败的维度放到最后面
if(id>=--top) return;
std::swap(pos[top],pos[id]);
for(int i=0;i<n;++i)
std::swap(A[i][id],A[i][top]);
}
}
if(A[id][id]!=1){
db get=A[id][id];
for(int i=id+1;i<d;++i) A[id][i]/=get;
A[id][id]=1,a[id]/=get;
}
for(int i=0;i<n;++i) if(i!=id&&A[i][id]){
db get=A[i][id];
for(int j=id+1;j<d;++j) A[i][j]-=A[id][j]*get;
A[i][id]=0,a[i]-=a[id]*get;
}
}
}
inline void print(){//平移回来并输出答案
for(int i=0;i<d;++i) y[pos[i]]+=a[i];
for(int i=0;i<d;++i) printf("%0.6lf ",y[i]);
}
int main(){
cin>>d>>n;
for(int i=0;i<d;++i) cin>>y[i],pos[i]=i;//输入 (1) 式
cin>>r,--n;
for(int id=0;id<n;++id){
for(int i=0;i<d;++i){//减去 (1) 式
cin>>A[id][i],A[id][i]-=y[i];
a[id]+=A[id][i]*A[id][i];
}
db get;
cin>>get,a[id]=(a[id]+r*r-get*get)/2;
}
gauss(A,a,pos,top,d,n),top=std::min(top,n);//第一次高斯消元
if(top==d) return print(),0;//唯一解
for(int i=top;i<d;++i) A[i][i]=-1;
const int k=d-top;
for(int id=0;id<k;++id){//计算 \vec{p} 的线性方程组
pos_[id]=id;
for(int i=0;i<k;++i)
for(int j=0;j<d;++j)
B[id][i]+=A[j][id+top]*A[j][i+top];
for(int j=0;j<d;++j)
b[id]-=A[j][id+top]*a[j];
}
gauss(B,b,pos_,top_,k,k);//第二次高斯消元
for(int id=0;id<k;++id)//将 \vec{x}_1 代回 \vec{p}
for(int i=0;i<d;++i)
a[i]+=b[id]*A[i][id+top];
db r_=r*r,r__=0;
for(int i=0;i<d;++i){//勾股定理计算 r'
r__+=A[i][top]*A[i][top];
r_-=a[i]*a[i];
}
r_=sqrtl(r_/r__);
for(int i=0;i<d;++i) a[i]+=A[i][top]*r_;
return print(),0;
}