Torch 题解
0000pnc
·
2024-10-15 23:29:33
·
题解
题意简述:有两个人 Alice 和 Bob,两人各有一个火炬。Alice 初始在数轴上的 0 号点,Bob 初始在 1 号点。两人都会以 1 单位/秒的速度往右移动,但是只能在各自的火炬燃烧的时候移动。
Alice 的火炬可以持续燃烧 a_2 秒,之后需要 b_2 秒重新点燃,而 Bob 的火炬可以燃烧 a_1 秒,熄灭后需要 b_1 秒重新点燃。由于 Bob 比较胖所以 Alice 永远不能与 Bob 走到同一个点(即:如果 Bob 站在 Alice 前面一格不动,则 Alice 的火炬即使在燃烧也不能移动)。开始的时候两人的火炬均为刚刚点燃的状态,而在过程中如果某人的火炬熄灭则他会立刻开始点燃。有 n 次询问,每次询问给出 q_i ,问开始 q_i 秒后 Alice 的位置。
部分分:对于 $20\%$ 的数据有 $q_{i} \le 10^6$。
对于另 $20\%$ 的数据有 $a_1=a_2$,$b_1=b_2$。
### 算法 1
注意到前两个点的 $q_{i}\le 10^{6}$,所以直接把询问排个序然后模拟就可以。时间复杂度 $\mathcal{O}(\max q_{i})$,期望得分 $20$ 分。
### 算法 2
当 $a_{1}=a_{2}$,$b_{1}=b_{2}$ 时 Alice 和 Bob 的行动方式是完全一致的,都是走 $a_{1}$ 秒然后停 $b_{1}$ 秒,找到周期后可以 $\mathcal{O}(1)$ 算出之前走了多少步,期望得分 $20$ 分。
~~合并上述两个算法可以得到 $40$ 分,此时可以放弃了,要不然就会像我一样冲这题然后挂成 $50$。~~
### 算法 3
考虑这个过程的本质是什么。把 Bob 的移动写成 0/B 序列 $s$,即 $a_{1}$ 个 $B$ 和 $b_{1}$ 个 $0$ 不断循环。那么 $s_{x}=B$ 就说明 Bob 在 $x$ 时刻移动,否则停在原地。
接着,同上把 Alice 的移动序列也写成 0/A 序列 $t$。
考虑先尝试把所有的 $B$ 和 $A$ 进行匹配,且每个 $B$ 只能匹配它右边(或者同位置上)的最近的还没有匹配的 $A$。以 $a_{1}=1$,$b_{1}=2$,$a_{2}=4$,$b_{2}=5$ 为例:
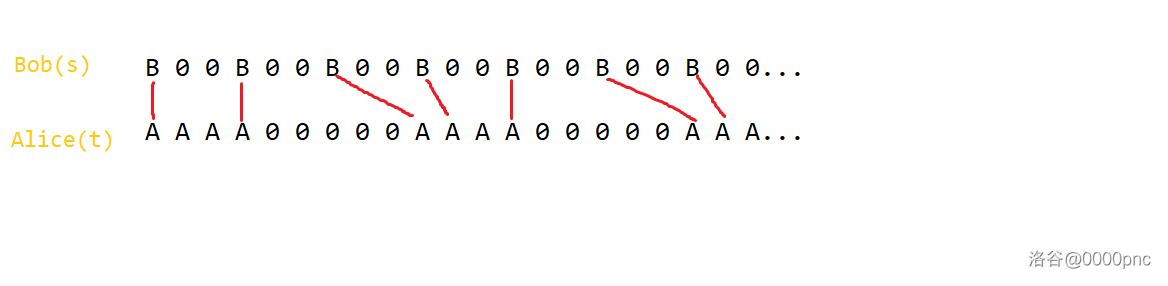
*图一:示例*
经过简单观察后发现,Alice 可以在 $x$ 时刻移动,当且仅当 $t_{x}=A$ 且这个 $A$ 能匹配上某个 $B$。
证明也比较容易:考虑归纳,现在在考虑位置 $x$,那么可以假设前面的位置均满足该性质。
对于必要性,如果 $t_{x}=0$ 那么显然 Alice 不能在 $x$ 时刻移动。如果 $t_{x}$ 没有匹配上,则说明 $x$ 前面有若干个 $A$ 已经与前面的所有 $B$ 匹配上了(如图中的第 2,3 个 A 就属于这种情况)。这时设 Bob 走了 $k$ 步,那 Alice 也一定走了 $k$ 步,这是因为前面已经匹配了 $k$ 个 $A$,根据归纳假设 Alice 在那些匹配的位置都移动了。所以此时 Alice 应该正好贴在 Bob 后面。而此时 $s_{x}$ 必然为 $0$(否则 $s_{x}$ 可以与 $t_{x}$ 匹配,矛盾),所以 Bob 在本轮不会移动,因此 Alice 也不能移动。
充分性比较显然,如果 $t_{x}=A$ 且这个 $A$ 能匹配上,那么假设在 $x$ 位置及前面 Bob 走了 $k$ 步(即 $x$ 及前面有 $k$ 个 $B$),那么根据归纳假设 Alice 在 $x$ 之前最多走过 $k-1$ 步,因为 $x$ 是第 $k$ 个被匹配的位置。所以这次移动是合法的,即 Alice 确实可以在 $x$ 位置移动一步。
因此可以将原题面转化成这个问题:
> 给定 $a_{1},b_{1},a_{2},b_{2}$,构造无限长的序列 $s$ 为 $a_{1}$ 个 $B$ 和 $b_{1}$ 个 $0$ 循环交替出现,序列 $t$ 为 $a_{2}$ 个 $A$ 和 $b_{2}$ 个 $0$ 循环交替出现。现在对于序列 $s$ 中的每个 $s_{x}=B$,将其匹配到距离其最近的还没匹配过的 $t_{y}=A$ 上(并且需要满足 $y \ge x$)。多次询问,每次给定 $q$,询问有多少个 $t_{x}=A(x \le q)$ 能被匹配上。
下面来解决这个问题。
$s$ 和 $t$ 都是有周期的。因此可以取一个 $s$ 和 $t$ 的公共周期(设其长度为 $p$)来进行考虑。
考虑直接对第一个周期进行暴力模拟。$p$ 可以达到 $10^{12}$ 的级别,所以显然不能一秒一秒的推。注意到 $A$ 的连续段和 $B$ 的连续段不会很多(都是 $10^{6}$ 量级),可以将所有还没有匹配的 $A$ 和 $B$ 表示成若干段区间,然后用这些区间来加速匹配。具体的,每次取出一个最左边的 $s$ 的区间 $[L,R]$,然后找到最左边的右端点 $\ge L$ 的 $t$ 的区间 $[l,r]$ 进行匹配即可。细节见图:
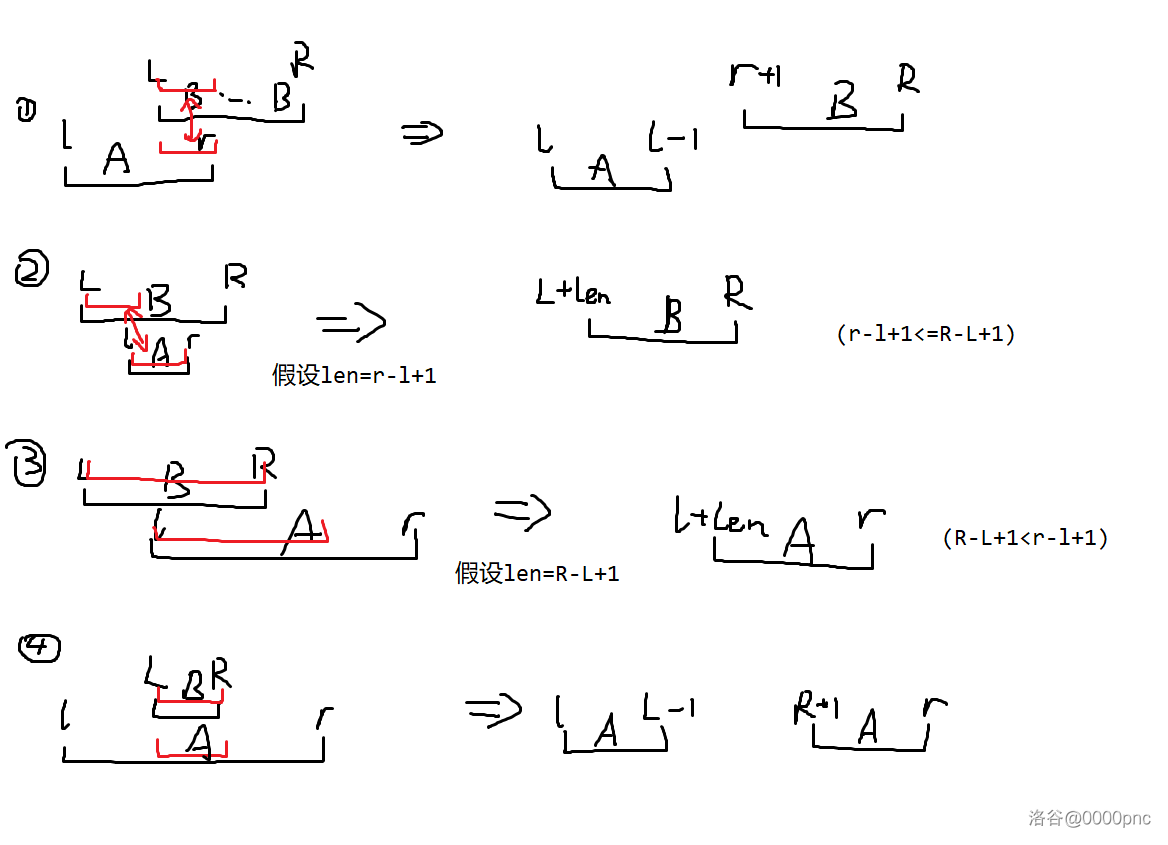
*图二:红笔是需要匹配(即删除)的区间*
如果用 `set` 维护区间删除和分裂,这部分的时间复杂度就是 $\mathcal{O}(a\log a)$(默认全部的输入参数同阶)。
做完第一个周期之后,可能会剩下一些没有匹配的 $A$ 和 $B$。设没有匹配的 $B$ 有 $k_{1}$ 个,没有匹配的 $A$ 有 $k_{2}$ 个(比如图一中周期长度是 $9$,就有 $2$ 个 $A$ 和 $1$ 个 $B$ 没有在第一周期找到匹配)。
接下来是一个关键观察:对于第二个及以后的周期,在匹配完这个周期的全部 $A$ 和 $B$ 之后,会有 $\max(0,k_{2}-k_{1})$ 个 $A$ 尚未匹配,而没有匹配的 $B$(这些都会匹配到后面周期的 $A$)的数量依然是 $k_{1}$。
**Proof:**
归纳。设在考虑第 $i$ 个周期,前 $i-1$ 个周期均满足条件。
先不考虑前面周期对于第 $i$ 个周期的影响,直接做一遍正常的匹配。做完之后结果和第一个周期是一样的,会剩下 $k_{2}$ 个 $A$ 和 $k_{1}$ 个 $B$ 还没有匹配。
接下来,前面还剩下一些未匹配的 $B$,需要考虑这些 $B$ 对结果带来的影响。
如果前面的周期剩下的 $B$ 的个数已经超过了 $k_{1}$,那么说明前面的所有 $A$ 都已被匹配,即这个周期也不会剩下任何 $A$。显然这种情况对应的是 $k_{2}\lt k_{1}$。(这部分可能需要感性理解)
否则,前面的周期只会留下 $k_{1}$ 个尚未匹配的 $B$,且一定是上一个周期留下来的。
由于此时必有 $k_{2} \ge k_{1}$,所以前面留下来的 $k_{1}$ 个 $B$ 都必须与这个周期的 $k_{2}$ 个 $A$ 匹配。不过直接匹配是不满足要求的,但是可以进行一些调整使得它满足要求(见图)。
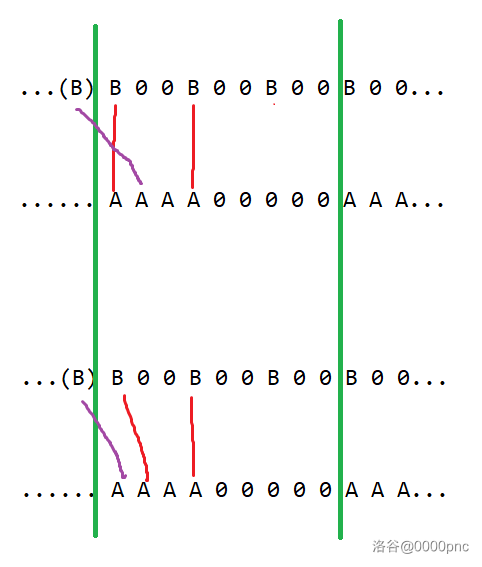
*图三:如图,上面直接将前面剩下的 B 与这里没有匹配的 A 匹配是不合法的,不过可以通过不断调整两个交叉的匹配使其合法(下图)。*
因此,留下来的 $k_{1}$ 个 $B$ 能在不影响其他地方的情况下与 $k_{2}$ 个 $A$ 中的前 $k_{1}$ 个进行“匹配”。随后这个周期也会剩下来 $k_{1}$ 个 $B$ 没有匹配。因此完成了证明。
这个性质表明,这个匹配是有周期性的,除了第一个周期外,其余的周期都有确定位置的 $\max(0, k_{2}-k_{1})$ 个 $A$ 没有匹配。因此对于每一个询问 $q$,可以求出其所在周期 $i$,第 $1$ 到 $i-1$ 周期的贡献是易求的,而对于 $i$ 周期只需求出在这个周期的 $\max(0, k_{2}-k_{1})$ 个没有匹配的 $A$ 中有多少个在 $q$ 前面即可。由于之前使用了 `set` 维护没有匹配的区间,此时可以直接 `set` 里二分求出这个东西。这部分时间复杂度为 $\mathcal{O}(n\log a)$。当然你也可以把询问离线排序后扫一遍来替代每次询问时的二分,复杂度 $\mathcal{O}(n\log n)$。(推荐离线,常数较小)
空间复杂度分析:瓶颈在于用 `set` 进行模拟,同一时间内最多有 $\mathcal{O}(a)$ 个区间,因此空间复杂度为 $\mathcal{O}(a)$。
于是我们用 $\mathcal{O}(n\log n+a\log a)$ 的时间复杂度,$\mathcal{O}(a)$ 的空间复杂度解决了该问题,可以获得 100 分。
具体实现的细节可能较多。
----
upd 2025.5.24: 发现这是原题,交个题解先,但是这个做法感觉有点幽默了。
代码:
```cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL T, n, LCM, a[3], b[3], ans[1000005];
pair<LL, LL> pos[2000005];
set<pair<LL, LL> > intv, opr, ok;
LL k, pre[4000005];
map<LL, LL> rnk;
struct qry {
int id; LL q;
} e[1000005];
bool cmp(qry x, qry y) { return (x.q + LCM - 1) % LCM < (y.q + LCM - 1) % LCM; }
LL read() {
LL x = 0; char ch = getchar();
while (ch < '0' || ch > '9') ch = getchar();
while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
return x;
}
void write(LL x, char ed) {
if (x >= 10) write(x / 10, 0);
putchar(x % 10 + '0');
if (ed) putchar(ed);
}
vector<pair<LL, LL> > split(pair<LL, LL> res, pair<LL, LL> oc) {
vector<pair<LL, LL> > ret;
if (res.first < oc.first) ret.push_back({res.first, oc.first - 1});
if (res.second > oc.second) ret.push_back({oc.second + 1, res.second});
return ret;
}
void work() {
a[1] = read(), b[1] = read(), a[2] = read(), b[2] = read(), n = read();
swap(a[1], a[2]), swap(b[1], b[2]);
int g = __gcd(a[1] + b[1], a[2] + b[2]), sm1 = (a[1] + b[1]) / g, sm2 = (a[2] + b[2]) / g;
LCM = 1ll * (a[1] + b[1]) * (a[2] + b[2]) / g;
for (int i = 1; i <= sm2; i++) intv.insert({1ll * (a[1] + b[1]) * (i - 1) + 1, 1ll * (a[1] + b[1]) * (i - 1) + a[1]});
for (int i = 1; i <= sm1; i++) opr.insert({1ll * (a[2] + b[2]) * (i - 1) + 1, 1ll * (a[2] + b[2]) * (i - 1) + a[2]});
while (1) {
if (opr.empty() || intv.empty()) break;
auto p = *(opr.begin());
while (1) {
while (!intv.empty() && (*intv.begin()).second < p.first) ok.insert(*intv.begin()), intv.erase(intv.begin());
if (intv.empty()) break;
auto it = intv.begin();
auto q = *it; intv.erase(it);
LL st = max(p.first, q.first), len = min(q.second - st + 1, p.second - p.first + 1);
if (q.second - q.first + 1 != len) {
auto vec = split(q, {max(p.first, q.first), max(p.first, q.first) + len - 1});
for (auto Q : vec) intv.insert(Q);
}
if (p.second - p.first + 1 != len) {
auto P = split(p, {p.first, p.first + len - 1})[0];
opr.erase(p), opr.insert(P); p = P;
}
else { opr.erase(p); break; }
}
}
while (!intv.empty()) ok.insert(*intv.begin()), intv.erase(intv.begin());
ok.insert({LCM + 1, LCM});
int tt = 0;
for (auto p : ok) {
rnk[p.first] = ++tt; pos[tt] = p;
pre[tt] = pre[tt - 1] + p.second - p.first + 1;
}
LL cnt = 0;
for (auto p : opr) cnt += p.second - p.first + 1;
LL all = pre[tt], all2 = max(0ll, pre[tt] - cnt);
for (int _ = 1; _ <= n; _++) e[_].q = read(), e[_].id = _;
sort(e + 1, e + n + 1, cmp);
int cur = 0;
for (int _ = 1; _ <= n; _++) {
LL tx = (e[_].q - 1) % LCM + 1, blc = (e[_].q + LCM - 1) / LCM, al = (blc - 1) * a[1] * sm2 + tx / (a[1] + b[1]) * a[1] + min(1ll * a[1], tx % (a[1] + b[1]));
while (cur < tt && pos[cur].first < tx) cur++;
if (tt == 1) { ans[e[_].id] = al; continue; }
pair<LL, LL> p = pos[cur];
LL ct = 0;
if (cur == 1) {
if (p.first == tx) ct++;
}
else {
if (p.first == tx) ct++;
else {
p = pos[cur - 1];
ct = min(tx - p.first + 1, p.second - p.first + 1);
}
}
if (e[_].id == 1) cerr << ct << endl;
LL res = 1ll * max(0ll, blc - 2) * all2 + all * (blc != 1), pr = pre[rnk[p.first] - 1];
ans[e[_].id] = al - res - (blc == 1 ? pr + ct : max(0ll, pr + ct - cnt));
}
for (int i = 1; i <= n; i++) write(ans[i], '\n');
set<pair<LL, LL> >().swap(intv), set<pair<LL, LL> >().swap(ok), set<pair<LL, LL> >().swap(opr);
map<LL, LL>().swap(rnk);
return ;
}
int main() {
T = read();
while (T--) work();
return 0;
}
```