CF802E题解
luuia
·
·
题解
题目传送门
前置知识:泊松分布和均匀分布
泊松分布
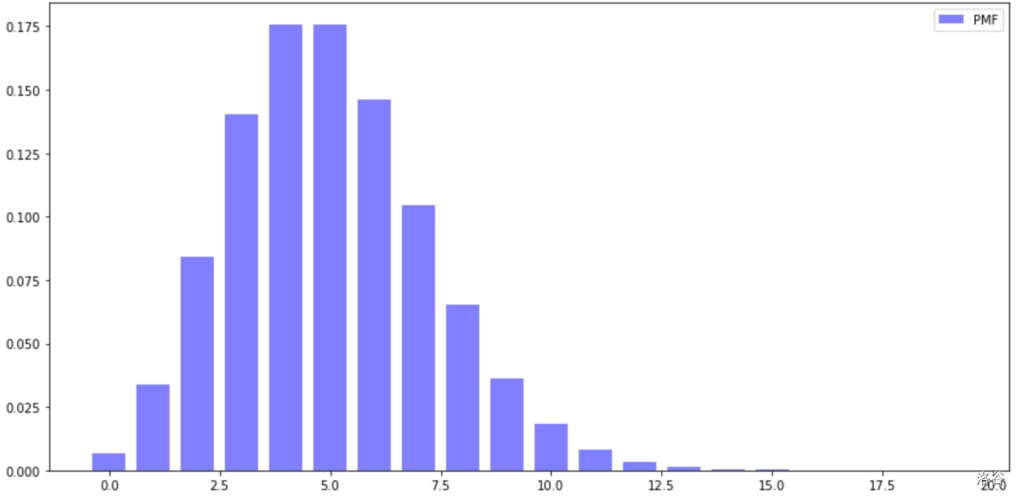
我们看到,这张图里大部分数据集中于中间的几段,而分布较远的则几乎趋近于 $0$。像这种类似于正态分布的分布图象,被称为 $\text{Poisson}$ 分布。
下面是几个 $\text{Poisson}$ 分布的性质:
- 泊松分布的概率函数为:
$$P(x = k) = {{\lambda ^ k} \over {k!}}e^{-\lambda},k = 0,1,\cdots$$
- 特征函数为:
$$\psi(t) = exp(\lambda(e ^{it} - 1))$$
$1.$ 泊松分布是一种描述和分析稀有事件的概率分布。要观察到这类事件,样本含量必须很大。
$2.$ $\lambda$ 是泊松分布所依赖的唯一参数。$\lambda$ 值愈小,分布愈偏倚,随着增大,分布趋于对称。
$3.$当 $\lambda = 20$ 时分布泊松分布接近于正态分布;当 $\lambda = 50$ 时,可以认为泊松分布呈正态分布。实际上,当 $\lambda \geq 20$ 时就可以用正态分布来近似地处理泊松分布的问题。
### 均匀分布
在概率论和统计学中,均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。
记数据中最小值为 $a$,最大值为 $b$,则概率函数可以如下表示:
$$f(x)= \begin{cases} \frac{1}{b - a} & a < x < b \\ 0 & else.\end{cases}$$
**那么,如何用 $\text{OI}$ 实现判断两者呢?**
## 分析
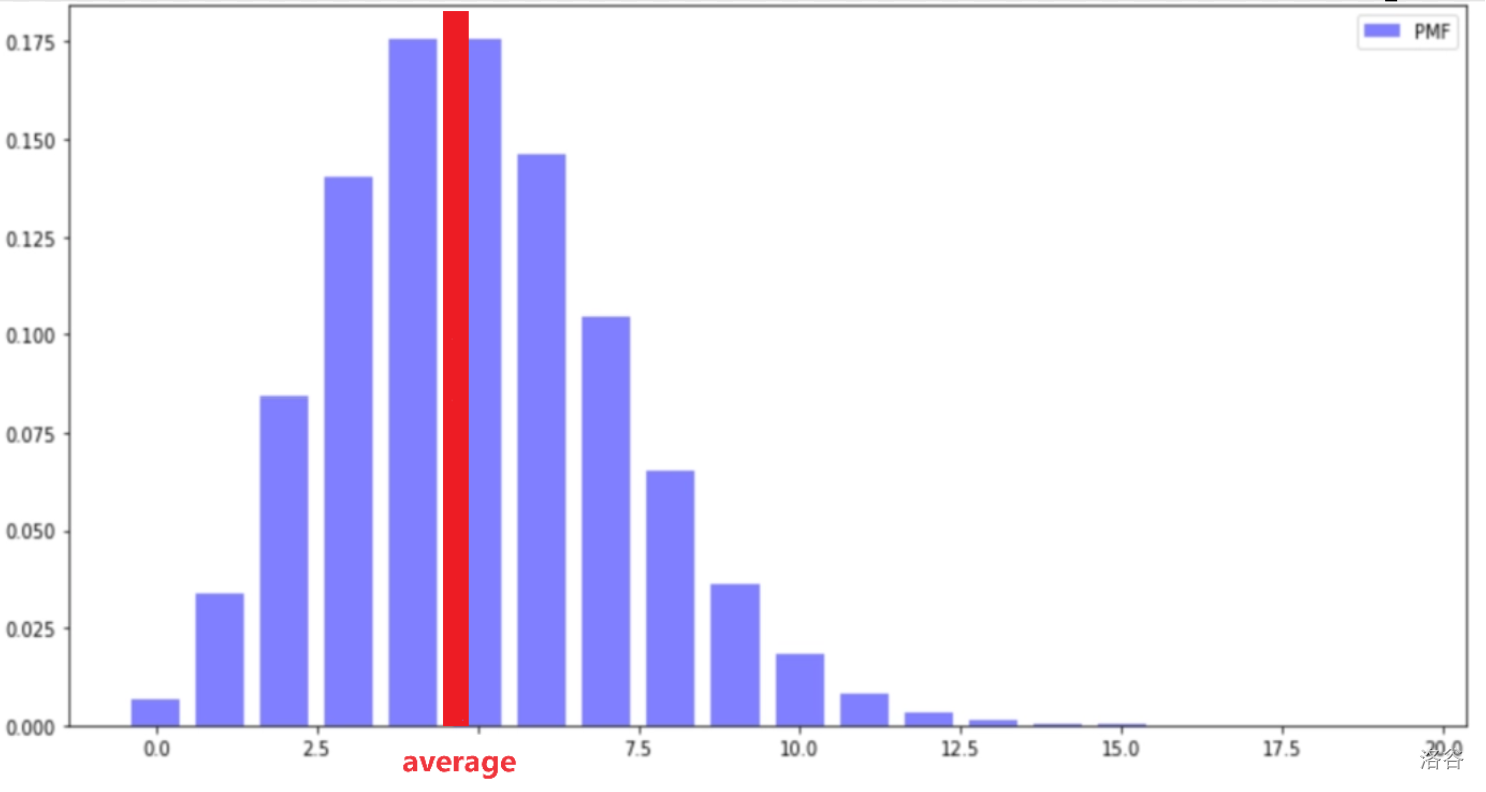
我们看到,泊松分布主要是集中在中部,那么我们求出整个数列的平均值,如果 $80 \%$ 的数据都分布在平均值的两侧不远,我们就判定这组数据为泊松分布,否则为均匀分布。
如果为泊松分布,那么输出整个数列的平均数 $\text{average}$,如果为均匀分布,由上面所讲的概率函数,输出最大值和最小值的平均数即可。
## 代码
下面是 AC 代码 $\,\,\,$ [AC 记录](https://www.luogu.com.cn/record/141735115)
```cpp
#include<bits/stdc++.h>
using namespace std;
int a[255],ans,sum,minn,maxn;
int work()
{
minn = 2e9,maxn = -1;
sum = 0;
ans = 0;
for(int i = 1;i <= 250;i++)
{
cin >> a[i];
sum += a[i];//计算数据的和,从而计算平均数
minn = min(minn,a[i]);//最小值
maxn = max(maxn,a[i]);//最大值
}
double average = (double)sum / 250;
double averaged = average / 2;//应当大致分布于平均值的两侧且与平均值的差在平均值的一半以内
for(int i = 1;i <= 250;i++)
{
if(a[i] - average < averaged && a[i] - average > 0 - averaged) ans++;//统计符合的个数
}
if(ans >= 200) return (int)average;//大于 80%即 200个
else return (int)maxn * 0.5 - minn * 0.5;
}
int main()
{
int T;
cin >> T;
while(T--)
{
cout << work() << endl;
}
return 0;
}
```