[THUPC2021] 小 E 爱消除
Time_tears
·
·
题解
看完题目后容易想到区间 Dp。
设 g_{l,r} 表示区间 [l,r] 的答案(包含最少的剩的和最小栈大小两个信息),最后 g_{1,n} 就是答案。
g 的转移
我们假设第一步先选最左边(右边同理)。
situation 1.
直接把最左边然后不管它,转移式为:
g_{l,r}=g_{l+1,r}+(1,1)
situation 2.
考虑让最左边的值去和中间的某一个相同值抵消,枚举 i(c_i=c_l),现在我们要让 c_i,c_l 抵消
situation 2.1
那么我们设 $f_{l_1,r_1,l_2,r_2}$ 表示将 $[l_1,r_1,l_2,r_2]$ **完全删除**至少需要多大的栈,此时的 $g_{l,r}$ 可以由 $g_{j+1,i-1}$ 和 $f_{l+1,j,i+1,r}$ 转移得到,画成示意图大概是这个样子:
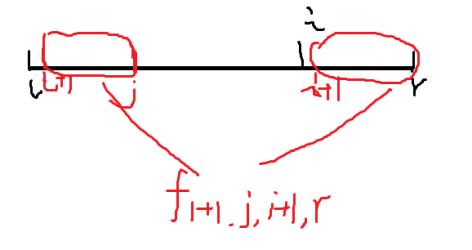
#### situation 2.2
$[l+1,i-1]$ 必须要仙贝选到栈中且要被完全删除,但是我们也有可能再用右边的一段来帮助它消除,假设用了 $[j,r](j>i)$ 来帮助它删除。
那么此时 $g_{l,r}$ 可以由 $g_{i+1,j-1}$ 和 $f_{l+1,i-1,j,r}$ 转移得到。
## $f$ 的转移
同理,考虑枚举从哪边开始删,枚举相同的数的位置然后枚举辅助删除的 $j$ 的位置转移即可,理解了上面的转移下面是一模一样的。
这个算法的复杂度是 $O(n^6)$ 的,但是因为 $f$ 的转移中,$r_2-l_2+r_1-l_1\bmod 2=0$ 否则无解这个限制,常数大约可以缩减 $\dfrac{1}{4}$ 左右,同时 $[l_1,r_1,l_2,r_2]$ 这个区间必须要将区间中的数两两配对才有可能消除,这个地方也可以使常数大大减小,只要用一个 Hash 或者你预处理一下就行了,真正的复杂度为 $O(可过)$,~~压行代码~~。
```cpp
#include<bits/stdc++.h>
#define pr pair<int,int>
#define mp make_pair
#define fi first
#define se second
using namespace std;
const int inf=0x3f3f3f3f;
int n,c[55],h[55],s[55];
int f[55][55][55][55];
pr g[55][55];
pr operator+(pr a,pr b){return mp(a.fi+b.fi,a.se+b.se);}
int F(int l1,int r1,int l2,int r2) {
if(l1>r1&&l2>r2)return 0;
if((r1-l1+r2-l2&1)||(s[l1-1]^s[r1]^s[l2-1]^s[r2]))return inf;
if(l1>r1)l1=1,r1=0;if(l2>r2)l2=1,r2=0;
int &ans=f[l1][r1][l2][r2];if(ans)return ans;ans=inf;
for(int i=l1; i<=r1; ++i) {
if(i!=l1&&c[i]==c[l1])for(int j=l2-1; j<=r2; ++j)ans=min(ans,max(max(F(l1+1,i-1,j+1,r2)+1,2),F(i+1,r1,l2,j)));
if(l2<=r2&&c[i]==c[r2])for(int j=l2-1; j<r2; ++j)ans=min(ans,max(max(F(l1,i-1,j+1,r2-1)+1,2),F(i+1,r1,l2,j)));
}
for(int i=l2; i<=r2; ++i) {
if(i!=r2&&c[i]==c[r2])for(int j=r1+1; j>=l1; --j)ans=min(ans,max(max(F(l1,j-1,i+1,r2-1)+1,2),F(j,r1,l2,i-1)));
if(l1<=r1&&c[i]==c[l1])for(int j=r1+1; j>l1; --j)ans=min(ans,max(max(F(l1+1,j-1,i+1,r2)+1,2),F(j,r1,l2,i-1)));
} return ans;
}
pr G(int l,int r) {
if(g[l][r].se)return g[l][r];
if(l>r)return mp(0,0);
pr &ans=g[l][r];ans=mp(inf,inf);
ans=min(ans,min(G(l+1,r)+mp(1,1),G(l,r-1)+mp(1,1)));
for(int i=l; i<=r; ++i) {
if(i!=l&&c[i]==c[l]) {
for(int j=l+1,tmp; j<=r; ++j)
if((tmp=F(l+1,min(i,j)-1,max(i,j)+1,r))<inf) {
pr wer=(i>=j)?G(j,i-1):G(i+1,j);
ans=min(ans,mp(wer.fi,max(wer.se,max(2,tmp+1))));
}
}
if(i!=r&&c[i]==c[r]) {
for(int j=l,tmp; j<=r-1; ++j)
if((tmp=F(l,min(i,j)-1,max(i,j)+1,r-1))<inf) {
pr wer=(i>=j)?G(j,i-1):G(i+1,j);
ans=min(ans,mp(wer.fi,max(wer.se,max(2,tmp+1))));
}
}
}
return ans;
}
int main() {
cin>>n,srand((unsigned)time(NULL));
for(int i=1; i<=n; ++i)cin>>c[i],h[i]=rand();
for(int i=1; i<=n; ++i)s[i]=s[i-1]^h[c[i]];
cout<<G(1,n).fi<<" "<<G(1,n).se<<"\n";
return 0;
}
```