题解 AGC046F 【Forbidden Tournament】
jun头吉吉
·
·
题解
题意
定义 H 有四个点 a,b,c,d 构成,并且满足 a\to\ b,\ b\to\ c,\ c\to\ a,\ a\to\ d,\ b\to\ d,\ c\to\ d 。
问有 N 个点且每个点度数不超过 K 的竞赛图的数目使得不存在 H。
## 题解
这 都 能 数 ?
以下内容 $a\to b$ 表示有从 $a$ 到 $b$ 的有向边。$a\to b$ 和 $b\not\to a$ 是等价的。
以下内容需要用到的结论有如果竞赛图有环,那么一定存在三元环。~~证明留作习题~~ 就考虑一个 $>3$ 的环中间割一条边变成一个较小的环,最终肯定可以到达三元环。
题目中禁止出现的子图,直观的理解就是**三元环上三个点都连向一个点**。
很厉害的题目。考虑如果有入度为 $0$ 的点,那么可以把这个点删掉变成一个 $N-1,K-1$ 的子问题。所以我们枚举删了 $i$ 个点,就是一个 $N-i,K-i$ 的子问题,系数是 $\binom Nii!$,删除这 $i$ 个点是有顺序的。
然后接下来我们考虑的问题**每个点至少有一个入度**。
考虑我们拉出来一个点 $v$,记 $Y=\{w|v\to w\}$,也就是 $v$ 的出边连向的点的集合,$X=V\setminus Y$,也就是 $v$ 的入边加上 $v$ 自己。
然后如果 $X$ 中有环,也就是有三元环,首先 $v$ 肯定不在环内,那么这个环都向 $v$ 连边,然后就构成了 $H$。所以我们得到了第一条结论:
**结论$\mathrm I.$** $X$ 是一个 DAG,存在一个 $x_1,\dots,x_k$ 且 $x_k=v$ ,满足若 $i<j$,则 $x_i\to x_j$。
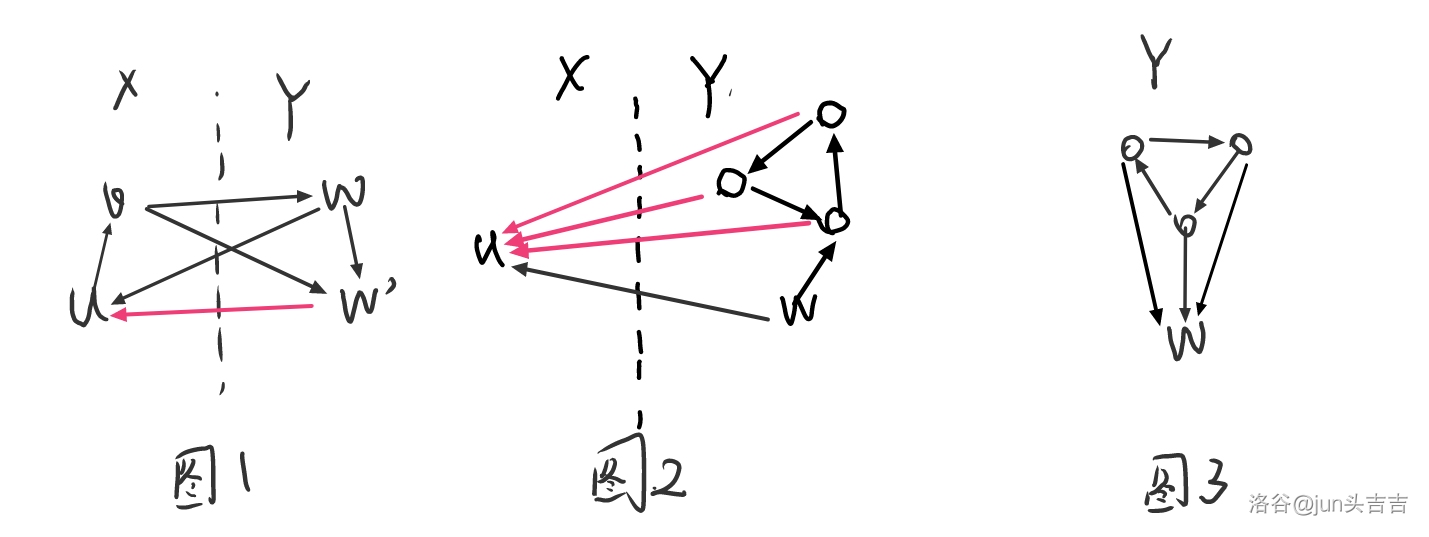
如图1所示,对于 $u\in X,w\in Y$,如果 $w\to u$,且 $w\to w'$,我们可以推出 $w'\to u$,否则就会构成 $H$。
**性质$\mathrm I.$** 如果 $u\in X,w\in Y$,如果 $w\to u$,则所有 $w$ 能走到的 $w'$ 都有 $w'\to u
然后一个显然的结论就是如果 Y 中有环,那么没有 w 能走到三元环,要么环缩点之后在 w 之前,三个点都和 w 右边。观察图2和图3不难发现两种情况必然会有 H 出现。
性质\mathrm {II}. 如果存在 u\in X,w\in Y,且 w\to u,那么 Y 也一定没有环。
然后我们保证了每个点至少有一个入度,所以取 u=x_1,至少存在一个 w 满足 w\to u,那么 Y 一定没有环。
结论\mathrm {II}. Y 是一个 DAG,存在一个 y_1,\dots,y_l ,满足若 i<j,则 y_i\to y_j。
结论\mathrm {III}. 当 Y 是 DAG 时 性质\mathrm I 可以变成若 y_j\to x_i,那么对于 j'\in[j,l],y_{j'}\to x_i。
然后发现如果 y_l\not\to x_1,那么不会有 y_i\to x_1,这与入度至少为 1 矛盾,因此:
结论\mathrm {IV}. y_l\to x_1 一定成立。
如图4,对于 2\le i\le k,如果 y_l\not\to x_i,那么对于 i'\in[i+1,k],如果 y_l\to x_{i'},那么显然就构成了 H,所以我们可以断定:
结论\mathrm V.如果 i'>i,y_l\not\to x_i,则 y_l\not\to x_{i'}。
对于我们找到最大的 t 满足 y_l\to x_t,那么对于 i\in [1,t],j\in[1,l-1],i'\in[i+1,t],如果 x_i\to y_j,那么已经有三元环了,如果 y_j\to x_{i'},我们又可以推出 y_l\to x_{i'},然后就构成了 H。由此,我们推出最后一条结论:
结论\mathrm {VI}. 对于 1\le i'<i\le t,如果 y_j\to x_i,则 y_j\to x_{i'}。
不难验证如果满足所有六条结论,则一定不存在 H。
如果我们画一个 k\times l 的网格图,y_j\to x_i 则将 (i,j) 涂黑,那么这个网格图满足:
- 如果 (i,j) 为黑,则所有1\le i'< i, (i',j) 也为黑
- 如果 (i,j) 为黑,则所有 j<j'\le l,(i,j') 也为黑
-
当然因为 v=x_k,所以 (k,j) 必然不能为黑。
没有度数就直接网格图上dp这一段阶梯状物即可。
有度数限制就相当于一行的黑色数量不能超过某个值,一列的白色数量不能超过某个值。这个不难在 \mathcal O(kl) 的复杂度求出。
然后求方案数就是钦定 v=1,枚举 k,l 网格图上填色。然后 x_1,\dots,x_{k-1},y_1,\dots,y_l 的方案数是 (n-1)!,其中 n 指的是当前子问题的规模。
复杂度 \mathcal O(N^4)。
代码
const int N=3e2+10;
int n,k;
mint C[N][N],fac[N];
mint dp[N][N];
mint calc(int k,int l,int up){
dp[0][0]=1;
for(int j=1;j<=l;j++){
mint sum=0;
for(int i=0;i<k;i++){
sum+=dp[j-1][i];
if((i-1)+(l-j+1)<=up&&(j-1)+(k-i)<=up)
dp[j][i]=sum;
else dp[j][i]=0;
}
}
mint ans=0;
for(int i=1;i<k;i++)ans+=dp[l][i];
return ans;
}
mint calc(int n,int k){
if(n==1)return 1;
mint ans=0;
for(int i=1;i<=k+1;i++)ans+=calc(i,n-i,k);
return ans*fac[n-1];
}
signed main(){
read(n,k,mod);
fac[0]=1;for(int i=1;i<N;i++)fac[i]=fac[i-1]*i;
for(int i=0;i<N;i++){
C[i][0]=1;
for(int j=1;j<=i;j++)C[i][j]=C[i-1][j-1]+C[i-1][j];
}mint ans=0;
for(int i=0;i<=k;i++)ans+=calc(n-i,k-i)*C[n][i]*fac[i];
writeln(ans.x);
}