【题解】P7569 「MCOI-05」粘液

· · 题解

题链

非常妙的分讨构造题。

Solution 1

n=1\ |\ m=1

此时只能一路冲到底，判一下与另一个的大小关系即可。

Solution 2

k\ge n\ |\ k\ge m

我们就可以对短的那一维，每次冲到底，然后换下一行/列。

inline void work_1()
{
    if(n==1){if(k<m){puts("NO");return;}puts("YES");for(int i=1;i<m;i++)putchar('R');puts("");puts("1 1");return;}
    puts("YES");for(int i=1;i<=m;i++){for(int j=1;j<n;j++)putchar((i&1)?'D':'U');if(i!=m)putchar('R');}puts("");
    printf("%d %d\n",1,1);return;
}
inline void work_2()
{
    if(m==1){puts("NO");return;}
    puts("YES");for(int i=1;i<=n;i++){for(int j=1;j<m;j++)putchar((i&1)?'R':'L');if(i!=n)putchar('D');}puts("");
    printf("%d %d\n",1,1);return;
    return;
}

这前两个 Solution 判完后，显然 k\le 2 无解。

可以自己手玩一下。

Solution 3

k\ge 5

此时有一种构造，就是直接每次消 2/3 行/列，其中前面的 2,3 取决于另一维的奇偶性。

具体的，拿消列举例，是这样的两个图形：

行为奇数时：

行为偶数时：

会注意到这样之后会变成一个规模更小的子问题。

递归的边界条件是 m=2|3，此时按照前面两个 Solution 的跑法即可。

但是涉及到每次切换子问题会有一个 前面积攒 的连续走的步数，当 k\ge 5 时，最坏的情况也是能接受的。

大家可以手玩一下。

这里涉及到子问题，会注意到如果写一堆 if 语句来判断当前出发点是在矩阵的哪个角落会非常地屎。

我是在跑的时候默认出发点在左上角，但是存储一下当前的反转状态，然后在输出的时候转化一下就好。


struct gyq
{
    char c[4];
    // 0 1 2 3
    // 上下左右
    inline void init(){c[0]='U';c[1]='D';c[2]='L';c[3]='R';return;}
    inline void change(int typ)
    {
        if(typ==1||typ==3)jh(c[2],c[3]);
        if(typ==2||typ==3)jh(c[0],c[1]);
        return;
        //typ 0 1 2 3 分别对应左上，右上，左下，右下
    }
}tp[4];

inline void work_stp(int n,int m,int typ)
{
    if(n<=3){for(int i=1;i<=m;i++){for(int j=1;j<n;j++)putchar(tp[typ].c[i&1]);if(i!=m)putchar(tp[typ].c[3]);}return;}
    if(m<=3){for(int i=1;i<=n;i++){for(int j=1;j<m;j++)putchar(tp[typ].c[2+(i&1)]);if(i!=n)putchar(tp[typ].c[1]);}return;}
    if(n&1)
    {
        for(int i=1;i<=n;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[2+(i&1)]);if(i!=n)putchar(tp[typ].c[1]);}
        putchar(tp[typ].c[3]);
        int nxt;if(typ==0)nxt=2;if(typ==1)nxt=3;if(typ==2)nxt=0;if(typ==3)nxt=1;work_stp(n,m-2,nxt);
        return;
    }
    if(m&1)
    {
        for(int i=1;i<=m;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[i&1]);if(i!=m)putchar(tp[typ].c[3]);}
        putchar(tp[typ].c[1]);
        int nxt;if(typ==0)nxt=1;if(typ==1)nxt=0;if(typ==2)nxt=3;if(typ==3)nxt=2;work_stp(n-2,m,nxt);
    }
    return;
}

这里是暴力跑奇的，如果初始 n,m 都为偶，就跑一遍前面说的那种就可以调用这个函数了。

Solution 4

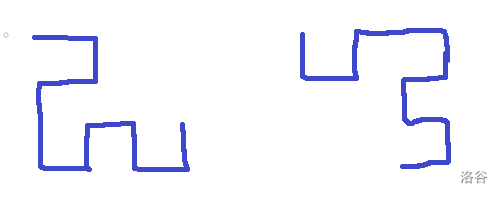
并没有这个 subtask 但是这个部分非常关键。 因为会发现我们的瓶颈在于：递归到最后的边界时，前面转化子问题时积攒的步数会和边界时暴力冲到底的步数相加。 最坏的情况，就是前面跑了一个 **行为奇数** 的子问题转化，积攒了两步到达当前子问题，然后列还剩 $3$，只能暴力跑，相加得到的最大连续步数为 $4$。 此时 $k\ge 5$ 才能有解。 但是如果行列都是偶数时，我们存在一种更优秀的构造： ![](https://cdn.luogu.com.cn/upload/image_hosting/rfo2wobf.png) 这样每次消去两行两列。 为什么要这两种都画呢？因为它们都有用。当 $n\ge m$ 时，我们会调用第一种跑法，这样最后暴力跑的时候就不会有步数的相加。第二种跑法对应另一种 Case。 这样可以达到 $k\ge 3$ 时都有解。 $k\le 2$ 时无解已经判过了。 --- ```cpp inline void work_zjj(int n,int m,int typ) { if(m==2){for(int i=1;i<=n;i++){for(int j=1;j<m;j++)putchar(tp[typ].c[2+(i&1)]);if(i!=n)putchar(tp[typ].c[1]);}return;} for(int i=1;i<=n-2;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[2+(i&1)]);if(i!=n)putchar(tp[typ].c[1]);} putchar(tp[typ].c[1]);putchar(tp[typ].c[3]);putchar(tp[typ].c[0]);putchar(tp[typ].c[3]); for(int i=3;i<=m;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[i&1]);if(i!=m)putchar(tp[typ].c[3]);} putchar(tp[typ].c[0]);int nxt=3-typ;work_zjj(n-2,m-2,nxt); return; } inline void work_gyq(int n,int m,int typ) { if(n==2){for(int i=1;i<=m;i++){for(int j=1;j<n;j++)putchar(tp[typ].c[i&1]);if(i!=m)putchar(tp[typ].c[3]);}return;} for(int i=1;i<=m-2;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[i&1]);if(i!=m)putchar(tp[typ].c[3]);} putchar(tp[typ].c[3]);putchar(tp[typ].c[1]);putchar(tp[typ].c[2]);putchar(tp[typ].c[1]); for(int i=3;i<=n;i++){for(int j=1;j<2;j++)putchar(tp[typ].c[2+(i&1)]);if(i!=n)putchar(tp[typ].c[1]);} putchar(tp[typ].c[2]);int nxt=3-typ;work_gyq(n-2,m-2,nxt); return; } ``` --- ### Solution 5 $n,m$ 无限制。 会注意到：我们只要能够转移到 $n,m$ 都为偶数的子问题，就可以轻松地解决此题了。 回想到前面 Solution 3 中消 3 行/列 的操作，它可以改变另一维的奇偶性。 那么对于 $n,m$ 只有一个奇数的情况，我们就可以跑一遍这个得到双偶的 Case。 如果都是奇数呢？ 我们可以出发点选择 $(3,1)$，然后跑一遍： ![](https://cdn.luogu.com.cn/upload/image_hosting/ax0shmh3.png) 这样就可以把 $m$ 变成偶数，然后再跑一遍 Solution 3 中的方法把 $n$ 也变成偶数。 于是本题就**轻松**做完了（ --- ```cpp inline void work_6() { puts("YES"); if(m&1) { if(n&1) { for(int i=1;i<=n-2;i++){for(int j=1;j<3;j++)putchar(tp[0].c[3-(i&1)]);if(i!=n)putchar(tp[0].c[1]);} for(int i=1;i<=3;i++){for(int j=1;j<2;j++)putchar(tp[0].c[i&1]);putchar(tp[0].c[3]);} m-=3; for(int i=1;i<=m-2;i++){for(int j=1;j<3;j++)putchar(tp[2].c[i&1]);if(i!=m)putchar(tp[2].c[3]);} for(int i=1;i<=3;i++){for(int j=1;j<2;j++)putchar(tp[2].c[2+(i&1)]);putchar(tp[2].c[1]);} n-=3;{if(n>=m)work_zjj(n,m,3);else work_gyq(n,m,3);} puts("");puts("1 3"); } else { for(int i=1;i<=n-2;i++){for(int j=1;j<3;j++)putchar(tp[0].c[2+(i&1)]);if(i!=n)putchar(tp[0].c[1]);} for(int i=1;i<=3;i++){for(int j=1;j<2;j++)putchar(tp[0].c[i&1]);putchar(tp[0].c[3]);} m-=3; if(n>=m)work_zjj(n,m,2);else work_gyq(n,m,2); puts("");puts("1 1"); } return; } if(n&1) { for(int i=1;i<=m-2;i++){for(int j=1;j<3;j++)putchar(tp[0].c[i&1]);if(i!=m)putchar(tp[0].c[3]);} for(int i=1;i<=3;i++){for(int j=1;j<2;j++)putchar(tp[0].c[2+(i&1)]);putchar(tp[0].c[1]);} n-=3;if(n>=m)work_zjj(n,m,1);else work_gyq(n,m,1);puts("");puts("1 1");return; } else {if(n>=m)work_zjj(n,m,0);else work_gyq(n,m,0);}puts("");puts("1 1");return; return; } ```