P5037 Dijkstra神奇优化
GalwayGirl
·
·
题解
题意简述
初看题目,觉得很容易,就是让你将除了 1 之外的两两互质的点建边,边权取决于出发点,问从 s 到 t 的最短路。
Solution
考虑本题与其他题目不同的地方,它的边权就是出发点。
再考虑一下 Dijkstra 的核心思想,就是贪心的将最短距离放入堆中,再提出来对终点进行松弛操作。对两种不同的边权画图分析。
1. 两点之间边权给出。
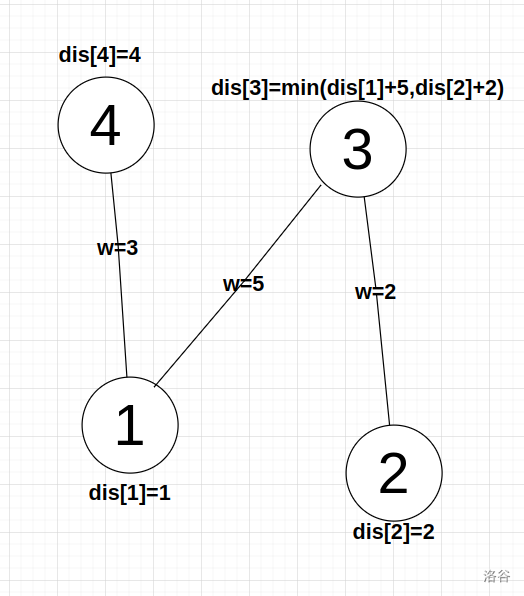
可以看到节点 1 和 节点 2 对 3 进行松弛,然后 1 又对 4 进行松弛,因为一个点与不同点的边权的差异性,导致每次都要将点提出来更新其他点。
2. 边权取决与点
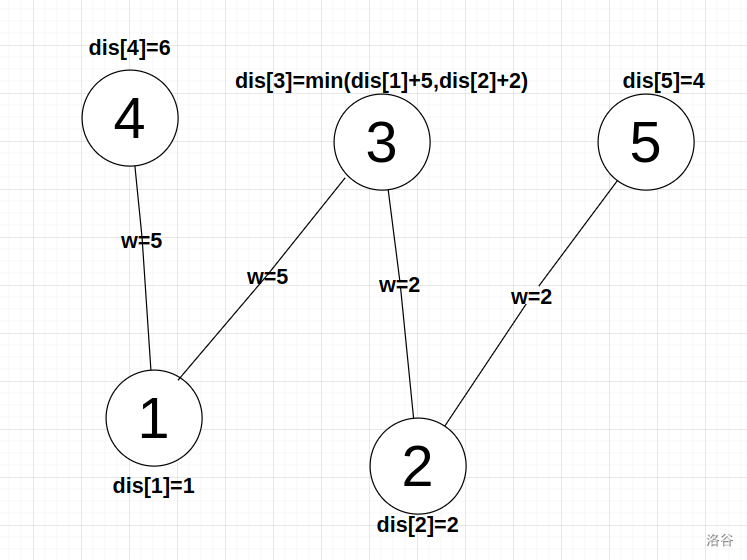
因为每个点到其他点的边权是相同的,所以上图与下图是等价的。
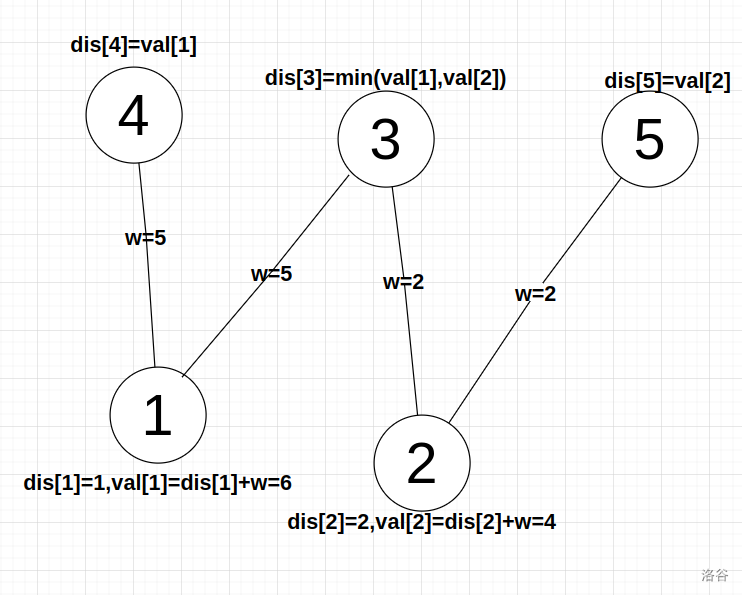
可以发现当点到其他点边权相同时,点权加上边权为定值,所以在放入堆中时可以将点权加边权作为排序关键字,进行松弛操作时提出来的点一定是最优的,直接赋值即可,具体操作见此处代码。
```cpp
S=read();T=read();
for(int i=1;i<=n;i++)w[i]=read(),dis[i]=1e18,vis[i]=false;
priority_queue<hh>q;
q.push({S,w[S]});
dis[S]=0;
while(!q.empty()){
int now=q.top().id;
long long val=q.top().val;
q.pop();
if(vis[now])continue;
vis[now]=true;
for(int i=head[now];i;i=edge[i].next){
int v=edge[i].to;
dis[v]=val;
if(v==T){
printf("%lld\n",dis[T]);
return;
}
q.push({v,dis[v]+w[v]});
}
}
```
所以在写类似优化的题时,一定要了解算法核心才能想办法优化。
最后贴上代码。
```cpp
#include<bits/stdc++.h>
using namespace std;
const int M=3e7,N=4600;
int t,n,c,head[N],S,T,w[N];
long long dis[N];
bool vis[N];
inline int read(){
int x=0,w=1;char ch=0;
while(ch<'0'||ch>'9'){
if(ch=='-')w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+ch-'0';
ch=getchar();
}
return x*w;
}
struct xzh{
int next,to;
}edge[M*2];
struct hh{
int id;
long long val;
bool operator <(const hh&x)const{
return x.val<val;
}
};
void add(int u,int v){
c++;
edge[c].next=head[u];
edge[c].to=v;
head[u]=c;
}
int gcd(int a,int b){
if(b==0)return a;
return gcd(b,a%b);
}
void pre(){
for(int i=2;i<=n;i++){
for(int j=i;j<=n;j++){
if(gcd(i,j)==1)add(i,j),add(j,i);
}
}
}
void solve(){
S=read();T=read();
for(int i=1;i<=n;i++)w[i]=read(),dis[i]=1e18,vis[i]=false;
priority_queue<hh>q;
q.push({S,w[S]});
dis[S]=0;
while(!q.empty()){
int now=q.top().id;
long long val=q.top().val;
q.pop();
if(vis[now])continue;
vis[now]=true;
for(int i=head[now];i;i=edge[i].next){
int v=edge[i].to;
dis[v]=val;
if(v==T){
printf("%lld\n",dis[T]);
return;
}
q.push({v,dis[v]+w[v]});
}
}
}
int main(){
t=read();n=read();
pre();
while(t--)solve();
}
```