题解 P8114【[Cnoi2021]六边形战士】
whiteqwq
·
·
题解
P8114 [Cnoi2021]六边形战士 解题报告:
更好的阅读体验
题意
给定一个三条边分别有 a,b,c 个六边形的六边形网络,求网络上所有边组成的二分图的完美匹配数量。
## 分析
非人力可及的巨大神仙题,膜拜 bzy。
考虑将匹配按照朝向分成三类:平、朝上、朝下,将三种匹配按照类型染上不同的颜色,然后考察其对应的三角形网络:

(图来自 [Solara570-在二维世界中解决看似立体的平面问题](https://www.bilibili.com/video/av200522733))
可以证明染色方法可以与平面的立方体凸堆叠一一对应。
考察高度 $v$ 与高度 $v+1$ 的分界线,将这 $c$ 条分界线画出来,可以发现路径 $i$ 可以与路径 $i+1$ 重叠,但是不能越过。
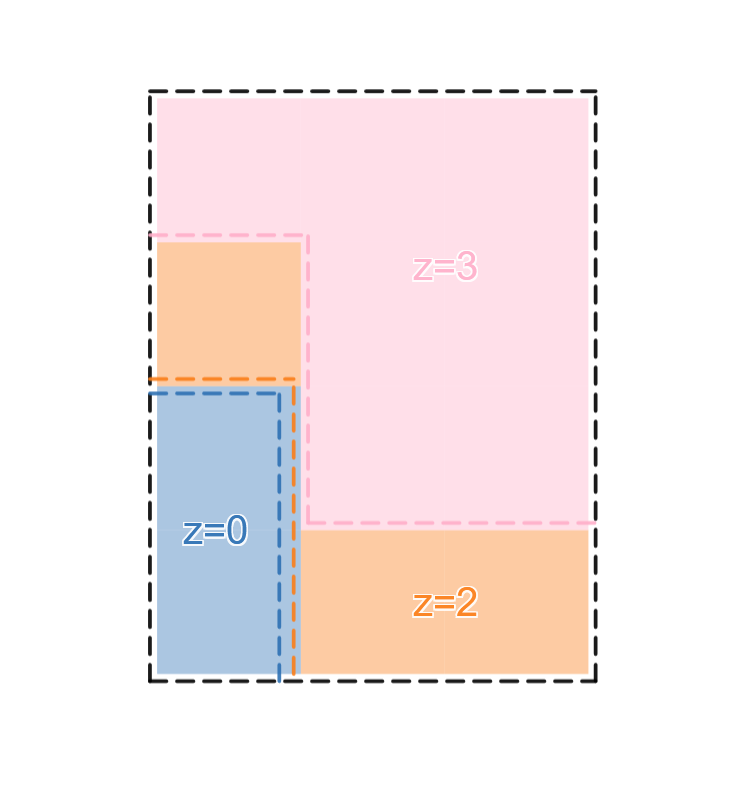
(图,以及下面的图都来自官方题解)
将第 $i$ 条路径向右上平移 $i-1$ 格,可以得到一个新的网格,可以发现此时已经转化成 LGV 能解决的问题了,直接列出矩阵,求行列式即可做到立方复杂度了。
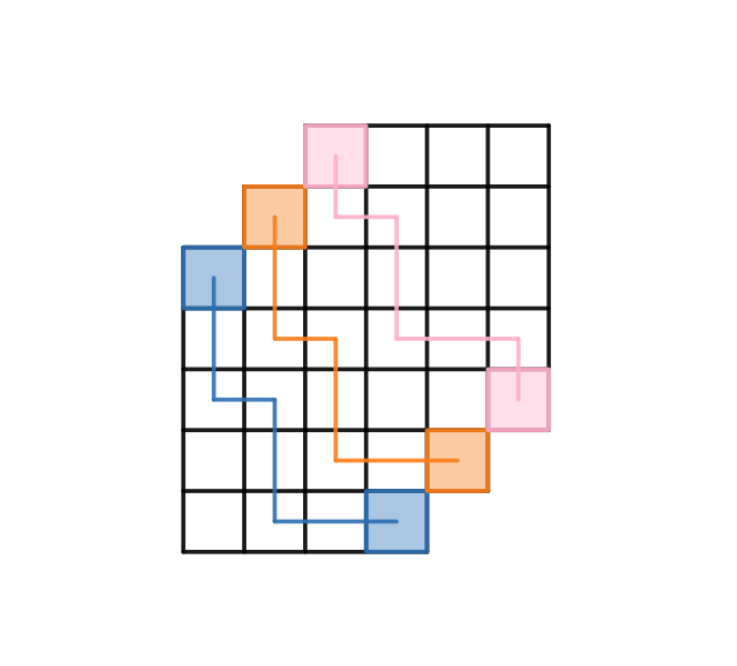
列出矩阵,容易发现每个出发点到每个结束点的距离都是 $a+b$,且第 $i$ 个出发点和第 $j$ 个到达点的横向距离为 $a+(x-y)$:
$$ans=\det(M)\\M=\begin{bmatrix}{a+b\choose a}&{a+b\choose a-1}&\cdots&{a+b\choose a+1-c}\\{a+b\choose a+1}&{a+b\choose a}&\cdots&{a+b\choose a+2-c}\\\vdots&\vdots&\ddots&\vdots\\{a+b\choose a+c-1}&{a+b\choose c-2}&\cdots&{a+b\choose a}\end{bmatrix}$$
下面就是一些 dirty work 了:
$$\det(M)=\det(M')\times\prod_{i=1}^c\frac{(a+b)!}{(a+c-i))!(b+i-1)!}\\=\det(M'')\times\prod_{i=1}^c\frac{(a+b)!}{(a+c-i))!(b+i-1)!}\times(-1)^{\frac{c(c-1)}{2}}\\M_{i,j}'=\prod_{k=j+1}^c(a+k-i)\prod_{k=2}^j(b+i-k+1)\\M''_{i,j}=\prod_{k=j+1}^c(a+k-i)\prod_{k=2}^j(k-b-1-i)$$
根据题面提供的公式 Krattenthaler’s formula:
$$\det(\prod_{k=2}^j(x_i+a_k)\prod_{k=j+1}^m(x_i+b_k))_{i,j=1}^n=\prod_{1\leqslant i<j\leqslant n}(x_i-x_j)\prod_{2<i\leqslant j\leqslant n}(a_i-b_j)$$
$$\det(M'')=\prod_{1\leqslant i<j<c}(j-i)\prod_{2\leqslant i\leqslant j\leqslant c}(a+b+j-i-1)$$
$$\det(M)=\prod_{1\leqslant i<j<c}(i-j)\prod_{2\leqslant i\leqslant j\leqslant c}(a+b+j-i-1)\times\prod_{i=1}^c\frac{(a+b)!}{(a+c-i))!(b+i-1)!}\times(-1)^{\frac{c(c-1)}{2}}\\=\prod_{i=1}^{c-1}(i!)\prod_{i=1}^{c-1}(a+b+i)^{\underline i}\prod_{i=1}^c\frac{(a+b)!}{(a+c-i)!(b+i-1)!}\\=\prod_{i=1}^{c-1}(i!)\prod_{i=1}^{c-1}\frac{(a+b+i)!}{(a+b)!}\prod_{i=1}^c(a+b)!\prod_{i=1}^c\frac{1}{(a+c-i)!}\prod_{i=1}^c\frac{1}{(b+i-1)!}\\=\prod_{i=1}^{c-1}(i!)((a+b)!\times\prod_{i=1}^c(a+b+i)!)\frac{\prod_{i=0}^{a-1}(i!)}{\prod_{i=0}^{a+c-1}(i!)}\frac{\prod_{i=0}^{b-1}(i!)}{\prod_{i=0}^{b+c-1}(i!)}\\=\frac{H(a)H(b)H(c)H(a+b+c)}{H(a+b)H(b+c)H(a+c)}\\H(x)=\prod_{i=0}^{x-1}(i!)$$
然后就可以线性了。
## 代码
```
#include<stdio.h>
const int maxn=3000005,mod=998244353;
int a,b,c;
int fac[maxn],ffac[maxn];
int ksm(int a,int b){
int res=1;
while(b){
if(b&1)
res=1ll*res*a%mod;
a=1ll*a*a%mod,b>>=1;
}
return res;
}
int main(){
fac[0]=ffac[0]=1;
for(int i=1;i<maxn;i++)
fac[i]=1ll*fac[i-1]*i%mod,ffac[i]=1ll*ffac[i-1]*fac[i]%mod;
scanf("%d%d%d",&a,&b,&c);
printf("%d\n",1ll*ffac[a-1]*ffac[b-1]%mod*ffac[c-1]%mod*ffac[a+b+c-1]%mod*ksm(ffac[a+b-1],mod-2)%mod*ksm(ffac[a+c-1],mod-2)%mod*ksm(ffac[b+c-1],mod-2)%mod);
return 0;
}
```