泪水与凋零的花瓣是同样的色彩 | 题解:P6646 [CCO2020] Shopping Plans
Petit_Souris
·
·
题解
好像在好久以前我在模拟赛中这个题取得了 eps 分的好成绩,今天一看感觉还是不会做,一年了没有长进啊。不过这种题原来是有比较套路化的思考方式的,学习到了。
对于这类问题的一个通用想法是,设计一种转移,构成一棵外向树,且父亲节点权值小于等于儿子节点权值,这样到达每个点的路径唯一,直接维护一个堆,每次找到最小的点,再扩展所有儿子就是正确的了。
首先考虑 m=1,l=r 怎么做。先从小到大排序,固定起始状态为 [1,l]。设计这样一种扩展方式:
从右到左,依次将每个元素右移非负整数位。
这样我们可以保证转移到每个状态的方式有且仅有一种,且每次代价不会变小。
但是每次右移多位,时间复杂度就爆了。这里有一个很重要的思想:分步转移。你也可以理解为,把一棵多叉树的儿子从左到右连成一条链。
所以现在我们的转移长这样:
-
把当前正在转移的元素右移一位;
-
开始转移下一个元素。
因此一个状态应当形如 (x,y,z),表示目前正在转移第 x+1 个元素([1,x] 固定前缀不动),第 x+1 个元素正在 y 的位置,上一个右移的元素限制第 x+1 个元素不能越过 z(也就是上个元素移到了 z+1)。
第一种转移就是 (x,y,z)\to (x,y+1,z),第二种转移就是 (x,y,z)\to (x-1,x,y-1)。可以做到 \mathcal O(\log n) 扩展一个答案。
接下来考虑 $m>1,l=r=1$ 的情况。我们还是要设计一种转移,使得满足一开始说的条件。有了上一部分的经验,我们发现**按顺序转移**是个很好的事情,也就是移动了 $x$ 的指针之后就不再移动 $x-1$ 及以前的指针了。
所以我们的转移还是:
- 把当前正在转移的元素右移一位;
- 开始转移下一个元素。
但是这样有一个问题:你每次做第二种转移,移动不同距离的元素应当同时被加入堆里。这令人有些火大,不过我们不妨再次利用刚刚的“多叉树转二叉树”技巧,把转移拉成一条链。
那么现在的转移形如:
- 把当前正在转移的元素右移一位;
- 开始转移下一个元素,把下一个元素右移一位;
- **当前元素选择的是次小的方案**。撤销当前的选择,换回最小的方案,再开始转移下一个元素,把下一个元素右移一位。
可以这样理解:
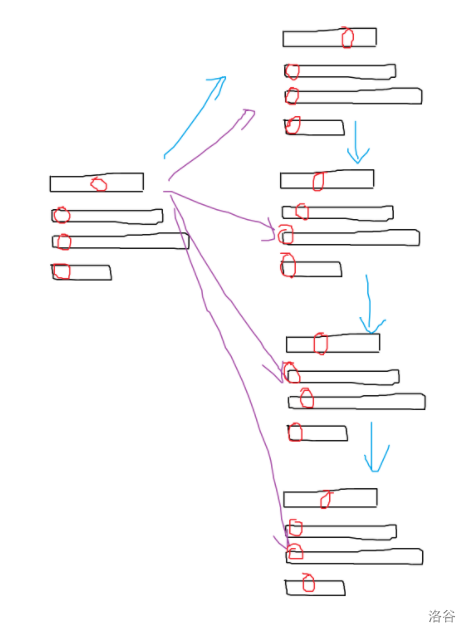
其中红圈表示目前选到的元素,紫色箭头表示原转移,蓝色箭头表示新转移。为了使新转移合法,我们需要让代价不降,因此将所有序列按照次小值减最小值从小到大排序。
最后考虑 $m>1$,$l,r$ 任意的情况。实际上就是在主体上使用 $m>1,l=r=1$ 的做法,在每个序列内部求解第 $k$ 小解的时候用 $m=1$ 的做法。总时间复杂度 $\mathcal O(n\log n)$。
```cpp
#include<bits/stdc++.h>
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
#define pii pair<ll,ll>
#define rep(i,a,b) for(ll i=(a);i<=(b);++i)
#define per(i,a,b) for(ll i=(a);i>=(b);--i)
using namespace std;
bool Mbe;
ll read(){
ll x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void write(ll x){
if(x<0)putchar('-'),x=-x;
if(x>9)write(x/10);
putchar(x%10+'0');
}
const ll N=2e5+9,INF=1e16;
ll n,m,K,L[N],R[N],id[N];
vector<ll>a[N],b[N];
struct Nodeq{
ll pre,ptr,rg,val;
//pre 是目前还没动的前缀长度(也就是现在在动 pre+1)
//ptr 是目前移到哪里了
//rg 是右边界(上一个移动的数对下一个数的限制)
};
bool operator<(const Nodeq&a,const Nodeq&b){
return a.val<b.val;
}
bool operator>(const Nodeq&a,const Nodeq&b){
return a.val>b.val;
}
struct DS{
vector<ll>ret,a;
ll L,R,now;
priority_queue<Nodeq,vector<Nodeq>,greater<Nodeq> >q;
void Expand(){
if(q.empty())return ret.push_back(INF),void();
Nodeq now=q.top();q.pop();
ll pre=now.pre,ptr=now.ptr,rg=now.rg,val=now.val;
ret.push_back(val);
//转移 1:目前是固定的初始状态,多加入一个数
if(rg==(ll)a.size()-1&&ptr==pre+1&&ptr+1<R)q.push({pre+1,ptr+1,rg,val+a[ptr+1]});
//转移 2:将现在的数右移一位
if(ptr>=0&&ptr+1<=rg)q.push({pre,ptr+1,rg,val-a[ptr]+a[ptr+1]});
//转移 3:结束移动当前的数,让下个数移动
if(pre>=0&&pre+1<ptr)q.push({pre-1,pre+1,ptr-1,val-a[pre]+a[pre+1]});
}
ll operator [](ll x){
while(x>=(ll)ret.size())Expand();
return ret[x];
}
void Build(const vector<ll>&_a,const ll&_L,const ll&_R){
L=_L,R=_R,a=_a;
if(L>(ll)a.size())return ret={INF,INF},void();
R=min(R,(ll)a.size());
ll s=accumulate(a.begin(),a.begin()+L,0ll);
q.push({L-2,L-1,(ll)a.size()-1,s});
Expand(),Expand();
}
}D[N];
struct Node{
ll ptr,lst,val;
//ptr 是目前扩展的位置
//lst 表示上一位选的是第几小的方案
};
bool operator<(const Node&a,const Node&b){
return a.val<b.val;
}
bool operator>(const Node&a,const Node&b){
return a.val>b.val;
}
priority_queue<Node,vector<Node>,greater<Node> >q;
bool Med;
int main(){
cerr<<fabs(&Med-&Mbe)/1048576.0<<"MB\n";
n=read(),m=read(),K=read();
rep(i,1,n){
ll x=read(),y=read();
a[x].push_back(y);
}
rep(i,1,m)L[i]=read(),R[i]=read(),sort(a[i].begin(),a[i].end()),id[i]=i;
rep(i,1,m)D[i].Build(a[i],L[i],R[i]);
rep(i,1,m){
if(D[i][0]==INF){
while(K--)puts("-1");
return 0;
}
}
sort(id+1,id+m+1,[&](ll x,ll y){
return D[x][1]-D[x][0]<D[y][1]-D[y][0];
});
ll mnc=0;
rep(i,1,m)mnc+=D[i][0];
q.push({0,0,mnc});
ll C=0;
while(!q.empty()&&C<K){
Node now=q.top();q.pop();
ll ptr=now.ptr,lst=now.lst,val=now.val;
if(val>=INF)break;
C++,write(val),putchar('\n');
//转移 1:将当前位置右移
if(ptr)q.push({ptr,lst+1,val-D[id[ptr]][lst]+D[id[ptr]][lst+1]});
//转移 2:将指针右移,下个位置右移
if(ptr<m)q.push({ptr+1,1,val-D[id[ptr+1]][0]+D[id[ptr+1]][1]});
//转移 3:目前选的是次小值,撤销这位变成最小值,转移到下一位对应的兄弟节点
if(ptr<m&&lst==1)q.push({ptr+1,1,val+D[id[ptr]][0]-D[id[ptr]][1]+D[id[ptr+1]][1]-D[id[ptr+1]][0]});
}
while(C<K)puts("-1"),C++;
cerr<<"\n"<<clock()*1.0/CLOCKS_PER_SEC*1000<<"ms\n";
return 0;
}
```