inline void insert(char *ss) {
int len = strlen(ss + 1), pos = 1;
for (int i = 1; i <= len; i ++) {
int c = ss[i] - 'a';
if (! trie[pos][c])
trie[pos][c] = ++ tot;
pos = trie[pos][c];
}
cnt[pos] ++;
}
现在我们要像 KMP 一样建一个 nxt 数组, 但是这次我们不叫 nxt,叫 fail 了。
那么这个家伙的意思就是:如果说从 root 到 i 的串我们设为 A,从 root 到 j 的串我们称为 B,则 B 是 A 的最长后缀。
先看看我们的字典树:
那么我们便开始找 fail 吧!
很明显,由图可知,根节点所有的孩子的 fail 边所指向的点都是根节点。
那么我们是不是可以这样:
把所有根节点的儿子的 fail 先预处理出来,
然后接下来开始匹配,
我们先遍历到这个 a 的一个儿子即 k,
明显的,他没有一个是能够匹配的上的,于是他的 fail 边只能指向根节点。
如图:
绿色的即为第三层的 fail 边,第二层的 fail 边即为蓝色的。
接下来我们遍历 b 的儿子即为 a:
那么明显的有一个 a,所以这个 fail 边便可以连向 a。
看图:
那我们再来遍历 c 的儿子,即为 a,
那么我们同样的还能找到那个 a。
再来看 y,
没有与之匹配的 fail 边,
便只能连向根节点。
如图:
然后接下来便可以遍历 k 的儿子就是 i:
明显,i 也没有相同的字母, fail 边还是指向根节点。
再来看 k 的另一个儿子 o,明显的,我们也只能指向根节点。
图在下方,
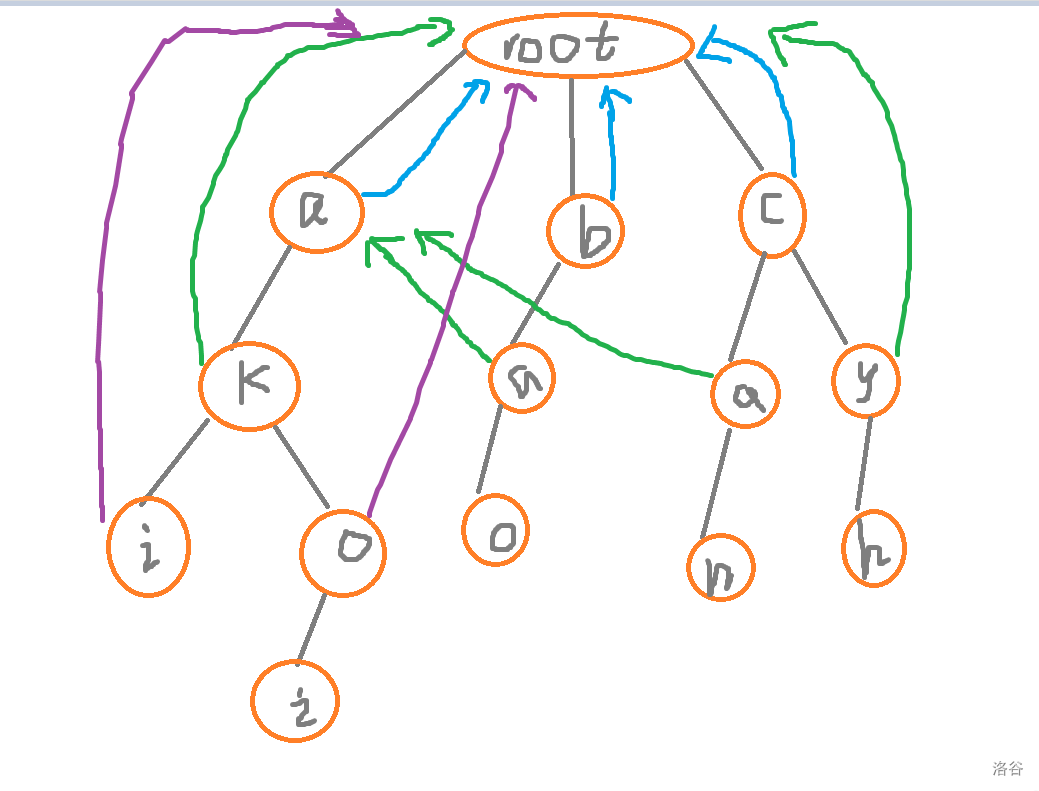
然后我们再来看这个 $a$ 的儿子,就是 $o$,
我们从 $o$ 的爸爸即为 $a$ 的 $fail$ 看,其实可以发现是没有的。
所以还是连向根节点。
那么这到底是什么情况呢?
偶然?
我们看看之前所有连接的:
如果我们把 $pos$ 设为当前要求的 $fail$ 的点,那么是不是上面所有的点的 $fail$ 边都可以看成 $pos$ 他爹的$fail$ 边有无这个儿子 $k$。
若有,$fail$ 边连向 $k$;
若没有,连向根节点。
并且,我刚刚遍历是不是按层遍历,即为 $bfs$。
所以我们可以用队列实现:
一个个儿子遍历过去,碰到的有这个儿子(真儿子),便可查询。
但是如果没有呢(假儿子)?
好办,**把连接假儿子的边设为他父亲这个点的 $fail$ 边所指向的与其相同字母的儿子**。
代码就出来了:
```
inline void bfs() {
queue <int> q;
for (int i = 0; i < 26; i ++) {
int pos = trie[1][i];//根节点的儿子(包括真假)
if (pos) {//真儿子
fail[pos] = 1;//fail数组指向根节点
q.push(pos);//入队
}
}//把根节点的儿子设为根节点,方便查询,并把他们入队
while (! q.empty()) {//开始匹配
int u = q.front();//取出队头
q.pop();//弹出
for (int i = 0; i < 26; i ++) {//一个个儿子遍历
int pos = trie[u][i];//u 的为i字母的儿子(包括真假)
if (pos) {//如果u的这个儿子是真儿子
fail[pos] = trie[fail[u]][i];//就把u这个点的儿子的fail边设置为u的fail边的那个同样的儿子
if (! fail[pos])
fail[pos] = 1;
q.push(pos);//入队
} else//如果是假儿子
trie[u][i] = trie[fail[u]][i];// 就把u的连接假儿子的边设为u这个点的fail边所指向的与其相同字母的儿子
}
}
}
```
接下来是查询,
既然是查询哪些在文本中出现且相同的位置不同即可。
我们在每次查询前跳到 $fail$ 边即可,
所以查询也是极其简单的。
代码:
```
inline int find(char *ss) {
int len = strlen(ss + 1), pos = 1, sum = 0;
for (int i = 1; i <= len; i ++) {
int c = ss[i] - 'a';
int u = trie[pos][c];
while (u&& cnt[u] != -1) {//有这个儿子且没被搜过
sum += cnt[u];//加上答案
cnt[u] = -1;//标记
u = fail[u]; //跳到fail边
}
pos = trie[pos][c];//向下继续搞
}
return sum;
}
```
于是乎,就解决完毕了。
完整代码:
```cpp
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
const int N = 1e6 + 7;
using namespace std;
char s[N];
int n, tot = 1;
struct AC {
int trie[N][27];
int cnt[N];
int fail[N];
inline void insert(char *ss) {
int len = strlen(ss + 1), pos = 1;
for (int i = 1; i <= len; i ++) {
int c = ss[i] - 'a';
if (! trie[pos][c])
trie[pos][c] = ++ tot;
pos = trie[pos][c];
}
cnt[pos] ++;
}//构建trie 树
inline void bfs() {
queue <int> q;
for (int i = 0; i < 26; i ++) {
int pos = trie[1][i];//根节点的儿子(包括真假)
if (pos) {//真儿子
fail[pos] = 1;//fail数组指向根节点
q.push(pos);//入队
}
}//把根节点的儿子设为根节点,方便查询,并把他们入队
while (! q.empty()) {//开始匹配
int u = q.front();//取出队头
q.pop();//弹出
for (int i = 0; i < 26; i ++) {//一个个儿子遍历
int pos = trie[u][i];//u 的为i字母的儿子(包括真假)
if (pos) {//如果u的这个儿子是真儿子
fail[pos] = trie[fail[u]][i];//就把u这个点的儿子的fail边设置为u的fail边的那个同样的儿子
if (! fail[pos])
fail[pos] = 1;
q.push(pos);//入队
} else//如果是假儿子
trie[u][i] = trie[fail[u]][i];// 就把u的连接假儿子的边设为u这个点的fail边所指向的与其相同字母的儿子
}
}
}
inline int find(char *ss) {
int len = strlen(ss + 1), pos = 1, sum = 0;
for (int i = 1; i <= len; i ++) {
int c = ss[i] - 'a';
int u = trie[pos][c];
while (u&& cnt[u] != -1) {//有这个儿子且没被搜过
sum += cnt[u];//加上答案
cnt[u] = -1;//标记
u = fail[u]; //跳到fail边
}
pos = trie[pos][c];//向下继续搞
}
return sum;
}
} ac;
int main() {
freopen(".in", "r", stdin);
freopen(".out", "w", stdout);
cin >> n;
for (int i = 1; i <= n; i ++) {
scanf("%s", s + 1);
ac.insert(s);
}
ac.bfs();
scanf("%s", s + 1);
cout << ac.find(s) << endl;
return 0;
}
```
请勿直接抄(注意 freopen)。
$Atlantic$.