CF2125E Sets of Complementary Sums 题解
蒟蒻君HJT
·
·
题解
考虑所有 $c[i]=1$ 次的情况。此时可以发现 $\displaystyle\sum b[i]=\frac{\displaystyle\sum d[i]}{n - 1}$。并且只要 $\displaystyle\frac{\displaystyle\sum d[i]}{n - 1}$ 为整数且大于 $d[1]$,就一定能通过其分别减去所有 $d[i]$,来解出合法的 $b[1]\sim b[n]$。
$c[i]\neq 1$ 的情况,也可以找到类似的式子:$\displaystyle\sum b[i]c[i]=\frac{\displaystyle\sum c[i]d[i]}{(\displaystyle\sum c[i]) - 1}$(怎么理解?一共有 $\displaystyle\sum c[i]$ 个数,求出 $\displaystyle\sum c[i]$ 个和,每个和对应缺掉其中一个数,所以加起来的和每个数出现了 $(\displaystyle\sum c[i]) - 1$ 次)。只要 $\displaystyle\frac{\displaystyle\sum c[i]d[i]}{(\displaystyle\sum c[i]) - 1}=d[1]+t$,$t$ 为正整数即可。
以上式子我们可以发现 $d[1]$ 的存在是特殊的,所以将 $d[1]$ 与其他 $d[i]$ 分离化简,得到 $d[1]+t(1-c[1])=\displaystyle\sum_{i=2}^{n} (d[1]-d[i]+t)c[i]$,左边有上界 $d[1]$,右边有下界 $\displaystyle\sum_{i=2}^{n} (d[1]-d[i]+1)$,那么是否只要满足 $d[1]\geq \displaystyle\sum_{i=2}^{n} (d[1]-d[i]+1)$ 就可以了呢?确实如此,在此情况下,我们可以通过令 $c[2]\sim c[n]$ 都为 $1$,$c[1]$ 为 $2$,取合适的正整数 $t$ 使得 $d[1]+t(1-c[1])=\displaystyle\sum_{i=2}^{n} (d[1]-d[i]+1)c[i]$ 成立。
现在问题转化为了求有多少组 $x\geq d[1]>d[2]>\cdots >d[n]\geq 1$ 满足 $d[1]\geq \displaystyle\sum_{i=2}^{n} (d[1]-d[i]+1)$。注意到 $d[i]$ 都比较接近 $d[1]$,记 $e[i]=d[1]-d[i]+1,2\leq i\leq n$,则有 $2\leq e[2]<e[3]<\cdots <e[n]\leq d[1]\leq x$。又可以转化为选出 $n-1$ 个 $[2,x]$ 中不同的数,若他们的和为 $s$,则能贡献 $x-s+1$ 种方案($d[1]$ 的方案数),因此只需要求出选出 $n-1$ 个 $[2,x]$ 中不同的数,和为 $s$ 的方案数 $f[s],s\leq x$。先特判掉 $n=1$ 的情况(这是简单的,数组 $[r,r]$ 的 Complementary Sum 为 $\{r\}$)。
由此我们可以发现 $n$ 不能超过 $\mathcal{O}(\sqrt x)$,否则和一定超了。当然直接做背包还是做不了,因为你要记录当前的和,当前选了几个数,外面再套一层枚举 $[2,x]$ 显然时间复杂度爆了。这里我们可以考虑做类似 Lesbegue 积分的操作,记 $g[k]$ 表示 $e[2]\sim e[n]$ 中大于等于 $k$ 的数的个数,则有 $\displaystyle\sum_{k=1}^{\infty}g[k]=\sum_{i=2}^{n}e[i]$,原理见下图。
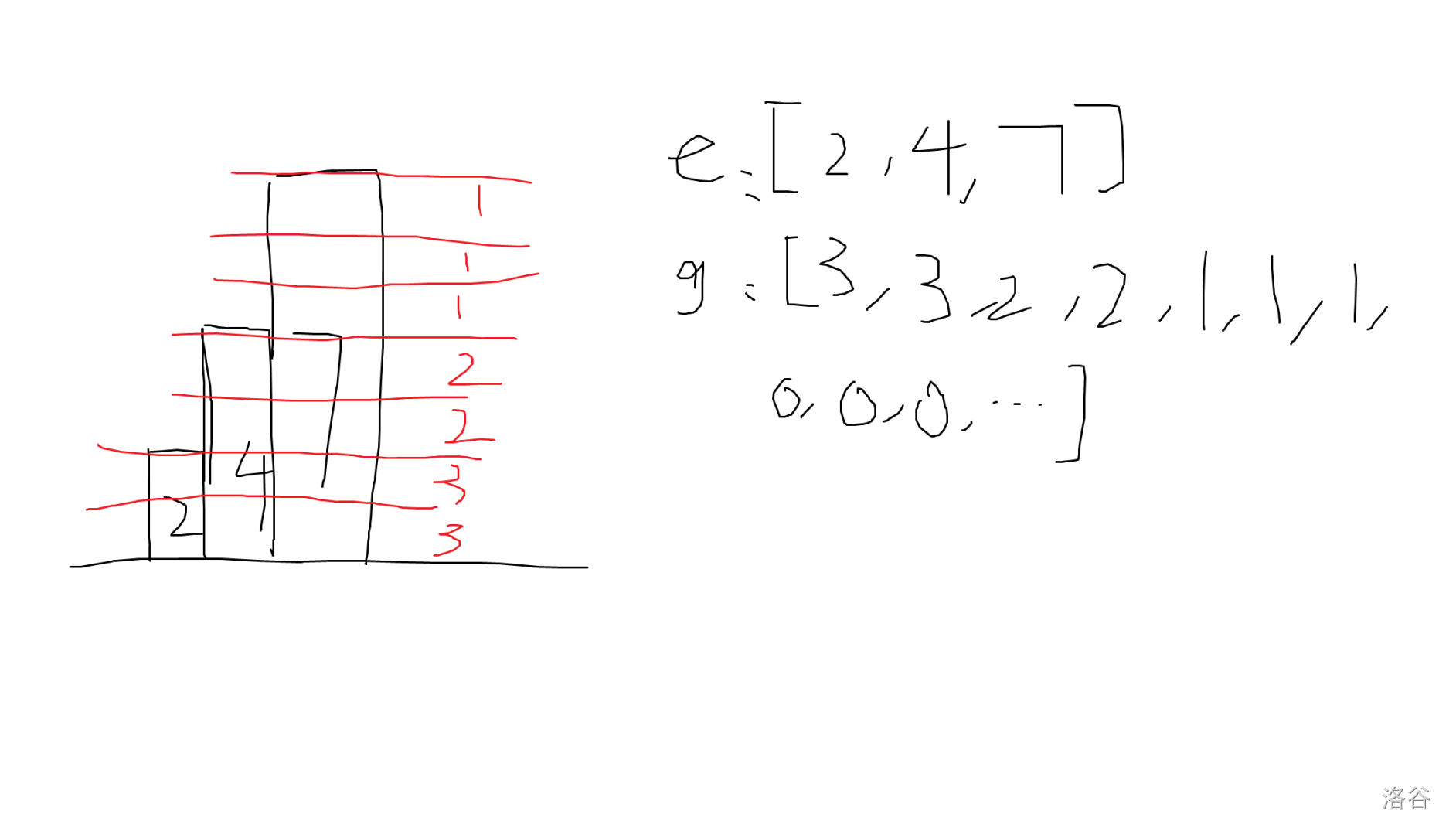
容易得到 $g[1]=g[2]=n-1$,且 $g[i]-g[i-1]\in \{0,-1\}$,这样子转化的好处是所有 $g[k]$ 中 $1\sim n-1$ 必然都出现了大于等于 $1$ 次,特别地,$n-1$ 必然出现了大于等于 $2$ 次,而不再有选数个数的限制。依次考虑 $1\sim n - 1$,每次加入一个新的 $i$,令 $f'[s]\leftarrow f[s-i]+f[s-2i]+\cdots$ 即可,实际上是一个完全背包。具体实现可以参考代码。
```cpp
#include <bits/stdc++.h>
const int mod = 998244353;
int mul(int x, int y){
return 1ll * x * y % mod;
}
int minus(int x, int y){
x -= y;
if(x < 0) x += mod;
return x;
}
int add(int x, int y){
x += y;
if(x >= mod) x -= mod;
return x;
}
int Qpow(int x, int y){
int r = 1;
while(y){
if(y & 1) r = mul(r, x);
x = mul(x, x); y >>= 1;
}
return r;
}
int n, x, f[200005], g[200005];
void solve(){
scanf("%d%d", &n, &x);
if(n == 1){
printf("%d\n", x);
return ;
}
int ans = 0;
if(1ll * (n + 2) * (n - 1) / 2 > x){
printf("0\n");
return ;
}
for(int i = 0; i <= x; ++i) f[i] = g[i] = 0;
f[0] = 1;
for(int i = 1; i <= n - 1; ++i){
for(int j = 0; j <= x; ++j){
if(j < i) g[j] = 0;
else g[j] = add(g[j - i], f[j - i]);
}
for(int j = x; j >= 0; --j){
f[j] = g[j];
if(i == n - 1 && j >= i) f[j] = minus(f[j], f[j - i]);
}
}
for(int j = 0; j <= x; ++j) ans = add(ans, mul(f[j], x - j + 1));
printf("%d\n", ans);
return ;
}
int main(){
int T = 1;
scanf("%d", &T);
while(T--) solve();
return 0;
}
```