[ABC315E]Prerequisites
CJ_Fu
·
·
题解
题目链接
洛谷
AtCoder
简要题意
给出 N 本书,可以阅读第 i 本书的前提是阅读第 P_{i,1}\sim P_{i,C_i} 本书,求阅读第一本书的最少书的本数,题目保证有解使得阅读完所有书籍。
输出任一阅读顺序(1 不需要输出)。
## 思路
很容易可以想到按照 $P_{i,j}\to i(1\le j\le C_i)$ 建边,比如样例 $1$:
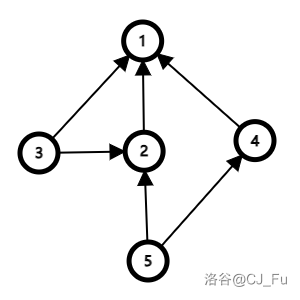
因为保证有解,所以在这个有向图上不存在环。
然后你发现事情没有这么简单,直接拓扑排序会有问题。因为这个有向图不一定连通(比如样例 $3$)。
所以我们可以先建原图的反图,然后以 $1$ 为根 DFS,搜到的点标记一下,然后再在原图中对应被标记的点上跑拓扑排序即可。
时间复杂度 $O(n)$。
## 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,c;
vector<int>e1[200003],e2[200003];
bool vis[200003]; // 标记
int in[200003],pro[200003],top;
#define pb emplace_back
void dfs(int u){
for(int v:e1[u]){
in[u]++;
e2[v].pb(u); // 原图
if(!vis[v]){
vis[v]=1;
dfs(v);
}
}
}
void Dfs(int u){
if(u!=1)cout<<u<<' ';
for(int v:e2[u])
if(!--in[v]) Dfs(v);
}
signed main(){
ios::sync_with_stdio(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>c;
for(int j=1,p;j<=c;j++){
cin>>p;
e1[i].pb(p); // 反图
}
}
vis[1]=1; dfs(1);
for(int i=1;i<=n;i++)
if(!in[i]&&vis[i]) pro[++top]=i;
for(int i=1;i<=top;i++) Dfs(pro[i]); // 拓扑
return 0;
}
```
可能是最近最水的 E 题?