P2221题解
jjsnam
·
·
题解
写在前面
最近期望学的头大。好久没有自己 AC 紫题了,碰巧这道题让我实现了。AC 后打开题解发现 1k 多人提交竟然还没有关闭题解通道?那赶紧来写一发。
前置知识
题目描述(戳这里查看原题)
正文
确定方向
对于求期望,我大致总结了 3 种方法:
- 期望 DP(一般是逆推)
- 根据期望定义推式子
- 由期望的线性性,通过结合概率和变量求解
那么对于这道题,第一种方法显然是不行的,只带 \log 的 DP 我做这么多题还没见过。因此我们更多从期望的定义以及其与概率的关系入手此题。
分析
根据此题中期望的定义,我们可以尝试求出所有情况的通行费用,并将每种情况乘以其对应的概率得到总期望。
又由于所有情况都是等概率,我们可以算出所有情况费用总和,乘以同一概率。写出来的式子写出来大概是:
E(l,r) = \dfrac 1 {P(l,r)} \times Sum_v
先来求 {P(l,r)}。询问区间 [l,r] 的长度 len = r-l+1。点 a 在区间中等概率选择,P(a) = \dfrac1 {len}。b 在剩下的 len - 1 个点中等概率选择,P(b) = \dfrac1 {len-1}。因而:
因此分母部分就是我们求出答案的**分母**。
------------
再来考虑分子,也就是所有情况的费用和。我们看一看样例的最后一次询问。询问 $[1,4]$。对应 $P(1,4) = \dfrac 1 {12}$。对应的分子,也就是所有情况的总费用,我们通过固定起点找终点,总和为 $34$(**注意正反向**)。因此答案 $E(1,4) = \dfrac {34} {12} = \dfrac {17} 6$。
如何求呢?在我们手动模拟时定起点找终点很麻烦,对于程序来说是 $O(n^2)$ 的,而且有许多不同的区间。我们不妨把问题拆解成**计算每一个相邻线段对答案的贡献**。
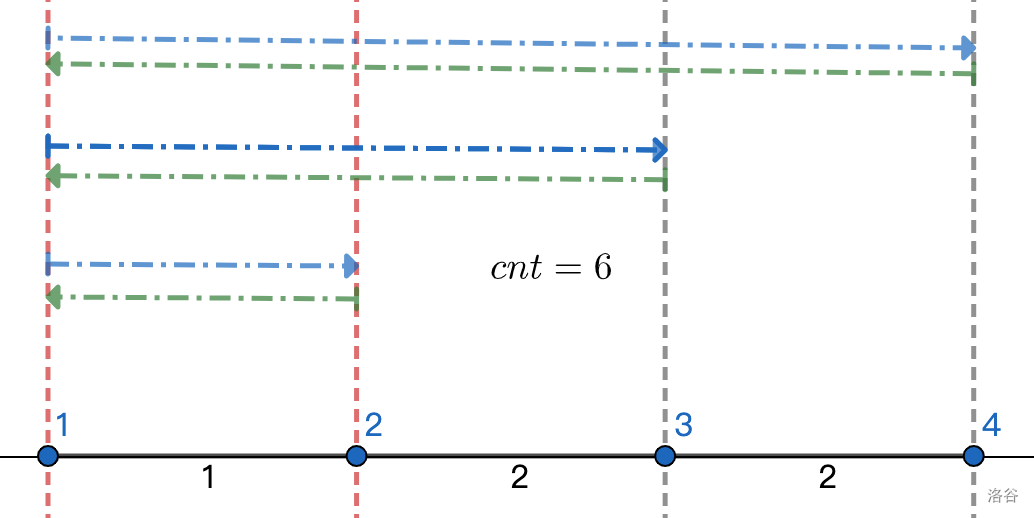
拿线段 $[1,2]$ 举例。起点为 1,路程覆盖 $3$ 次(蓝色),起点 2、3、4 分别覆盖 $1$ 次(绿色)。所以它对最后得分子贡献了 $6$ 次自己的费用。
继续思考。**在询问区间中**,线段 $[1,2]$ 左侧的端点只有 $1$ **这一个**,右侧总共有**三个点**。正向反向总共 $2\times(1\times 3) = 6$。似乎一条线段对最后总和的贡献只与它左右有多少起终点有关?细想确实合理。我们设线段左侧有 $p$ 个可能的起点,右侧有 $q$ 个可能的终点,根据乘法原理,包含该线段的路径总共有 $p\times q$ 个。考虑正反向再乘以 $2$。带入线段 $[2,3]$ 验证成功。($8=2\times(2 \times 2)$)
故对于询问区间 $[l,r]$ 的一条相邻线段 $[i,i+1]$,有:
$p = i-l+1$;$q = r-(i+1)+1 = r-i$。(就是区间长度)
所以我们的分子可以表示成每个相邻点线段贡献的次数乘以其费用(注意**右边界**):
$$ \displaystyle \sum_{i = l}^{r-1} {(i-l+1)\times(r-i)\times v_i} $$
## 实现
对于上述式子,以及数据范围,我们知道最好通过数据结构维护。又有区间加操作,我们考虑线段树。
然而,这个式子里都是乘法,怎么用线段树维护区间和呢?
我觉得大家刚学线段树的时候应该都做过类似维护高次和的线段树题,这题我们也可以这么尝试,毕竟对线段树的暗示已经很强烈了,如果不往下想想太可惜。
既然有乘法,我们就**拆乘法**。合并同次项看看能不能有什么新发现,有:
$$\begin{aligned}
&\displaystyle \sum_{i = l}^{r-1} {(i-l+1)\times(r-i)\times v_i} \\
&=\displaystyle \sum {(i\times r -i^2-l\times r+i\times l+r-i)\times v_i} \\
&=\displaystyle \sum {[(r-l\times r)+(l+r-1)\times i - i^2]\times v_i} \\
&=\displaystyle (r-l\times r)\times \sum_{i = l}^{r-1}{v_i} + (l+r-1)\times \sum_{i = l}^{r-1}{i\times v_i} - \sum_{i = l}^{r-1}{i^2\times v_i}
\end{aligned}
$$
这样我们成功将原式分离。对于 $v_i$、$i\times v_i$、$i^2\times v_i$,就可以考虑如何用线段树维护了。
具体的,我们将这三个和分别维护。对于区间 $[l,r]$ 增加 $v$ 的操作:
- **$v_i$**:对于一个节点 $now$ 所维护的和只需要增加区间长度乘以 $v$ 即可,即维护的值增加 $len_{now}\times v$。
- **$i\times v_i$**:这是就不是简单乘以区间长了。每个点实际增加的值是**不同的**,增加的值可表示为:$v\times \sum_{i=l}^{r}{i}$。因此我们要记录每个区间的 $\sum_{i=l}^{r}{i}$,这可以在建树时求出。
- **$i^2\times v_i$**:同理,请读者思考,最终我们在建树时要求得 $\sum_{i=l}^{r}{i^2}$。
这样我们就完全搞通这道题啦!
## 细节与注意
1. 线段树维护的是 $n-1$ 个线段,而不是 $n$ 个点,同样根据定义,在修改和查询时我们使用的区间是 $[l,r-1]$(根据输入的 $l$、$r$)。
2. 注意询问结果输出最简分数,对于求出的分子分母我们可以通过**欧几里得算法**计算公因子,然后同时除掉即可。
3. 考虑一下是否会爆 ```int```。乘积最大应当是 $(\dfrac n 2) ^2 = 2.5\times 10^9$,乘上最大贡献 $1\times 10^4$ 以及最大询问区间大概 $5\times 10^4$,则最后分子的数量级可至 $1\times 10^{18}$。同样分母也会爆。**需要 ```long long```**。(具体何处要开何处不要,请仔细思考,嫌麻烦直接 ```define int long long;``` 也是可以的)。
最终的时间复杂度是 $O(n\log n)$。
# 代码
变量名见注释。(其实这算是很好调的线段树了
```cpp
#include <iostream>
#include <algorithm>
#include <cstring>
#define ls (id << 1)
#define rs (id << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
typedef long long ll;//优雅一点不全用long long,就是调的久一点ಥ_ಥ
const int maxn = 100005;
struct SegmentTree{
ll sum0, sum1, sum2;
/* 根据乘i的次数命名。sum0就是v[i]*i^0=v[i], sum1就是v[i]*i,sum2就是v[i]*i^2 */
ll len, tot1, tot2;
/* len是区间长,tot1/2就是sum{i}和sum{i^2} */
ll lazy;//懒标记
}tr[maxn << 2];
int n, m;
struct Node{//线段树返回值
ll sum0, sum1, sum2;
Node operator + (const Node &b) const{//重载运算符方便返回
Node res;
res.sum0 = sum0 + b.sum0;
res.sum1 = sum1 + b.sum1;
res.sum2 = sum2 + b.sum2;
return res;
}
};
void pushup(int id){//通用 pushup
tr[id].sum0 = tr[ls].sum0 + tr[rs].sum0;
tr[id].sum1 = tr[ls].sum1 + tr[rs].sum1;
tr[id].sum2 = tr[ls].sum2 + tr[rs].sum2;
}
void build(int id, int l, int r){
tr[id].len = r - l + 1;
tr[id].lazy = 0;
if (l == r){
tr[id].sum0 = tr[id].sum1 = tr[id].sum2 = 0;
tr[id].tot1 = l, tr[id].tot2 = (ll)l * r;/* 注意爆int问题 */
return;
}
build(ls, l, mid), build(rs, mid+1, r);
pushup(id);
/* 额外 pushup 别忘了 */
tr[id].tot1 = tr[ls].tot1 + tr[rs].tot1;
tr[id].tot2 = tr[ls].tot2 + tr[rs].tot2;
}
void pushdown(int id){
if (tr[id].lazy){
ll temp = tr[id].lazy;
tr[id].lazy = 0;
tr[ls].lazy += temp, tr[rs].lazy += temp;
tr[ls].sum0 += tr[ls].len * temp,
tr[ls].sum1 += tr[ls].tot1 * temp,
tr[ls].sum2 += tr[ls].tot2 * temp;
tr[rs].sum0 += tr[rs].len * temp,
tr[rs].sum1 += tr[rs].tot1 * temp,
tr[rs].sum2 += tr[rs].tot2 * temp;
}
}
void update(int id, int l, int r, int a, int b, int v){
if (a <= l && r <= b){
tr[id].sum0 += tr[id].len * v,
tr[id].sum1 += tr[id].tot1 * v,
tr[id].sum2 += tr[id].tot2 * v;
tr[id].lazy += v;
return;
}
pushdown(id);
if (a <= mid) update(ls, l, mid, a, b, v);
if (b > mid) update(rs, mid+1, r, a, b, v);
pushup(id);
}
Node query(int id, int l, int r, int a, int b){
if (a <= l && r <= b){
return (Node){tr[id].sum0, tr[id].sum1, tr[id].sum2};
}
pushdown(id);
Node res = (Node){0, 0, 0};
if (a <= mid) res = res + query(ls, l, mid, a, b);
if (b > mid) res = res + query(rs, mid+1, r, a, b);
return res;
}
ll gcd(ll a, ll b){
return b ? gcd(b, a % b) : a;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
build(1, 1, n);
char op;
int l, r, v;
while (m --){
cin >> op;
if (op == 'C'){
cin >> l >> r >> v;
update(1, 1, n, l, r-1, v);
}
else{
cin >> l >> r;
ll N, D;//numerator分子, denominator分母
Node temp = query(1, 1, n, l, r-1);
N = (r - (ll)l * r) * temp.sum0 + (l + r - 1) * temp.sum1 - temp.sum2;
N <<= 1;
D = (ll)(r - l + 1) * (r - l);/* 再次注意爆int问题 */
ll d = gcd(N, D);
cout << N/d << '/' << D/d << endl;
}
}
return 0;
}
```
# 总结
主要是学习一下线段树和期望的结合。一定记住期望不只有 DP 一种实现方法。再遇到复杂式子不能直接上线段树时要勇于拆项合并同类项。瞪眼法没有用,只有勇于尝试多种方法,AC 才会到来。
感谢观看!