组合数学学习笔记
luuia
·
·
算法·理论
基础部分
一、加法原理
达成一个目标有 n 种不同的途径,而每条途径有 m_i 种不同的完成方式,那么达成这个目标的方式有 \sum_{i = 1}^nm_i 种。
二、乘法原理
达成一个目标有 n 个步骤,而每个步骤有 m_i 种不同的完成方式,那么达成这个目标的方式有 \prod_{i = 1}^nm_i 种。
三、排列与组合
容易得到 A_n^m = \dfrac{n!}{(n - m)!},C_n^m = \dfrac{n!}{(n - m)!m!}。
- 圆排列:从 n 个元素中选出 m 个围成一个圆的方案数,记作 Q_n^m。
如果我们不考虑圆,那么有 A_n^m 种。在排列成圆的情况下,每种循环位移会带来 m 种本质相同的排列,因此 Q_n^m = \dfrac{A_n^m}{m}。
记取出的 m 个数为 x_1,x_2,\cdots,x_m(x_1 \le x_2 \le \cdots \le x_n)。令 y_i = x_i + i - 1(1 \le i \le m),得到数列 y_1,y_2,\cdots,y_m,这些 y_i 是互不相同的,且 y_1 < y_2 < \cdots < y_m,因此它们可以看作从 (n+m-1) 个数中选出的 m 个数,即 H_n^m = C_{n+m-1}^m。
性质和定理
一、二项式定理
(a+b)^n = \sum_{i=0}^nC_n^ia^ib^{n-i}
上式右边 a 的幂次为 i,说明在左边的 n 个 (a+b) 中有 i 个选择了 a,因此系数为 C_n^i。
二、组合数的性质定理
二项式定理中,我们如果按照 b 来考虑,得到的系数应该是 C_n^{n-i},因此我们得到组合数的基础性质:
C_n^i = C_n^{n-i}
这是非常好理解的:在 n 个物品中选 i 个的方案数就等价于在 n 个物品中不选 (n-i) 个的方案数。
组合数的递推公式:
C_n^m = C_{n-1}^m+C_{n-1}^{m-1}
证明:
\begin{aligned}
C_{n-1}^m+C_{n-1}^{m-1} &= \frac{(n-1)!}{(n-m-1)!\,m!}+\frac{(n-1)!}{(n-m)!\,(m-1)!} \\
&= \frac{(n-1)!\,(n-m) + (n-1)!\,m}{m!\,(n-m)!}\\
&= \frac{n!}{m!\,(n-m)!}\\
&= C_n^m
\end{aligned}
组合数的其他性质:
-
-
C_n^k\times C_k^m = C_n^m \times C_{n-m}^{k-m} = C_n^{k-m} \times C_{n-k+m}^m
证明:
\begin{aligned}
C_n^k\times C_k^m &= \frac{n! \times k!}{k!\,m!\,(n-k)!\,(k-m)!}\\
&= \frac{n!}{\,m!\,(k-m)!\,(n-k)!}\\
C_n^m \times C_{n-m}^{k-m} &= \frac{n!\,(n-m)!}{m!\,(k-m)!\,(n-m)!\,(n-k)!}\\
&= \frac{n!}{m!\,(k-m)!\,(n-k)!}\\
C_n^{k-m} \times C_{n-k+m}^m &= \frac{n!\,(n-k+m)!}{m!\,(n-k+m)!\,(n-k)!\,(k-m)!} \\
&= \frac{n!}{m!\,(k-m)!\,(n-k)!}\\
\implies C_n^k\times C_k^m &= C_n^m \times C_{n-m}^{k-m} = C_n^{k-m} \times C_{n-k+m}^m
\end{aligned}
-
C_{n+m+1}^m = \sum_{i=0}^mC_{n+i}^i
证明:
\begin{aligned}
\sum_{i=0}^mC_{n+i}^i &= C_n^0 + C_{n+1}^1 + C_{n+2}^2 \cdots + C_{n+m}^m \\
&= C_{n+1}^0 + C_{n+1}^1 + C_{n+2}^2\cdots + C_{n+m}^m \\
&= C_{n+2}^1 + C_{n+2}^2 \cdots + C_{n+m}^m \\
&= C_{n+m}^{m-1}+ C_{n+m}^m \\
&=C_{n+m+1}^m
\end{aligned}
组合数的求法:
-
根据递推式预处理,时间 O(nm + q),空间 O(nm)。
-
预处理阶乘,求出 m! 和 (n-m)! 模 p 意义下的逆元直接算即可,要求 p 是质数,否则可能没有逆元,时间 O(n+q\log p),空间 O(n)。
-
预处理阶乘和阶乘的逆元,直接套公式算,同样要求 p 是质数,时间 O(n+q),空间 O(n)。
-
使用卢卡斯定理计算,预处理阶乘和阶乘的逆元至 p,适用于 n 较大 (n \ge 10^{9}),p 较小 (p \le 10^5) 时,时间 O(p+q \log n),空间 O(p)。
三、卢卡斯定理
Lucas 定理用于求解大组合数取模的问题,其中模数必须为素数。正常的组合数运算可以通过递推公式求解但当问题规模很大,而模数是一个不大的质数的时候,就不能简单地通过递推求解来得到答案,需要用到 Lucas 定理。
Lucas 定理内容如下:对于质数 p,有
C_n^m\bmod p = C_{\lfloor n/p\rfloor} ^ {\lfloor m/p\rfloor}\cdot C_{n \bmod p}^{m \bmod p}\bmod p
观察上述表达式,可知 n\bmod p 和 m\bmod p 一定是小于 p 的数,可以直接求解,
边界条件:当 $m=0$ 的时候,返回 $1$。
时间复杂度为 $O(\log n)$,默认计算组合数复杂度为 $O(1)$,具体预处理阶乘和阶乘逆元至 $p$ 即可。
代码实现:
```cpp
long long Lucas(long long n, long long m, long long p)
{
if (m == 0) return 1;
return (C(n % p, m % p, p) * Lucas(n / p, m / p, p)) % p;
}
```
### 范德蒙德卷积
---
$$\sum_{i=0}^kC_{n}^{i}C_{m}^{k-i}=C_{n+m}^{k}$$
证明:
$$
\begin{aligned}
&\,\,\,\,\,\,\,\sum_{k=0}^{n+m}C_{n+m}^{k}x^k\\
&=(x+1)^n(x+1)^m\\
&=\sum_{r=0}^nC_{n}^{r}x^r\sum_{s=0}^mC_{m}^{s}x^s\\
&=\sum_{k=0}^{n+m}\sum_{r=0}^kC_{n}^{r}C_{m}^{k-r}x^k\\
\implies &C_{n+m}^{k}=\sum_{r=0}^kC_{n}^{r}C_{m}^{k-r}
\end{aligned}
$$
### 抽屉原理与容斥原理
---
#### 一、抽屉原理
将 $n$ 个物体,划分为 $k$ 组,那么至少存在一个分组,含有大于或等于 $\lceil\dfrac{n}{k}\rceil$ 个物品。
证明:若每个组的物品数量都小于 $\lceil\dfrac{n}{k}\rceil$,那么物体的总数 $n < (\lceil\dfrac{n}{k}\rceil-1) \times k < (\dfrac{n}{k}+1-1) \times k=n$,矛盾,故原命题得证。
#### 二、容斥原理
设全集 $U$ 中元素有 $n$ 种不同的属性,而第 $i$ 种属性 $P_i$,拥有属性 $P_i$ 的元素构成集合 $S_i$,那么
$$
\begin{aligned}
\left|\bigcup_{i=1}^{n}S_i\right|=&\sum_{i}|S_i|-\sum_{i<j}|S_i\cap S_j|+\sum_{i<j<k}|S_i\cap S_j\cap S_k|-\cdots\\
&+(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^{m}S_{a_i}\right|+\cdots+(-1)^{n-1}|S_1\cap\cdots\cap S_n|
\end{aligned}
$$
### 卡特兰数
---
卡特兰数(Catalan Number)是组合数学的计数问题中较为常见的一个数列。
#### 一、公式
卡特兰数的第 $n$ 项 $H_n$ 的含义为:在平面直角坐标系中,从 $(0,0)$ 出发,每次只能向上走或者向右走,且不能越过 $y = x$ 这条直线(可以碰到),求走到 $(n,n)$ 的不同路径的数量。
- 不能越过 $y=x$,相当于不能碰到 $y=x+1$。
下图中的红色路径就是一条不合法的路径。
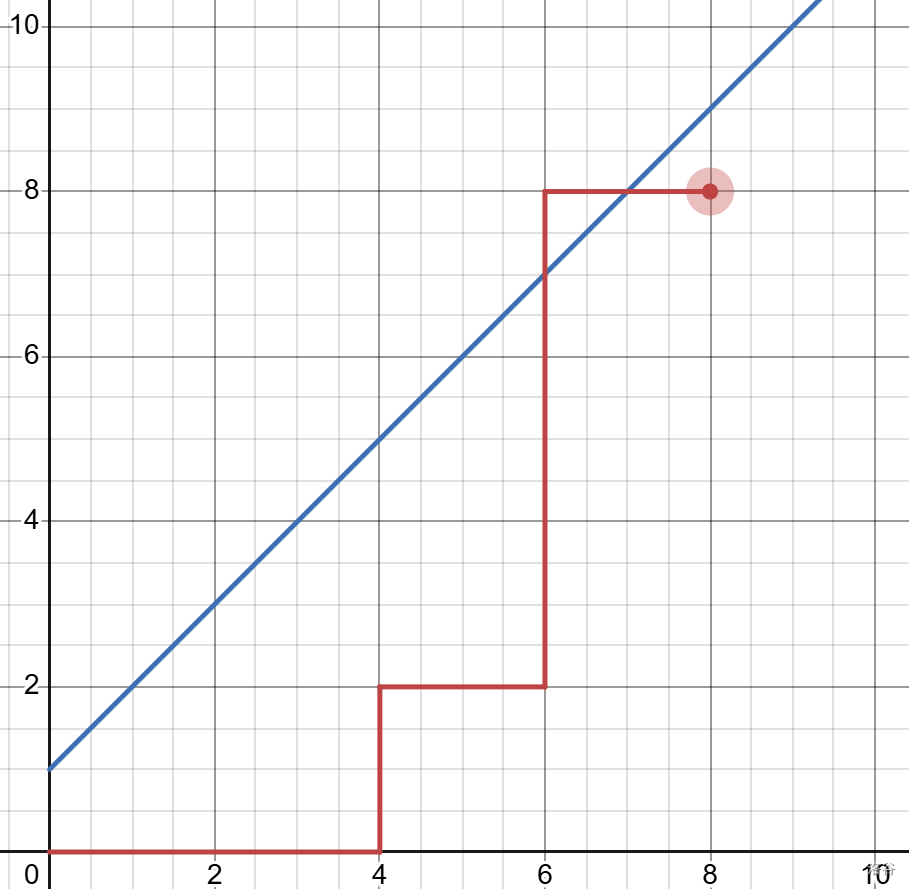
我们设其路径上第一个碰到的 $y=x+1$ 的交点是 $(t,t+1)$,将 $(t,t+1) \to (n,n)$ 的路径沿着 $y=x+1$ 对称,就得到了绿色路径,它的终点变为了 $(n-1,n+1)$。
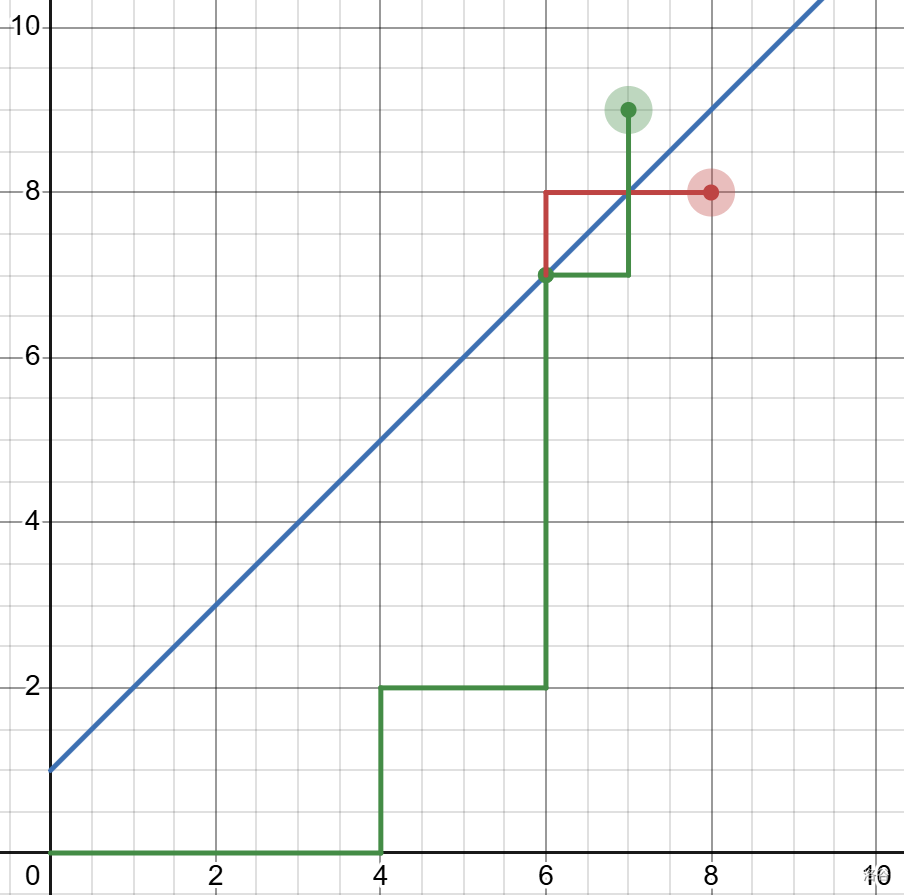
由此得知,每一条不合法的路径最终都能映射到一条由 $(0,0)$ 到 $(n-1,n+1)$ 的路径,方案数为 $C_{2n}^{n-1}$,而路径总数有 $C_{2n}^n$ 条,因此合法方案即 $H_n$ 有:
$$
\begin{aligned}
H_n &= C_{2n}^n-C_{2n}^{n-1} \\
&= \frac{(2n)!}{(n!)^2} - \frac{(2n)!}{(n-1)!\,(n+1)!} \\
&= \frac{(2n)!}{n!\,(n+1)!} \\
&= \frac{C_{2n}^n}{n+1} \\
\implies H_n &= C_{2n}^n-C_{2n}^{n-1} = \frac{C_{2n}^n}{n+1}
\end{aligned}
$$
卡特兰数还有递推公式:
- $$H_n = \sum_{i=0}^{n-1}H_iH_{n-i-1}$$
- $$H_n = \frac{4n-2}{n+1}H_{n-1}$$
证明:$(0,0)$ 到 $(n,n)$ 的路径可以分作以下几步:
- 从 $(0,0)$ 走到 $(i,i)$,方案数为 $H_i$。
- 从 $(i,i)$ 走到 $(n-1,n-1)$,方案数为 $H_{n-i-1}$。
- 从 $(n-1,n-1)$ 走到 $(n,n)$,方案数为 $1$。
枚举每一个 $i$,由此得到 $H_n = \sum_{i=0}^{n-1}H_iH_{n-i-1}$。
$$
\begin{aligned}
& H_n = \frac{4n-2}{n+1}H_{n-1} \\
\iff & \frac{C_{2n}^n}{n+1} = \frac{4n-2}{n+1} \times \frac{C_{2n-2}^{n-1}}{n} \\
\iff & \frac{(2n)!}{(n+1)(n!)^2} = \frac{4n-2}{n+1} \times \frac{(2n-2)!}{n(n-1)!^2} \\
\iff & \frac{(2n)!}{n} = (4n-2) \times {(2n-2)!} \\
\iff & \frac{(2n)(2n-1)}{n} = 4n-2 \\
\iff & 4n-2 = 4n-2 \\
\end{aligned}
$$
故得证。
#### 二、应用
卡特兰数的常见模型如下:
1. 由 $n$ 对左右括号构成的合法的括号序列数
括号序列问题中,要求任何一个前缀,其左括号的数量不少于右括号的数量,我们把坐标系问题的“向右走”和“向上走”映射为一个操作序列,将“向右走”映射为“左括号”,将“向上走”映射为“右括号”。
我们可以发现两个问题是双射的,也就是一个合法的括号序列,总是能对应上述问题中坐标系中的一条合法路径,因此答案为 $H_n$。
2. 一个栈的进栈顺序为 $1,2,\cdots,n$,求它有多少个不同的出栈顺序?
记进栈为 $+1$,出栈为 $-1$,那么因为每一个元素出栈时栈不能为空,因此每一个前缀和都必须不小于 $0$,我们把入栈操作想象为左括号,出栈操作想象为右括号,那么对栈的操作就变成了一个括号序列,因此答案仍然为 $H_n$。
3. $n$ 个节点可以构造出多少个不同的二叉树?
假设现在仅有一个根节点,我们需要构造这棵树,添加上其余的 $n-1$ 个节点。一棵树为二叉树,则它的左右子树要么为空,要么也为二叉树,若根节点的左子树有 $i$ 个节点,则构造左子树的方案数有 $H_i$ 种,右子树有 $n-i-1$ 个节点,构造右子树的方案数为 $H_{n-i-1}$,因此有 $H_n = \sum_{i=0}^{n-1}H_iH_{n-i-1}$,同样为卡特兰数。
4. 对角线不相交的情况下,将一个正凸多边形区域分成三角形区域的方法数?
因为多边形的某条边,最后一定对应于某个切割出来的三角形,我们将这个三角形取出:选取一条边,再选择一个顶点(不在这条边上的),构成该三角形。然后多边形就被分为了左右两个部分,即凸 $i$ 边形,和凸 $n-i+2$ 边形,然后对左右两边再单独划分三角形即可,因此方案数为 $H_{n-2}$。
5. $n$ 个 $+1$ 和 $n$ 个 $-1$ 构成长度为 $2n$ 的序列,求使得每一个前缀和都不小于 $0$ 的序列个数。
我们把坐标系问题的“向右走”和“向上走”映射为一个序列,将“向右走”映射为 $+1$,将“向上走”映射 $-1$。我们可以发现两个问题是双射的,也就是一个合法的序列,总是能对应上述问题中坐标系中的一条合法路径,因此答案为 $H_n$。
6. 在圆上选择 $2n$ 个点,将这些点成对连接起来使得所得到的 $n$ 条线段不相交的方法数?
想象为选点不好理解,我们想象为选线段,或者用刀来切
第一刀随便切,接下来还剩下 $n-1$ 刀,我要分配给左边 $i$ 刀,右边 $n-i-1$ 刀,方案数为 $\sum_{i=0}^{n-1}H_iH_{n-i-1}$,即为 $H_n$。
7. 有 $2n$ 个人排成一行进入剧场,入场费 $5$ 元。其中只有 $n$ 个人有一张 $5$ 元钞票,另外 $n$ 人只有 $10$ 元钞票,剧院无其它钞票,问有多少种方法使得只要有 $10$ 元的人买票,售票处就有 $5$ 元的钞票找零?
要求每个人买完票都有钱找零,则需要在任意时候用 $5$ 元钞票买票的人都不小于用 $10$ 元钞票买票的人,则记用 $5$ 元的人为 $+1$,用 $10$ 元的人为 $-1$,则要求序列的每一个前缀和都不小于 $0$,答案为卡特兰数 $H_n$。
### 斯特林数
---
#### 一、自然幂,上升幂和下降幂、二项式反演
自然幂:$m^n$ 称作 $m$ 的 $n$ 次方,公式表达如下:
$$m^n = \prod_{i=0}^{n-1}m$$
上升幂:记作 $m^{\overline{n}}$,公式表达如下:
$$m^{\overline{n}} = \prod_{i=0}^{n-1}(m+i)$$
下降幂:记作 $m^{\underline{n}}$,公式表达如下:
$$m^{\underline{n}} = \prod_{i=0}^{n-1}(m-i)$$
上升幂和下降幂的转换:
$$(-m)^{\overline{n}} = (-1)^nm^{\underline{n}}$$
$$(-m)^{\underline{n}} = (-1)^nm^{\overline{n}}$$
二项式反演:
$$f(n)=\sum_{i=0}^nC_n^ig(i)\iff g(n)=\sum_{i=0}^nC_n^i(-1)^{n-i}f(i)$$
证明:
$$
\begin{aligned}
\sum_{i=0}^nC_n^i(-1)^{n-i}f(i)&=\sum_{i=0}^nC_n^i(-1)^{n-i}\sum_{j=0}^iC_i^jg(j)\\
&=\sum_{i=0}^n\sum_{j=0}^iC_n^iC_i^j(-1)^{n-i}g(j)\\
&=\sum_{i=0}^n\sum_{j=0}^iC_n^jC_{n-j}^{i-j}(-1)^{n-i}g(j)\\
&=\sum_{j=0}^nC_n^jg(j)\sum_{i=j}^nC_{n-j}^{i-j}(-1)^{n-i}\\
&=\sum_{j=0}^nC_n^jg(j)\sum_{i=0}^{n-j}C_{n-j}^{i}(-1)^{n-j-i}\\
&=\sum_{j=0}^nC_n^jg(j)\cdot 0^{n-j}\\
&=g(n)\\
\end{aligned}
$$
#### 二、第一类斯特林数
第一类斯特林数 $\begin{bmatrix}n\\m\end{bmatrix}$,表示将 $n$ 个两两不同的元素,划分成 $m$ 个圆排列的方案数。
第一类斯特林数的递推式:
$$\begin{aligned}\begin{bmatrix} n \\ m \end{bmatrix}=\begin{bmatrix} n-1 \\ m-1 \end{bmatrix} +(n-1) \begin{bmatrix} n-1 \\ m \end{bmatrix}\end{aligned}$$
递推边界为 $\begin{bmatrix}n\\0\end{bmatrix}=[n=0]$,证明:
- 将新加入的一个元素独立作为一个圆排列,方案数为 $\begin{bmatrix}n-1\\m-1\end{bmatrix}$。
- 新加入的元素加入现有的圆排列当中,不妨设有 $q$ 个圆排列,第 $i$ 个圆排列长度为 $l_i$,对任意长度为 $l$ 的圆排列插入元素的方案数为 $l$,根据加法原理,共有 $\sum_{i=1}^q l_i = n-1$ 种插入方式,因此方案数为 $(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}$。
根据加法原理,将两式相加即可得到递推式。
第一类斯特林数的性质:
1. $$\sum_{i=0}^n \begin{bmatrix}n\\i\end{bmatrix} = n!$$
证明:
考虑数学归纳法:当 $n=0$ 时,等式显然成立。
不妨设 $n=k$ 时式子成立,当 $n=k+1$ 时,
$$
\begin{aligned}
& \,\,\,\,\,\,\,\sum_{i=0}^{k+1} \begin{bmatrix}k+1\\i\end{bmatrix}\\
&= \sum_{i=1}^{k+1} \begin{bmatrix}k\\i-1\end{bmatrix} + \sum_{i=0}^{k+1}k \times \begin{bmatrix}k\\i\end{bmatrix}\\
&= \sum_{i=0}^k \begin{bmatrix}k\\i\end{bmatrix} + k \times \sum_{i=0}^{k+1} \begin{bmatrix}k\\i\end{bmatrix}\\
&= \sum_{i=0}^k \begin{bmatrix}k\\i\end{bmatrix} + k \times \sum_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix} + \begin{bmatrix}k\\k+1\end{bmatrix}\\
&= \sum_{i=0}^k \begin{bmatrix}k\\i\end{bmatrix} + k \times \sum_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix} \,\,\,\,\,\,\,(\begin{bmatrix}k\\k+1\end{bmatrix}=0)\\
&= k! + k \times k! \\ &= (k+1)!
\end{aligned}
$$
根据数学归纳法,原式得证。
2. $$\sum_{i=0}^n \begin{bmatrix}n\\i\end{bmatrix}m^i = m^{\overline{n}}$$
证明:
考虑数学归纳法:当 $n=0$ 时,等式显然成立。
不妨设 $n=k$ 时式子成立,当 $n=k+1$ 时,
$$
\begin{aligned}
& \,\,\,\,\,\,\,\sum_{i=0}^{k+1}\begin{bmatrix}k+1\\i\end{bmatrix}m^i\\
&= \sum_{i=0}^{k+1}\begin{bmatrix}k\\i-1\end{bmatrix}m^i +\sum_{i=0}^{k+1}k \times \begin{bmatrix}k\\i\end{bmatrix}m^i \\
&= \sum_{i=1}^{k+1}\begin{bmatrix}k\\i-1\end{bmatrix}m^i +k \times\sum_{i=0}^{k+1} \begin{bmatrix}k\\i\end{bmatrix}m^i \\
&= \sum_{i=0}^{k}\begin{bmatrix}k\\i\end{bmatrix}m^{i+1} +k \times\sum_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix}m^i \,\,\,\,\,\,\,(\begin{bmatrix}k\\k+1\end{bmatrix}=0)\\
&= m \times\sum_{i=0}^{k}\begin{bmatrix}k\\i\end{bmatrix}m^{i} +k \times\sum_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix}m^i \\
&= (m+k) \times\sum_{i=0}^{k}\begin{bmatrix}k\\i\end{bmatrix}m^{i} \\
&= (m+k)\,m^{\overline{k}}\\
&= m^{\overline{k+1}}
\end{aligned}
$$
根据数学归纳法,原式得证。
3. $$\sum_{i=0}^n (-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}m^i = m^{\underline{n}}$$
证明:
$$
\begin{aligned}
& \,\,\,\,\,\,\,\sum_{i=0}^n (-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}m^i\\
&=(-1)^n\sum_{i=0}^n (-1)^i\begin{bmatrix}n\\i\end{bmatrix}m^i\\
&=(-1)^n\sum_{i=0}^n\begin{bmatrix}n\\i\end{bmatrix}(-m)^i\\
&=(-1)^n(-m)^{\overline{n}}\\
&=(-1)^n(-1)^n m^{\underline{n}}\\
&=m^{\underline{n}}\\
\end{aligned}
$$
得证。
---
同一行第一类斯特林数的计算:[P5408 第一类斯特林数·行](https://www.luogu.com.cn/problem/P5408)
构造生成函数 $F(x)^n = \prod_{i=0}^{n-1}(x+i) = \prod_{i=0}^na_ix^i$,根据前面的性质二得到其中的 $a_i = \begin{bmatrix} n \\ i \end{bmatrix}$。
显然 $F(x)^{2n} = F(x)^n F(x + n)^n$,于是考虑倍增。
$$
\begin{aligned}
F(x+n)^n &= \sum_{i=0}^na_i(x+n)^i \\
&= \sum_{i=0}^na_i\sum_{j = 0}^iC_i^jx^jn^{i-j} \\
&= \sum_{i=0}^n\sum_{j=i}^nC_j^ix^in^{j-i}a_j\\
&= \sum_{i=0}^n\sum_{j=i}^n\frac{j!}{i!(j-i)!}x^in^{j-i}a_j\\
&= \sum_{i=0}^n\frac{1}{i!}(\sum_{j=i}^na_jj!\frac{n^{j-i}}{(j-i)!}x^i)\\
\end{aligned}
$$
我们可以通过左半部分系数得到右半部分系数由此得到全部的系数。
时间复杂度:$T(n) = T(\frac{n}{2}) + O(n \log n) = O(n\log n)$。
```cpp
#include <bits/stdc++.h>
using namespace std;
long long read()
{
long long s = 0,w = 1;
char ch = getchar();
while(ch < '0' || ch > '9')
{
if(ch == '-') w = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9')
{
s =(s << 1) +(s << 3) +(ch ^ 48);
ch = getchar();
}
return s * w;
}
void write(long long a)
{
if(a > 9) write(a / 10);
putchar(a % 10 + '0');
}
const int N = 1e6 + 10,p = 167772161,inv3 = 55924054;
long long n,len,limit,rk[N],a[N],b[N],fac[N],ifac[N],answer[N];
long long quickpow(long long c,long long n,long long m)
{
long long res = 1;
while(n)
{
if(n & 1) res = res * c % m;
c = c * c % m;
n >>= 1;
}
return res;
}
void init_fac(long long m)
{
fac[0] = ifac[0] = 1;
for(int i = 1;i <= m;i++) fac[i] = fac[i - 1] * i % p;
ifac[m] = quickpow(fac[m],p - 2,p);
for(int i = m;i >= 1;i--) ifac[i - 1] = ifac[i] * i % p;
}
void init(long long m)
{
len = 0,limit = 1;
while(limit <= m){limit <<= 1,++len;}
for(int i = 0;i < limit;i++) rk[i] = (rk[i >> 1] >> 1) | ((i & 1) << (len - 1));
}
void NTT(long long x[])
{
for(int i = 0;i < limit;i++) if(i < rk[i]) swap(x[i],x[rk[i]]);
for(int mid = 1;mid < limit;mid <<= 1)
{
long long gn = quickpow(3,(p - 1) / (mid << 1),p);
for(int j = 0;j < limit;j += mid << 1)
{
long long g = 1;
for(int i = 0;i < mid;i++,(g *= gn) %= p)
{
long long tmp1 = x[i + j],tmp2 = x[i + j + mid] * g % p;
x[i + j] = (tmp1 + tmp2) % p;
x[i + j + mid] = (tmp1 - tmp2) % p;
}
}
}
}
void INTT(long long x[])
{
for(int i = 0;i < limit;i++) if(i < rk[i]) swap(x[i],x[rk[i]]);
for(int mid = 1;mid < limit;mid <<= 1)
{
long long gn = quickpow(inv3,(p - 1) / (mid << 1),p);
for(int j = 0;j < limit;j += mid << 1)
{
long long g = 1;
for(int i = 0;i < mid;i++,(g *= gn) %= p)
{
long long tmp1 = x[i + j],tmp2 = x[i + j + mid] * g % p;
x[i + j] = (tmp1 + tmp2) % p;
x[i + j + mid] = (tmp1 - tmp2) % p;
}
}
}
long long inv = quickpow(limit,p - 2,p);
for(int i = 0;i < limit;i++) x[i] *= inv,x[i] %= p;
}
void solve(long long n)
{
if(n == 1){answer[1] = 1;return;}
long long last = n / 2;solve(last);
for(int i = 0;i <= last;i++) a[last - i] = answer[i] * fac[i] % p;
long long power = 1;
for(int i = 0;i <= last;i++,(power *= last) %= p) b[i] = power * ifac[i] % p;
init(last * 2),NTT(a),NTT(b);
for(int i = 0;i < limit;i++) a[i] *= b[i],a[i] %= p;
INTT(a),reverse(a,a + last + 1);
for(int i = 0;i <= last;i++) a[i] *= ifac[i],a[i] %= p;
fill(a + last + 1,a + limit,0),fill(b,b + limit,0);
init(n),NTT(answer),NTT(a);
for(int i = 0;i < limit;i++) answer[i] *= a[i],answer[i] %= p;
INTT(answer),fill(a,a + limit,0);
if(n & 1){for(int i = n;i >= 1;i--) answer[i] = (answer[i - 1] + (n - 1) * answer[i]) % p;}
}
int main()
{
// freopen("input.in","r",stdin);
n = read(),init_fac(n);
if(n == 0){cout << 1 << endl;return 0;}solve(n);
for(int i = 0;i <= n;i++) cout << (answer[i] % p + p) % p << ' ';
cout << endl;return 0;
}
```
同一列第一类斯特林数的计算:[P5409 第一类斯特林数·列](https://www.luogu.com.cn/problem/P5409)
#### 三、第二类斯特林数
第二类斯特林数 $\begin{Bmatrix}n\\m\end{Bmatrix}$,表示将 $n$ 个两两不同的元素,划分成 $m$ 个互不区分的非空子集的方案数。
第二类斯特林数的递推式:
$$\begin{aligned}\begin{Bmatrix} n \\ m \end{Bmatrix}=\begin{Bmatrix} n-1 \\ m-1 \end{Bmatrix} +m \begin{Bmatrix} n-1 \\ m \end{Bmatrix}\end{aligned}$$
递推边界为 $\begin{Bmatrix}n\\0\end{Bmatrix}=[n=0]$,证明:
- 将新加入的一个元素独立作为一个子集,方案数为 $\begin{Bmatrix}n-1\\m-1\end{Bmatrix}$。
- 新加入的元素加入现有的 $m$ 个非空子集当中,方案数为 $m\begin{Bmatrix}n-1\\m\end{Bmatrix}$。
根据加法原理,将两式相加即可得到递推式。
第二类斯特林数的性质:
1. $$\sum ^{n}_{i=0}\begin{Bmatrix} n \\ i \end{Bmatrix}m^{\underline{i}}=m^{n}$$
证明:
考虑数学归纳法:当 $n=0$ 时,等式显然成立。
不妨设 $n=k$ 时式子成立,当 $n=k+1$ 时,
$$
\begin{aligned}
& \,\,\,\,\,\,\,\sum_{i=0} ^{k+1}\begin{Bmatrix} k+1 \\ i \end{Bmatrix}m^{\underline{i}}\\
&= \sum_{i=0} ^{k+1}\begin{Bmatrix} k \\ i-1 \end{Bmatrix}m^{\underline{i}}+\sum _ {i=0}^{k+1}i\begin{Bmatrix} k \\ i \end{Bmatrix}m^{\underline{i}} \\
&= \sum_{i=0} ^{k}\begin{Bmatrix} k \\ i \end{Bmatrix}m^{\underline{i+1}}+\sum _ {i=0}^{k}i\begin{Bmatrix} k \\ i \end{Bmatrix}m^{\underline{i}} \\
&= \sum_{i=0} ^{k}(m-i)\begin{Bmatrix} k \\ i \end{Bmatrix}m^{\underline{i}}+\sum _ {i=0}^{k}i\begin{Bmatrix} k \\ i \end{Bmatrix}m^{\underline{i}} \\
&= m\sum_{i=0} ^{k}\begin{Bmatrix} k \\ i \end{Bmatrix}m^{\underline{i}}\\
&=m \times m^k\\&=m^{k+1}
\end{aligned}
$$
根据数学归纳法,原式得证。
2. $$\sum ^{n}_{i=0}(-1)^{n-i}\begin{Bmatrix} n \\ i \end{Bmatrix}m^{\overline{i}}=m^{n}$$
证明:
$$
\begin{aligned}
& \,\,\,\,\,\,\,\sum ^{n}_{i=0}(-1)^{n-i}\begin{Bmatrix} n \\ i \end{Bmatrix}m^{\overline{i}}\\
&= (-1)^n\sum _ {i=0}^{n}\begin{Bmatrix} n \\ i \end{Bmatrix}(-1)^im^{\overline{i}}\\
&= (-1)^n\sum _{i=0}^{n}\begin{Bmatrix} n \\ i \end{Bmatrix}(-m)^{\underline{i}}\\
&= (-1)^n(-m)^n\\&=m^n
\end{aligned}
$$
得证。
第二类斯特林数的通项公式:
$$\begin{Bmatrix} n \\ m \end{Bmatrix} = \sum_{i = 0}^m\frac{(-1)^{m-i}i^n}{i!(m-i)!}$$
证明:
考虑二项式反演。
令 $f_i$ 为表示将 $n$ 个两两不同的元素,划分为 $i$ 个互不相同的**非空子集**的方案数。
令 $g_i$ 为表示将 $n$ 个两两不同的元素,划分为 $i$ 个互不相同的**子集**的方案数。
显然 $f_i = i!\begin{Bmatrix} n \\ i \end{Bmatrix}$,$g_i = n^i$。
我们考虑 $f_i$ 其实就是 $g_i$ 去掉所有的空子集,则我们只要钦定 $g_i$ 中那些是非空子集就可以写出 $f_i$ 和 $g_i$ 的关系了:
$$g_i = \sum_{j=0}^iC_i^jf_j$$
根据二项式反演:
$$
\begin{aligned}
f_i &= \sum_{j=0}^i(-1)^{i-j}C_i^jg_j \\
&= \sum_{j=0}^i(-1)^{i-j}C_i^jj^n \\
&= \sum_{j=0}^i\frac{(-1)^{i-j}i!\,j^n}{j!(i-j)!} \\
\end{aligned}
$$
因此,我们得到:
$$\begin{Bmatrix} n \\ m \end{Bmatrix} = \frac{f_m}{m!} = \sum_{i = 0}^m\frac{(-1)^{m-i}i^n}{i!(m-i)!}$$
同一行第二类斯特林数的计算:[P5395 第二类斯特林数·行](https://www.luogu.com.cn/problem/P5395)
根据通项公式,可以发现这是卷积的形式,直接卷积计算即可。
```cpp
#include <bits/stdc++.h>
using namespace std;
long long read()
{
long long s = 0,w = 1;
char ch = getchar();
while(ch < '0' || ch > '9')
{
if(ch == '-') w = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9')
{
s =(s << 1) +(s << 3) +(ch ^ 48);
ch = getchar();
}
return s * w;
}
void write(long long a)
{
if(a > 9) write(a / 10);
putchar(a % 10 + '0');
}
const int N = 1e6 + 10,p = 167772161,inv3 = 55924054;
long long n,len,limit,rk[N],a[N],b[N],fac[N],ifac[N],answer[N];
long long quickpow(long long c,long long n,long long m)
{
long long res = 1;
while(n)
{
if(n & 1) res = res * c % m;
c = c * c % m;
n >>= 1;
}
return res;
}
void init_fac(long long m)
{
fac[0] = ifac[0] = 1;
for(int i = 1;i <= m;i++) fac[i] = fac[i - 1] * i % p;
ifac[m] = quickpow(fac[m],p - 2,p);
for(int i = m;i >= 1;i--) ifac[i - 1] = ifac[i] * i % p;
}
void init(long long m)
{
len = 0,limit = 1;
while(limit <= m){limit <<= 1,++len;}
for(int i = 0;i < limit;i++) rk[i] = (rk[i >> 1] >> 1) | ((i & 1) << (len - 1));
}
void NTT(long long x[])
{
for(int i = 0;i < limit;i++) if(i < rk[i]) swap(x[i],x[rk[i]]);
for(int mid = 1;mid < limit;mid <<= 1)
{
long long gn = quickpow(3,(p - 1) / (mid << 1),p);
for(int j = 0;j < limit;j += mid << 1)
{
long long g = 1;
for(int i = 0;i < mid;i++,(g *= gn) %= p)
{
long long tmp1 = x[i + j],tmp2 = x[i + j + mid] * g % p;
x[i + j] = (tmp1 + tmp2) % p;
x[i + j + mid] = (tmp1 - tmp2) % p;
}
}
}
}
void INTT(long long x[])
{
for(int i = 0;i < limit;i++) if(i < rk[i]) swap(x[i],x[rk[i]]);
for(int mid = 1;mid < limit;mid <<= 1)
{
long long gn = quickpow(inv3,(p - 1) / (mid << 1),p);
for(int j = 0;j < limit;j += mid << 1)
{
long long g = 1;
for(int i = 0;i < mid;i++,(g *= gn) %= p)
{
long long tmp1 = x[i + j],tmp2 = x[i + j + mid] * g % p;
x[i + j] = (tmp1 + tmp2) % p;
x[i + j + mid] = (tmp1 - tmp2) % p;
}
}
}
long long inv = quickpow(limit,p - 2,p);
for(int i = 0;i < limit;i++) x[i] *= inv,x[i] %= p;
}
void solve(long long n)
{
for(int i = 0;i <= n;i++)
{
a[i] = quickpow(i,n,p) * ifac[i] % p;
b[i] = (i & 1 ? -1 : 1) * ifac[i];
}
init(n * 2),NTT(a),NTT(b);
for(int i = 0;i < limit;i++) a[i] *= b[i],a[i] %= p;INTT(a);
}
int main()
{
// freopen("input.in","r",stdin);
n = read(),init_fac(n);
if(n == 0){cout << 1 << endl;return 0;}solve(n);
for(int i = 0;i <= n;i++) cout << (a[i] % p + p) % p << ' ';
cout << endl;return 0;
}
```
同一列第二类斯特林数的计算:[P5396 第二类斯特林数·列](https://www.luogu.com.cn/problem/P5396)
### 十二重计数法
---
有 $n$ 个球和 $m$ 个盒子,要全部装进盒子里,求在不同限制条件下的方案数。
[P5824 十二重计数法](https://www.luogu.com.cn/problem/P5824)
#### 1. 球之间互不相同,盒子之间互不相同。
每个球都有 $m$ 种选择,根据乘法原理,共有 $n^m$ 种方案。
#### 2. 球之间互不相同,盒子之间互不相同,每个盒子至多装一个球。
我们第一个球有 $m$ 种放法,第二个有 $m−1$ 种,第三个有 $m−2$ 种,因此答案为 $m^{\underline{n}}$。
#### 3. 球之间互不相同,盒子之间互不相同,每个盒子至少装一个球。
我们令 **把 $n$ 个球装入 $m$ 个不同盒子,盒子可空** 的方案数为 $f(n,m)$,令 **把 $n$ 个球装入 $m$ 个不同盒子,盒子非空** 的方案数为 $g(n,m)$。
可以发现 $f(n,m)$ 即为这里的第一种情形,其答案为 $m^n$。但如果从盒子的角度考虑,我们可以用另一种方法表示 $f(n,m)$。枚举有 $i$ 个盒子非空,而这 $i$ 个盒子来自于原来 $m$ 个盒子,于是有 $C_m^i$ 种选择方法。累加把 $n$ 个小球放入 $i$ 个非空盒子的方案数即为 $f(n,m)$。联系到 $g(n,m)$ 的定义,这实际上累加的是 $g(n,i)$ 的值,即
$$
f(n,m)=\sum_{i=0}^mC_m^ig(n,i)
$$
我们对上式进行二项式反演,可得
$$
\begin{aligned}
g(n,m)&=\sum_{i=0}^mC_m^i(-1)^{n-i}f(n,i)\\
&=\sum_{i=0}^mC_m^i(-1)^{n-i}i^n
\end{aligned}
$$
#### 4. 球之间互不相同,盒子全部相同。
枚举有 $i$ 个盒子至少装了一个球,于是得到答案:
$$\text{ans} = \sum_{i=0}^m\begin{Bmatrix}n \\ i \end{Bmatrix}$$
直接用第二类斯特林数·行的模板即可,时间复杂度 $O(m \log m)$。
#### 5. 球之间互不相同,盒子全部相同,每个盒子至多装一个球。
首先若 $m<n$,即盒子数小于球数,那么显然无解。若 $m\ge n$,因为盒子是一样的,所以无论怎么装,都可以通过调换盒子顺序得到同一种解,而我们则将它们看作是一样的解。因此,答案为 $[n \le m]$。
#### 6. 球之间互不相同,盒子全部相同,每个盒子至少装一个球。
第二类斯特林数的定义,答案为 $\begin{Bmatrix}n \\ m \end{Bmatrix}$。
#### 7. 球全部相同,盒子之间互不相同。
因为盒子可以为空,我们先往盒子里各放一个球,最后拿走即可。然后采用隔板法,在 $n+m$ 个球所形成的 $n+m-1$ 个空隙中选 $m-1$ 个插入隔板,就得到了相对应的一种方案,方案数为 $C_{n+m-1}^{m-1}$。
#### 8. 球全部相同,盒子之间互不相同,每个盒子至多装一个球。
由于每个盒子只能装一个球,而每个球都要装到一个盒子里,于是答案为 $C_n^m$。
#### 9. 球全部相同,盒子之间互不相同,每个盒子至少装一个球。
插板法,即为在 $n$ 个球的 $n-1$ 个空隙中选 $m-1$ 个插上板,就得到了对应的一种分配方案,答案为 $C_{n-1}^{m-1}$。
#### 10. 球全部相同,盒子全部相同。
弱化版是 [P1025 数的划分](https://www.luogu.com.cn/problem/P1025),有一个显然的 dp 是定义 $f_{i,j}$ 表示将整数 $i$ 划分成不超过 $j$ 个正整数的方案数,则有递推式 $f_{i,j} = f_{i-j,j} + f_{i,j-1}$,最终答案为 $f_{n,m}$。但是时空复杂度都是 $O(n^2)$,可以利用生成函数相关的知识优化到 $O(n \log n)$。
#### 11. 球全部相同,盒子全部相同,每个盒子至多装一个球。
首先若 $m<n$,即盒子数小于球数,那么显然无解。若 $m\ge n$,因为盒子是一样的,所以无论怎么装,都可以通过调换盒子顺序得到同一种解,而我们则将它们看作是一样的解。因此,答案为 $[n \le m]$。
#### 12. 球全部相同,盒子全部相同,每个盒子至少装一个球。
和前面的 dp 是一样的,先给每个盒子一个球就好了,答案为 $f_{n-m,m}$。