已完成今日广义串并联图大学习
Lucyna_Kushinada
·
·
算法·理论
广义串并联图学习笔记
已完成今日广义串并联图大学习。
背景
2019 年,吴作同老师在集训队论文《公园》命题报告中,介绍了广义串并联图,自此广义串并联图开始在 OI 中逐渐走向普及。
定义
称满足对于任意 4 个节点都不存在 6 条两两没有公共边的路径连接这个节点中的每一对节点的无向连通图为广义串并联图。
更准确地说,就是不存在同胚于 K_4 的子图的无向连通图。
同胚,简单来说就是通过插入或删除 $2$ 度点(也称为**细分**或**平滑**操作)而得到的同构关系。
- **细分**:对于一条边 $(u,v)$,插入一个新点 $w$,将原来的边替换为 $(u,w)$ 和 $(w,v)$。形象一点就是从 `u-v` 到 `u-w-v`。
- **平滑**:细分操作的逆操作,将 `u-w-v` 变为 `u-v`。
它的名字叫广义串并联图,因为它的形态确实很像串并联电路。
## 图的生成
最简单的广义串并联图是两个点之间连一条边,也就是长度为 $1$ 的链。
对于一个广义串并联图 $G$,定义它的源汇点为指定的两个端点 $s,t$,通过 $s,t$ 这两个接口,能更好的定义广义串并联图的生成,记为 $G=(V,E,s,t)$。
那么那个最简单的广义串并联图可以记为 $G_0=({\{s,t\},\{(s,t)\}},s,t)\ (s\neq t)$。
首先得明确一个事实,广义串并联图只能由广义串并联图生成。
通过以下的一系列形象的操作搭配,可以从 $G_0$ 出发,生成任意一个广义串并联图。
### 串联
对于两个广义串并联图 $(V_1,E_1,s_1,t_1)$ 和 $(V_2,E_2,s_2,t_2)$。
可以将 $t_1$ 和 $s_2$ 合并为一个点。
得到新的广义串并联图 $(V_1\cup V_2/(t_1\sim s_2),E_1\cup E_2,s_1,t_2)$。
### 并联
对于两个广义串并联图 $(V_1,E_1,s_1,t_1)$ 和 $(V_2,E_2,s_2,t_2)$。
可以将 $s_1,s_2$,$t_1,t_2$ 各自合并。
得到新的广义串并联图 $(V_1\cup V_2/(s_1\sim s_2,t_1\sim t_2),E_1\cup E_2,s_1,t_1)$。
### 正确性证明
证明上述生成方式不会引入同胚于 $K_4$ 的子图:
首先对于任何与 $K_4$ 同胚的图,都满足删去任意 $\le 2$ 个节点,图仍然是保持连通,证明显然。
对于初态 $G_0$,显然没有同胚于 $K_4$ 的子图。
归纳地考虑,对于由两个广义串并联图 $G_1,G_2$ 合成的广义串并联图 $G$。
显然 $G_1,G_2$ 都不含与 $K_4$ 同胚的子图。
那么只需证这次合并操作不会引入与 $K_4$ 同胚的子图,显然如果想要有 $K_4$ 同胚的子图,则其顶点一定是一部分来自 $G_1$,另一部分来自 $G_2$,故只需要证明满足合并后,存在删除 $\le 2$ 个节点,会让图不连通。
对于串联操作,假设 $t_1=s_2=x$,那么 $x$ 显然是 $G$ 这张图的割点,只需删除这一个点 $x$,$G$ 就会不连通。
对于并联操作,假设 $s_1=s_2=x,t_1=t_2=y$,显然只有 $x,y$ 沟通了 $G_1,G_2$ 得到 $G$,只需删除这两个点 $x,y$,$G$ 就会不连通。
由此完成归纳,故上述生成方式一定不会引入同胚于 $K_4$ 的子图。
## 图的压缩
广义串并联图可以通过以下的操作变成一个单点:
- 删 $1$ 度点。对于一个 $deg(u)=1$ 的点 $u$,删去点 $u$ 以及 $u$ 唯一的连边 $(u,v)$。
- 缩 $2$ 度点。对于一个 $deg(u)=2$ 的点 $u$,记与其相邻的两个点 $x,y$,删除点 $u$ 以及边 $(u,x),(u,y)$,建立新边 $(x,y)$,比较像之前讲到的平滑操作。
- 叠合重边。选择两条重边,用一条边替换他们。
这也被称为广义串并联图方法。
这一部分的证明可以参考吴作同老师在 2019 年的集训队论文《公园》命题报告,里面给出了极为详细的证明。
## 性质
任意树,仙人掌图均是广义串并联图,原因显然。
广义串并联图是平面图,因为非平面图至少包含一个 $K_5$ 或者 $K_{3,3}$(左右部点数均为 $3$ 的完全二分图),而这两个东西都存在同胚于 $K_4$ 的子图。
广义串并联图在进行压缩操作中,每一条边都对应原图的一个子图,这很重要,这使得能够让边维护信息,在压缩操作的过程中合并。
此外,压缩操作中,每一个点也都对应原图的一个子图,同样能维护信息,在压缩操作的过程中合并。
在某些题目中,通过合理地设置边与点维护的信息(一般要求互不重叠),可以实现两者之间的交互,相互辅助维护对方的信息。
对于满足 $m\le n+k$ 的一般无向连通图,通过压缩操作,可以将图压缩到 $m\le 3k,n\le 2k$ 量级。
压缩的过程中,$m-n$ 单调不增,无法压缩时,一定有每个点的度数都 $\ge 3$,所以 $2m\ge 3n$,同时有 $m\le n+k$,解得 $m\le 3k,n\le 2k$,这使得某些题问题在压缩图之后,可以直接使用暴力做法解决。
## 【例题1】[P6790 [SNOI2020] 生成树](https://www.luogu.com.cn/problem/P6790)
### 题意
给定无向连通图 $G$,已知 $G$ 在删掉一条边后是一颗仙人掌,求 $G$ 的生成树个数。结果对 $998244353$ 取模。
$1 \le n \le m \le2 \times 10^5$。
### 题解
应该是广义串并联图方法模板题。
先证明题目中的图是广义串并联图,对于一个仙人掌,任意四个点之间至多有 $4$ 条两两没有公共边的路径,加上了一条边也至多 $5$ 条,所以这个图是广义串并联图。
利用广义串并联图在进行压缩操作中,每一条边都对应原图的一个子图的性质,可以通过一条边 $(u,v)$ 的连通与否出发,让其维护两个信息:
- $f_{(u,v)}$ 表示 $(u,v)$ 代表的子图中,使得 $u,v$ **连通**的生成树方案数。
- $g_{(u,v)}$ 表示 $(u,v)$ 代表的子图中,使得 $u,v$ **不连通**的生成森林方案数,显然 $u$ 和 $v$ 各自在一个生成树中,所以生成森林恰好包含两个生成树。
初始化全局答案为 $ans=1$,每条边 $(u,v)$ 的 $f_{(u,v)}=g_{(u,v)}=1$。
接下来按照广义串并联图方法,分三种情况转移:
**删 $1$ 度点**:
设当前点为 $u$,唯一的连边为 $(u,v)$。
通过 $(u,v)$ 的子图内部来让 $u,v$ 连通,一定会在所有的生成树方案中,直接,
$$ans\leftarrow ans\times f_{(u,v)}$$
**删 $2$ 度点**:
设当前点为 $u$,两条连边分别为 $(u,x)$ 和 $(u,y)$。
要让 $x,y$ 连通,则 $u,x$ 和 $u,y$ 都得连通,所以有,
$$f_{(x,y)}=f_{(u,x)}\times f_{(u,y)}$$
要让 $x,y$ 不连通,且恰好只产生两个生成森林,则 $u,x$ 和 $u,y$ 必须满足恰好一组连通,另一组不连通,所以有,
$$g_{(x,y)}=f_{(u,x)}\times g_{(u,y)}+g_{(u,x)}\times f_{(u,y)}$$
**叠合重边**:
不那么严谨地,设当前两条重边分别为 $(u_1,v_1)$ 和 $(u_2,v_2)$(实际上连接的两个点都一样,都是 $u,v$),设他们叠合后的边为 $(u,v)$。
此时有两种方式能让 $u,v$ 连通:通过 $(u_1,v_1)$ 代表的子图或 $(u_2,v_2)$ 代表的子图,但是为了满足树的形态,只能选择其中一种连通,而另一种不连通,所以有,
$$f_{(u,v)}=f_{(u_1,v_1)}\times g_{(u_2,v_2)}+g_{(u_1,v_1)}\times f_{(u_2,v_2)}$$
要让 $u,v$ 不连通,则在两个子图内都不应有 $u,v$ 连通,所以有,
$$g_{(u,v)}=g_{(u_1,v_1)}\times g_{(u_2,v_2)}$$
注意初始时重边的情况,此时可以在加边的的过程中就叠合掉,那么后续进行叠合重边,只会出现在删 $2$ 度点之后。
```cpp
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=(l);i<=(r);++i)
#define per(i,l,r) for(int i=(r);i>=(l);--i)
#define pr pair<int,int>
#define fi first
#define se second
#define pb push_back
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define bg(x) (x).begin()
#define ed(x) (x).end()
#define N 202508
#define int long long
const int mod=998244353;
int n,m,f[N],g[N],num;
map<int,pr>e[N];
inline void add(int u,int v,int f,int g){
if(e[u].count(v)){
pr &re=e[u][v];
re.fi=(re.fi*g%mod+re.se*f%mod)%mod;
re.se=re.se*g%mod;
e[v][u]=re;
return;
}
e[u][v]=e[v][u]={f,g};
}
signed main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
int ans=1;
rep(i,1,m){
int u,v;
cin>>u>>v;
add(u,v,1,1);
}
queue<int>q;
rep(i,1,n){
if(sz(e[i])<3){
q.push(i);
}
}
while(!q.empty()){
int u=q.front();
q.pop();
if(sz(e[u])==1){
auto re=*e[u].begin();
pr w=re.se;
ans=ans*w.fi%mod;
}
if(sz(e[u])==2){
auto rx=*e[u].begin();
auto ry=*next(e[u].begin());
int x=rx.fi,y=ry.fi;
pr wx=rx.se,wy=ry.se;
int f=wx.fi*wy.fi%mod;
int g=(wx.fi*wy.se%mod+wx.se*wy.fi%mod)%mod;
add(x,y,f,g);
}
for(auto v:e[u]){
int x=v.fi;
e[x].erase(u);
if(sz(e[x])<3){
q.push(x);
}
}
e[u].clear();
}
cout<<ans;
return 0;
}
```
## 【例题2】[P10779 BZOJ4316 小 C 的独立集](https://www.luogu.com.cn/problem/P10779)
### 题意
给定简单无向图 $G = (V, E)$,保证每条边属于且仅属于一个简单环,求 $G$ 的最大独立集大小。
$1\leq n\leq 5\times 10^4$,$1\leq m\leq 6\times 10^4$。
### 题解
主要启发在于对点和边分别设计贡献互不重叠的状态从而方便转移。
注意到 $G$ 是一个仙人掌,而仙人掌是广义串并联图,所以直接上广义串并联图方法,不断压缩图,最终变为一个单点,大概步骤如下:
- 删 $1$ 度点。对于一个 $deg(u)=1$ 的点 $u$,删去点 $u$ 以及 $u$ 唯一的连边 $(u,v)$。
- 缩 $2$ 度点。对于一个 $deg(u)=2$ 的点 $u$,记与其相邻的两个点为 $x,y$,删除点 $u$ 以及边 $(u,x),(u,y)$,建立新边 $(x,y)$,比较像之前讲到的平滑操作。
- 叠合重边。选择两条重边,用一条边替换他们。
利用压缩的过程中,每一条边都对应原图的一个子图的性质,套路地让每条边维护信息 $f_{u,v,0/1,0/1}$ 表示这条边所代表的子图中,$u,v$ 在或不在最大独立集中的情况下,最大独立集是多少。
然后你会发现删 $1$ 度点时,不太好转移贡献,而且这题也不能像 [P6790 [SNOI2020] 生成树](https://www.luogu.com.cn/problem/P6790) 那样直接把此时的贡献累计到答案里,考虑重新设计维护的信息。
具体地,还是设 $f_{u,v,0/1,0/1}$,不过此时它的含义是这条边所代表的子图中,$u,v$ 在或不在最大独立集中,且**不考虑** $u,v$ **自身的贡献**的情况下,最大独立集是多少。
同时,设 $a_{u,0/1}$ 表示选或不选 $u$ 计入最大独立集的情况下,$u$ 所代表的子图的最大独立集是多少。
这样的状态设计既保证了 $a$ 和 $f$ 的贡献互不重叠,同时也方便了转移。
接下来按照广义串并联图方法,分三种情况转移即可,这里不过多赘述。
需要注意的细节是,正向边的 $f_{0,1}$ 对应反向边的 $f_{1,0}$,$f_{1,0}$ 对应 $f_{0,1}$,加边的时候需要特殊处理,其他与反向边相同。
```cpp
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=(l);i<=(r);++i)
#define per(i,l,r) for(int i=(r);i>=(l);--i)
#define pr pair<int,int>
#define fi first
#define se second
#define pb push_back
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define bg(x) (x).begin()
#define ed(x) (x).end()
#define N 102508
#define int long long
int n,m,a[N][2],rt=1;
struct node{
int f00,f01,f10,f11;
};
map<int,node>e[N];
inline void add(int u,int v,int f00,int f01,int f10,int f11){
if(e[u].count(v)){
node &re=e[u][v];
re.f00+=f00;
re.f01+=f01;
re.f10+=f10;
re.f11+=f11;
e[v][u]=re;
swap(e[v][u].f01,e[v][u].f10);
return;
}
e[u][v]={f00,f01,f10,f11};
e[v][u]={f00,f10,f01,f11};
}
signed main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
rep(i,1,n){
a[i][0]=0;
a[i][1]=1;
}
rep(i,1,m){
int u,v;
cin>>u>>v;
add(u,v,0,0,0,-1e5);
}
queue<int>q;
rep(i,1,n){
if(sz(e[i])<3){
q.push(i);
}
}
while(!q.empty()){
int u=q.front();
q.pop();
if(sz(e[u])==1){
auto tmp=*e[u].begin();
int v=tmp.fi;
node re=tmp.se;
a[v][1]+=max(a[u][0]+re.f01,a[u][1]+re.f11);
a[v][0]+=max(a[u][0]+re.f00,a[u][1]+re.f10);
rt=v;
}
if(sz(e[u])==2){
auto tx=*e[u].begin(),ty=*next(e[u].begin());
int x=tx.fi,y=ty.fi;
node rx=tx.se,ry=ty.se;
int f00=0,f01=0,f10=0,f11=0;
f00=max(rx.f10+a[u][1]+ry.f10,rx.f00+a[u][0]+ry.f00);
f01=max(rx.f10+a[u][1]+ry.f11,rx.f00+a[u][0]+ry.f01);
f10=max(rx.f11+a[u][1]+ry.f10,rx.f01+a[u][0]+ry.f00);
f11=max(rx.f11+a[u][1]+ry.f11,rx.f01+a[u][0]+ry.f01);
add(x,y,f00,f01,f10,f11);
}
for(auto v:e[u]){
int x=v.fi;
e[x].erase(u);
if(sz(e[x])<3){
q.push(x);
}
}
e[u].clear();
}
cout<<max(a[rt][0],a[rt][1]);
return 0;
}
```
## 【例题3】[P4426 [HNOI/AHOI2018] 毒瘤](https://www.luogu.com.cn/problem/P4426)
### 题意
给定一个无向连通图,求该图的独立集方案数。
$n\le 10^5,n-1 \le m \le n+10$。
### 题解
跟上一题很像,所以状态设计其实大差不差,就是把最大独立集换成独立集方案数,同时边的状态定义不用特别声明排除端点的贡献,因为转移中本来就不会包含。
但这题的图并不是广义串并联图,不过可以发现 $m\le n+10$,即有 $k\le 10$,所以将这张图压缩后会满足 $m\le 30,n\le 20$,那么先用广义串并联图方法压缩一下,然后对剩下点的爆搜枚举是否在独立集里就行了。
```cpp
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=(l);i<=(r);++i)
#define per(i,l,r) for(int i=(r);i>=(l);--i)
#define pr pair<int,int>
#define fi first
#define se second
#define pb push_back
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define bg(x) (x).begin()
#define ed(x) (x).end()
#define N 102508
// #define M (1048576+10)
#define int long long
const int mod=998244353;
int n,m,a[N][2],p[N],cnt;
struct node{
int f00,f01,f10,f11;
};
map<int,node>e[N];
bitset<N>f,del;
inline void add(int u,int v,int f00,int f01,int f10,int f11){
if(e[u].count(v)){
node &re=e[u][v];
re.f00=(re.f00*f00)%mod;
re.f01=(re.f01*f01)%mod;
re.f10=(re.f10*f10)%mod;
re.f11=(re.f11*f11)%mod;
e[v][u]=re;
swap(e[v][u].f01,e[v][u].f10);
return;
}
e[u][v]={f00,f01,f10,f11};
e[v][u]={f00,f10,f01,f11};
}
signed main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
rep(i,1,n){
a[i][0]=a[i][1]=1;
}
rep(i,1,m){
int u,v;
cin>>u>>v;
add(u,v,1,1,1,0);
}
queue<int>q;
rep(i,1,n){
if(sz(e[i])<3){
q.push(i);
}
}
while(!q.empty()){
int u=q.front();
q.pop();
if(sz(e[u])==1){
auto tx=*e[u].begin();
int x=tx.fi;
node rx=tx.se;
a[x][0]=(rx.f00*a[u][0]%mod+rx.f10*a[u][1]%mod)%mod*a[x][0]%mod;
a[x][1]=(rx.f01*a[u][0]%mod+rx.f11*a[u][1]%mod)%mod*a[x][1]%mod;
del[u]=1;
}
else if(sz(e[u])==2){
auto tx=*e[u].begin(),ty=*next(e[u].begin());
int x=tx.fi,y=ty.fi;
node rx=tx.se,ry=ty.se;
int f00=0,f01=0,f10=0,f11=0;
f00=(
(rx.f00*a[u][0]%mod*ry.f00)%mod+
(rx.f10*a[u][1]%mod*ry.f10)%mod
)%mod;
f01=(
(rx.f00*a[u][0]%mod*ry.f01)%mod+
(rx.f10*a[u][1]%mod*ry.f11)%mod
)%mod;
f10=(
(rx.f01*a[u][0]%mod*ry.f00)%mod+
(rx.f11*a[u][1]%mod*ry.f10)%mod
)%mod;
f11=(
(rx.f01*a[u][0]%mod*ry.f01)%mod+
(rx.f11*a[u][1]%mod*ry.f11)%mod
)%mod;
add(x,y,f00,f01,f10,f11);
del[u]=1;
}
for(auto v:e[u]){
int x=v.fi;
e[x].erase(u);
if(sz(e[x])<3){
q.push(x);
}
}
e[u].clear();
}
rep(i,1,n){
if(del[i]){
continue;
}
p[++cnt]=i;
}
// cout<<rt<<"\n";
int tot=(1<<cnt)-1,ans=0;
rep(s,0,tot){
rep(i,1,cnt){
if(s>>(i-1)&1){
f[p[i]]=1;
}
}
int re=1;
rep(i,1,cnt){
int u=p[i];
re=re*a[u][s>>(i-1)&1]%mod;
for(auto v:e[p[i]]){
int x=v.fi;
node e=v.se;
if(x<=u){
continue;
}
if(f[u]&&f[x]){
re=re*e.f11%mod;
}
if(f[u]&&!f[x]){
re=re*e.f10%mod;
}
if(!f[u]&&f[x]){
re=re*e.f01%mod;
}
if(!f[u]&&!f[x]){
re=re*e.f00%mod;
}
}
}
rep(i,1,cnt){
if(s>>(i-1)&1){
f[p[i]]=0;
}
}
ans=(ans+re)%mod;
}
cout<<ans;
return 0;
}
```
## 【例题4】[P8426 [JOI Open 2022] 放学路 / School Road](https://www.luogu.com.cn/problem/P8426)
### 题意
给定一张 $n$ 个点 $m$ 条边的无向连通图,有边权。
请你判断是否存在一条 $1\to n$ 的**简单**路径,满足长度大于 $1\to n$ 的最短路长度。
$2\le n\le 10^5,m\le 2\times 10^5$。
### 题解
知识点:广义串并联图,点双连通分量,最短路。
好题啊。
可能会有的一个错误想法,是用单源最短路算法,分别求出最长路和最短路,然后比较一下,但这个图是不太能用单源最短路算法求最长路的,因为将边权取反后大概率会出现负环。
为了保证思维的流畅性,这里对每个子任务分别讲解。
### 子任务 1
$m\le 40$,直接暴力搜索即可,复杂度比较玄学,但是能过。
### 子任务 2
$n\le 18$,考虑状压 dp,求出**简单**路径中的最长路长度,最终和最短路比较一下。
前两个子任务对正解没什么提示性,毕竟不需要研究题目的任何性质。
### 子任务 3
令 $k=m-n$,则 $k\le 13$。
考虑转化题意,什么时候不存在题目所述的路径,就是 $1\to n$ 的所有路径的长度均相同的时候。
如果你学过广义串并联图方法,那么你应该会对这个条件非常敏感。
对这个图使用广义串并联图方法进行压缩后,会使得 $m\le 3k,n\le 2k$,而这个数据范围支持暴力搜索。
对于这题来讲,压缩的过程中,每条边 $(u,v)$ 维护的信息就是 $u\to v$ 路径长度 $w$,具体步骤如下:
- 删 $1$ 度点,设当前点为 $u$,只需要直接删除就行了,因为点不需要维护什么消息,它也无法贡献信息到其他边。
- 缩 $2$ 度点:设当前点为 $u$,记与其相邻的两个点为 $x,y$,那么直接删除旧边 $(u,x,w_x),(u,y,w_y)$,添加新边 $(x,y,w_x+w_y)$ 即可,这是不难理解的。
- 叠合重边:记连接两个点 $u,v$ 的两条重边分别为 $(u_1,v_1,w_1)$ 和 $(u_2,v_2,w_2)$,叠合后得到新边 $(u,v,w)$,那么如果 $w_1=w_2$,则 $w=w_1$,反之 $w=-1$,即标记为不合法,因为此时肯定存在两条 $u\to v$ 且长度不同的路径了。
特别地,上述步骤中的除了叠合重边 $u$ 和 $v$ 均不会是 $1$ 或者 $n$,也就是说 $1$ 和 $n$ 不参与上述前两种压缩方式。因为 $x$ 和 $y$ 可以为 $1$ 或 $n$,而叠合重边的操作,只会接在缩 $2$ 度点操作生成边 $(x,y,w_x+w_y)$ 的之后。
然后在压缩后的图上暴力搜索,如果存在一条经过过边权为 $-1$ 的边的 $1\to n$ 路径,那么说明肯定存在题目所说的路径。
### 子任务 4
这个条件看着比较抽象,其实就是想表达这张图是一张点双连通图,但似乎目前不太能知道这个条件有什么用。
考虑 子任务 3 解法的复杂度瓶颈,在于压缩完之后的那个搜索,能不能通过到一种方式,直接判定压缩后的图,是否存在题目所说的路径?
稍微手玩几组数据,可以初步猜测一个结论:
存在题目所说的路径,当且仅当压缩后的图只存在 $1$ 和 $n$ 两个点,且只有一条边 $(1,n,w)$,同时还满足 $w\neq -1$。
看着感觉确实很对啊,但是有以下一组 hack 数据:
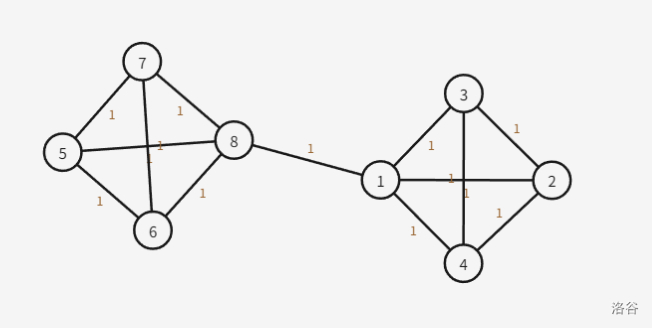
考虑为什么会错,因为图中的两个 $K_4$ 子图根本无法压缩,造成了误判的情况。
不过可以注意到,在这张图中,$1$ 和 $n$ 并不在同一个点双连通分量中。
正好这个子任务是点双连通图,不妨接着猜测,这种情况下,结论成立。
实际上,这个猜测是正确的,下面给出证明:
> 对于缩合后的图,若不是只有点 $1$ 和 $n$,且只有 $1$ 到 $n$ 一条边,那么这个图就一定存在同胚于 $K_4$ 的子图。\
此时若整个图是一个点双,则一定存在一个同胚于 $K_4$ 的子图且包含 $1$ 与 $n$,如果没有说明他们不在一个点双里,这与事实矛盾。\
在这种图中,因为边权 $\ge 1$,是无法保证每一条 $1$ 到 $n$ 路径长度均相同的(可以画一个 $K_4$ 自己理解一下)。证毕。
### 正解
先用 `dijkstra` 跑出 $1\to n$ 的最短路长度 $d$,加入新边 $(1,n,d)$,显然并不影响答案,只是会使得 $1$ 和 $n$ 在同一点双连通分量中,方便处理。
使用 `tarjan` 处理出同时包含 $1$ 和 $n$ 的点双连通分量点集 $S$。
建立一个新图,原图中的边 $(u,v,w)$ 出现在新图中当且仅当 $u\in S,v\in S$,显然这个新图是一个点双连通图。
为什么只需要考虑同时包含 $1$ 和 $n$ 的这个点双连通分量,因为其他的点与边加入与否都不可能会贡献一条新的从 $1$ 到 $n$ 的路径(否则就在这个点双里了),也不会降低连通度。
然后用广义串并联图方法压缩这个新图。
然后判断压缩后的图是否只存在 $1$ 和 $n$ 两个点,且只有一条边 $(1,n,w)$,同时还满足 $w\neq -1$ 即可。
```cpp
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=(l);i<=(r);++i)
#define per(i,l,r) for(int i=(r);i>=(l);--i)
#define pr pair<int,int>
#define fi first
#define se second
#define pb push_back
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define bg(x) (x).begin()
#define ed(x) (x).end()
#define N 202508
#define int long long
int n,m;
struct edge{
int t,w;
};
vector<edge>g[N];
bitset<N>f;
namespace ssp{
int dis[N];
inline void dijkstra(int s){
rep(i,1,n){
f[i]=0;
dis[i]=1e18;
}
dis[s]=0;
priority_queue<pr,vector<pr>,greater<pr>>q;
q.push({dis[s],s});
while(!q.empty()){
int u=q.top().se;
q.pop();
if(f[u]){
continue;
}
f[u]=1;
for(edge x:g[u]){
if(dis[u]+x.w<dis[x.t]){
dis[x.t]=dis[u]+x.w;
q.push({dis[x.t],x.t});
}
}
}
}
inline int run(){
dijkstra(1);
return dis[n];
}
}
map<int,int>e[N];
inline void add(int u,int v,int w){
if(e[u].count(v)){
int &re=e[u][v];
if(re==-1){
return;
}
re=(re==w)?w:-1;
e[v][u]=re;
return;
}
e[u][v]=e[v][u]=w;
}
int st[N],tp,dfn[N],low[N],num,id;
vector<int>scc[N];
inline void dfs(int k,int fa){
dfn[k]=low[k]=++num;
st[++tp]=k;
for(edge x:g[k]){
if(x.t==fa){
continue;
}
if(!dfn[x.t]){
dfs(x.t,k);
low[k]=min(low[k],low[x.t]);
if(low[x.t]>=dfn[k]){
id++;
do{
scc[id].pb(st[tp]);
tp--;
}while(st[tp+1]!=x.t&&tp);
scc[id].pb(k);
}
}
else{
low[k]=min(low[k],dfn[x.t]);
}
}
}
inline void init(){
int dis=ssp::run();
g[1].pb({n,dis});
g[n].pb({1,dis});
dfs(1,0);
f.reset();
int pos=0;
rep(i,1,id){
for(int x:scc[i]){
f[x]=1;
}
if(f[1]&&f[n]){
pos=i;
break;
}
for(int x:scc[i]){
f[x]=0;
}
}
for(int x:scc[pos]){
f[x]=1;
}
for(int x:scc[pos]){
for(edge y:g[x]){
if(!f[y.t]){
continue;
}
add(x,y.t,y.w);
}
}
}
signed main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
rep(i,1,m){
int u,v,w;
cin>>u>>v>>w;
g[u].pb({v,w});
g[v].pb({u,w});
}
init();
queue<int>q;
rep(i,1,n){
if(sz(e[i])<3){
q.push(i);
}
}
while(!q.empty()){
int u=q.front();
q.pop();
if(u==1||u==n){
continue;
}
if(sz(e[u])==2){
pr tx=*e[u].begin(),ty=*next(e[u].begin());
add(tx.fi,ty.fi,tx.se+ty.se);
}
for(pr v:e[u]){
int x=v.fi;
e[x].erase(u);
if(sz(e[x])<3){
q.push(x);
}
}
e[u].clear();
}
// cout<<sz(e[1])<<' '<<e[1].count(n)<<' '<<e[1][n]<<"\n";
if(sz(e[1])==1&&e[1].count(n)&&e[1][n]!=-1){
cout<<0;
}
else{
cout<<1;
}
return 0;
}
```
## [【例题5】P10044 [CCPC 2023 北京市赛] 最小环](https://www.luogu.com.cn/problem/P10044)
### 题意
给定一张 $n$ 个点 $m$ 条边的带权弱联通有向图。
求这张图的最小环。
$n\le 3\times 10^5$,$\color{#ee7959}{-1\le m-n \le 1500}$。
### 题解
好题。
知识点:~~广义串并联图~~,最短路。
$-1\le m-n \le 1500$,很难不让人联想到广义串并联图,但是这题并不是无向图,不能套用老一套的广义串并联图方法。
但是这个数据范围还是太色了,不妨根据题目的性质,尝试发明一套新的方法:
- 删除**只有**出度或者入度的点。因为题目要求最小环,而这样的点是不可能在环里的。
- 缩出度和入度均为 $1$ 的点。将到两端点的边权相加,合成一个不包含它的新边,再把这个点删掉。因为如果这个点在最小环中,那么一定会同时经过与它连接的两条边。
- 叠合重边。对于重边只保留边权最小的,在最小环的题设下,这是一个显然的支配关系。
一直操作直到不能进行任何上述操作,设此时图的边数为 $m$,点数为 $n$。
显然剩下的点一定存在入度和出度,且出入度之和 $\ge 3$,而一条边会贡献 $1$ 个入度和 $1$ 个出度共 $2$ 个度数,所以显然存在 $2m\ge 3n$。
联立题目条件 $m-n\le 1500$,解得 $n\le 3000,m\le 4500$。
此时就可以暴力求最小环了,具体地,枚举点 $u$ 作为环上一点,跑从它出边的点出发的最短路即可。
注意进行缩出度和入度均为 $1$ 的点的操作时,如果这个点出边和入边都指向一个点,那就直接跳过,不然会出一些奇奇怪怪的错误。
```cpp
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=(l);i<=(r);++i)
#define per(i,l,r) for(int i=(r);i>=(l);--i)
#define pr pair<int,int>
#define fi first
#define se second
#define pb push_back
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define bg(x) (x).begin()
#define ed(x) (x).end()
#define N 300010
#define int long long
int n,m,ans=1e18;
unordered_map<int,int>g[N],ig[N];
struct edge{
int t,w;
};
vector<edge>e[N];
inline void add(int u,int v,int w){
if(g[u].count(v)){
g[u][v]=min(g[u][v],w);
ig[v][u]=g[u][v];
return;
}
g[u][v]=w;
ig[v][u]=w;
}
vector<int>vec;
inline void build(){
rep(i,1,n){
if(!sz(g[i])){
continue;
}
vec.pb(i);
for(pr u:g[i]){
vec.pb(u.fi);
e[i].pb({u.fi,u.se});
// cout<<i<<' '<<u.fi<<' '<<u.se<<"\n";
}
}
sort(all(vec));
vec.erase(unique(all(vec)),ed(vec));
}
int dis[N];
bitset<N>f;
inline int calc(int s){
for(int i:vec){
dis[i]=1e18;
f[i]=0;
}
priority_queue<pr,vector<pr>,greater<pr>>q;
for(edge x:e[s]){
dis[x.t]=x.w;
q.push({x.w,x.t});
}
while(!q.empty()){
int u=q.top().se;
q.pop();
if(f[u]){
continue;
}
f[u]=1;
for(edge x:e[u]){
if(dis[u]+x.w<dis[x.t]){
dis[x.t]=dis[u]+x.w;
q.push({dis[x.t],x.t});
}
}
}
return dis[s];
}
signed main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
rep(i,1,m){
int u,v,w;
cin>>u>>v>>w;
if(u==v){
ans=min(ans,w);
continue;
}
add(u,v,w);
}
queue<int>q;
rep(i,1,n){
if(!sz(ig[i])||!sz(g[i])||(sz(ig[i])==1&&sz(g[i])==1)){
q.push(i);
}
}
while(!q.empty()){
int u=q.front();
q.pop();
// cout<<u<<" del\n";
if(!sz(ig[u])||!sz(g[u])){
;//ok I see u r here, then go DIE :)
}
else if(sz(ig[u])==1&&sz(g[u])==1){
pr tx=*ig[u].begin(),ty=*g[u].begin();
int x=tx.fi,y=ty.fi;
int wx=tx.se,wy=ty.se;
if(x==y){
continue;
}
// cout<<u<<' '<<x<<' '<<y<<' '<<wx+wy<<" two\n";
add(x,y,wx+wy);
}
for(pr v:g[u]){
int x=v.fi;
ig[x].erase(u);
g[x].erase(u);
if(!sz(ig[x])||!sz(g[x])||(sz(ig[x])==1&&sz(g[x])==1)){
q.push(x);
}
}
for(pr v:ig[u]){
int x=v.fi;
ig[x].erase(u);
g[x].erase(u);
if(!sz(ig[x])||!sz(g[x])||(sz(ig[x])==1&&sz(g[x])==1)){
q.push(x);
}
}
g[u].clear();
ig[u].clear();
}
build();
// assert(sz(vec)<=5000);
for(int i:vec){
ans=min(ans,calc(i));
}
if(ans>=1e18){
cout<<"-1";
return 0;
}
cout<<ans;
return 0;
}
```