前缀和与差分

· · 题解

从一维差分到二维差分超详细题解，并严格遵守题解审核要求。

一、题意简述

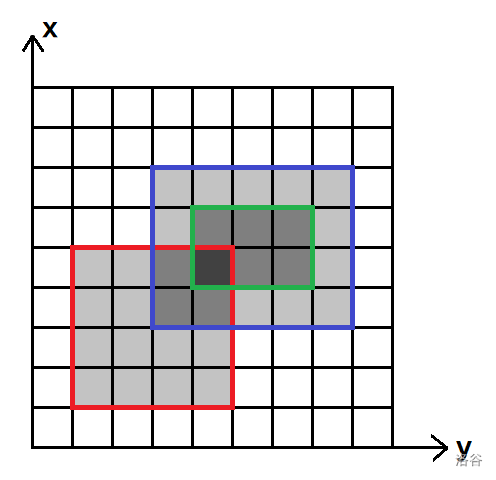
每个格子被覆盖的次数用格子颜色的深浅直观地表现了出来。

只要数一数有多少个格子刚好被 k 个矩形覆盖，就能求出答案。

2.较慢的方法

怎么求出每个格子被多少矩形覆盖了呢？最基本的思路是对每个矩形，将它覆盖的格子全都加上1。这种方法最坏情况复杂度是 O(x2y2n)，大约需要 10^{11} 次操作，显然会超时。代码就不贴了。

3.一维差分前缀和

如果变成一维数组区间加，应该就能想到办法：线段树 差分+前缀和。（会的同学可直接跳至“5.二维差分前缀和”）

比如下面这张图，黑色和红色组成的柱子表示原数组，其中红色部分就是它的差分数组：

用公式表示就是：（差分简称 c，前缀和简称 q）

c_1=a_1 c_{i}=a_{i}-a_{i-1}(i>1) q_{1}=a_1 q_{i}=\sum_{k=1}^{i} a_{k}=q_{i-1}+a_{i}(i>1)

显然，差分与前缀和互为逆运算。

4.一维区间加

比如我们知道了一个数组 a 的差分数组 b，怎么才能快速地操作数组 b，使数组 a 的区间 [x,y] 加上 v 呢？

我们可以先区间加，再差分，找到规律。比如第二行是第一行的差分数组，第三行是将第一行第3-5项都加上v，第四行是第三行的差分。

[a_1,a_2,a_3,a_4,a_5,a_6,a_7,a_8] [a_1,a_2-a_1,a_3-a_2,a_4-a_3,a_5-a_4,a_6-a_5,a_7-a_6,a_8-a_7] [a_1,a_2,a_3+v,a_4+v,a_5+v,a_6,a_7,a_8] [a_1,a_2-a_1,a_3-a_2+v,a_4-a_3,a_5-a_4,a_6-a_5-v,a_7-a_6,a_8-a_7]

可以看到，第四行与第二行的区别只在第3个数和第6个数，于是能得到这样的算法：

c[left]+=v;
c[right+1]-=v;

所以需要进行大量的区间加时，可以先进行差分，O(1) 的区间加，再前缀和回来。

5.二维差分前缀和

二维前缀和也很好定义。

q_{i,j}=\sum_{k=1}^i\sum_{l=1}^j a_{k,l}

但是差分显得不很直观，所以需要用差分是前缀和的逆运算的特点推。

\because \text{红}+\text{橙}+\text{黄}+\text{灰}=(\text{红}+\text{橙})+(\text{橙}+\text{黄})-\text{橙}+\text{灰} \text{即}q_{i,j}=q_{i-1,j}+q_{i,j-1}-q_{i-1,j-1}+a_{i,j} \therefore a_{i,j}=q_{i,j}+q_{i-1,j-1}-q_{i,j-1}-q_{i-1,j} \therefore c_{i,j}=a_{i,j}+a_{i-1,j-1}-a_{i,j-1}-a_{i-1,j}\text{（此处用到了差分和前缀和互为逆运算的特点）}

由第三个式子顺便得到前缀和的递推式：

q_{i,j}=q_{i,j-1}+q_{i-1,j}-q_{i-1,j-1}+a_{i,j}

6.二维区间加

二维区间加我们仍然按照上面的方法推，但是用字母太麻烦，所以下面用数字。一下四个矩阵意义仍与上同，第三个的红色部分为 [(1,1),(2,2)] 加上5的部分，第四个的红色部分为与第二个不同的数。

\begin{bmatrix}8&9&10&5&7\\5&4&9&4&5\\6&3&3&3&3\\9&8&8&5&4\\5&10&4&3&2\end{bmatrix} \begin{bmatrix}3&2&-4&0&1\\-1&2&5&-5&1\\-3&-2&0&3&1\\4&-6&6&-2&0\\5&5&-6&-1&-1\end{bmatrix} \begin{bmatrix}8&9&10&5&7\\5&4&9&4&5\\6&\color{red}8&\color{red}8&3&3\\9&\color{red}13&\color{red}13&5&4\\5&10&4&3&2\end{bmatrix} \begin{bmatrix}3&2&-4&0&1\\-1&\color{red}-3&5&\color{red}0&1\\-3&-2&0&3&1\\4&\color{red}-1&6&\color{red}-7&0\\5&5&-6&-1&-1\end{bmatrix}

可以看到，上面矩阵的-1和0是由1-和-5加5得到的，-3和-7是由2和-2减5得到的，所以可以得到如下算法：（x_1,x_2,y_1,y_2 意义如题）

c[x1][y1]+=v;
c[x2][y2]+=v;
c[x1][y2]-=v;
c[x2][y2]-=v;

7.最终做法

建立一个差分数组，一个原数组，读入每个矩形，用上述方法对差分数组操作实现区间加1。最后将差分数组进行前缀和得到原数组，统计 k 的个数，得到答案。

三、代码

#include<iostream>
using namespace std;
int n,k,ans,c[1010][1010],a[1010][1010];
//n,k意义如题，ans是答案，c是差分数组，a是原数组
int main()
{
    cin>>n>>k;
    for(int i=1;i<=n;i++)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        c[x1][y1]++;//二维差分区间加
        c[x2][y2]++;//
        c[x1][y2]--;//
        c[x2][y1]--;//
    }
    for(int i=0;i<=1005;i++)
        for(int j=0;j<=1005;j++)
        {
            a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+c[i][j];//前缀和的递推式
            if(a[i][j]==k)ans++;//恰被覆盖k次，统计
        }
    cout<<ans<<endl;
    return 0;
}