题解:CF2111F Puzzle
CJZJC
·
·
题解
我们假设构造出来的图形周长为 $p\times i$,面积为 $s\times i$。
发现这个周长比面积非常恶心,考虑固定一个判断另一个是否可以。
考虑用到小学老师教过的平移法。
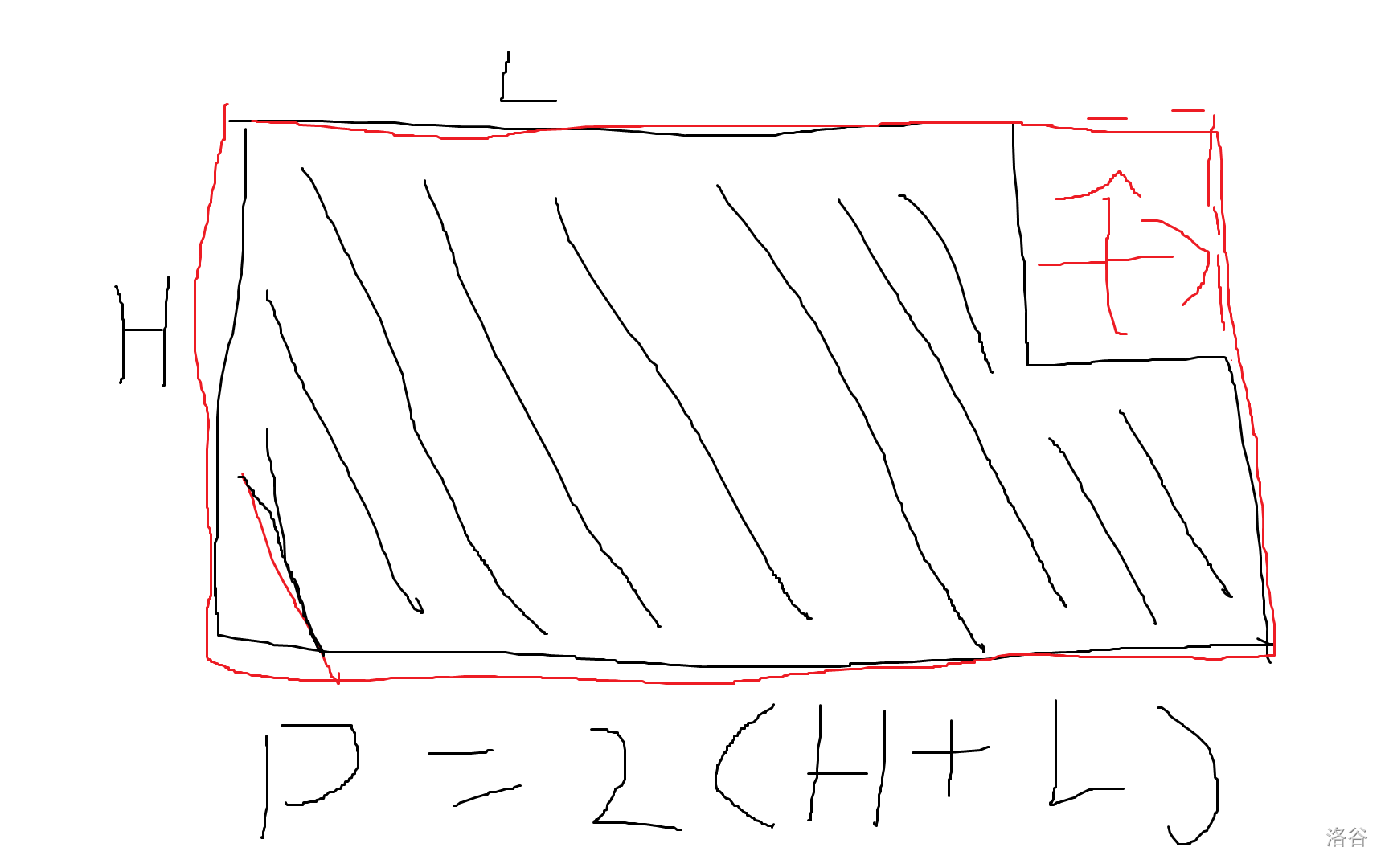
在长方形里挖掉一块后它的周长不变。
那么我们只要枚举周长 $p\times i$,再判断能否放下 $s\times i$ 的面积就可以了。
复杂度大概是 $O(i^2p)$,实际更快。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long
int T,s,p;
signed main(){
cin>>T;
while(T--){
cin>>p>>s;
int tmp=__gcd(p,s);
p/=tmp;
s/=tmp;
if(p>s*4){
cout<<"-1\n";
continue;
}
bool fl=0;
for(int i=1;s*i<=50000;i++){
int c=p*i;
if(c%2!=0){
continue;
}
for(int j=1;j<c/2;j++){
int h=j,l=c/2-j;
if(h*l<s*i){
continue;
}
if(s*i<h+l-1){
continue;
}
fl=1;
cout<<s*i<<'\n';
for(int i=1;i<=l;i++){
cout<<1<<' '<<i<<'\n';
}
for(int i=2;i<=h;i++){
cout<<i<<' '<<1<<'\n';
}
int tmp=s*i-l-h+1;
for(int i=2;i<=h;i++){
for(int j=2;j<=l;j++){
if(tmp){
cout<<i<<' '<<j<<'\n';
tmp--;
}
else{
break;
}
}
if(!tmp){
break;
}
}
break;
}
if(fl){
break;
}
}
if(!fl){
cout<<"-1\n";
}
}
}
```