[ARC156F] Make Same Set 题解
Schi2oid
·
·
题解
题意简述
给三个长度为 N 的序列 A,B,C,现在要求你找到一个最大的集合,使得以下两种方式都可以将其构造出来:
- 对于所有 i,将 A_i 或 B_i 加入集合。
- 对于所有 i,将 A_i 或 C_i 加入集合。
### 思路分析
将上述约束弱化,我们将两种方式改为:
- 对于所有 $i$,将 $A_i$ 或 $B_i$ 加入集合或什么都不做。
- 对于所有 $i$,将 $A_i$ 或 $C_i$ 加入集合或什么都不做。
那么,对于这个约束,我们有一个显然的网络流解法:
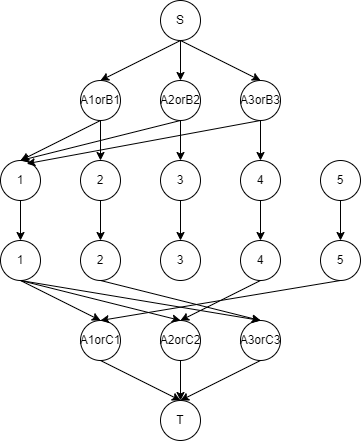
我们称上图中第一排点为 $AB$ 点,第 $i$ 个表示我们需要在 $A_i$ 和 $B_i$;称上图中最后一排点为 $AC$ 点,第 $i$ 个点表示我们需要在 $A_i$ 和 $C_i$;第二排点和第三排点分别表示 $AB$ 和 $AC$ 点选择的值,称其为中间点。我们对于 $AB$ 点和 $AC$ 点连向与它们挨着的那一排中的 $A_i,B_i$ 或是 $A_i,C_i$ 连边。其他连边如上图所示,所有连边的流量都为 $1$。那么,对于这个网络,我们跑最大流,就可以找到一组解。
那么考虑这个最大流跑出来的结果有可能有什么问题。考虑对于一个 $AB$ 点或一个 $AC$ 点,若与它相连的中间点都没有流经过,那么我们实际上就是在这一次选择时什么都没做,那么我们就不知道这个点应该选择哪一个。我们定义这样的点为**待定点**。如下图,红色的反边表示这条路径被流过了,那么标记为方形的点就是**待定点**,这是因为它们连向的中间点都不在红色路径上。
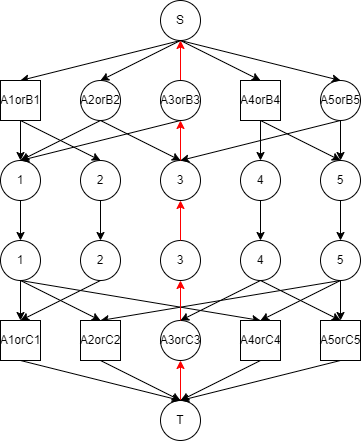
现在,我们考虑一条怎样的增广路才会导致图中产生新的**待定点**。这意味着,存在与这个点相连的中间点从被流经变成了没有被流经。也就是说,我们在这条增广路图中一定能够找到一段路径,它从一个 $AC$ 点出发,接下来经过两个中间点,然后抵达某个 $AB$ 点。只有这种情况才会将某一段路径从被流经过改为没有被流经过。由于与这个点相连的点都没有被流经,那么这个点本身也一定没有被流经,即其与 $S$ 或 $T$ 之间的连边是可选的。这时,我们可以直接让这个点连接 $S$ 或 $T$ 点,再连向中间点,之后的路径不变。此时增广路长度一定会变短。
如下图所示,如果我们选择红色的增广路,那么它就会产生下图中标记为菱形的新的**待定点**。发现一条 $\text{A3orC3}\rightarrow 3 \rightarrow 3 \rightarrow \text{A3orB3}$ 的路径,这条路径状态的变更使得这个菱形点变成了一个**待定点**。这时,我们可以直接对这条增广路调整为右图中的蓝色增广路,这样,增广路长度变小,同时让这个菱形结点不再成为新的**待定点**。
这说明,如果对于一条增广路,其会造成某个点变成新的**待定点**,那么一定存在另外一条增广路比它更短。换句话来说,**如果对最短的增广路进行增广,则一定不会产生新的待定点**。

得到这一结论,我们只需要构造一张图,使得其上不存在任何的**待定点**,然后跑一遍最大流即可,显然我们可以在最开始直接钦定我们每一次选择都是 $A_i$。由于每一个 $AB$ 点一定会与一个代表 $A_i$ 的中间相连,而所有 $A_i$ 都被流经,所以图上不存在任何**待定点**。
至此本题完结,复杂度 $O(N\sqrt N)$。
### 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int INF=1e18;
int a[5005],b[5005],c[5005];
int n,m=10000,S=0,T;
int AB(int x){return x;}
int AC(int x){return x+n+2*m;}
int ABv(int x){return x+n;}
int ACv(int x){return x+n+m;}
int nxt[200005],head[200005],to[200005],val[200005];
int cnt=1;
int visa[200005],visv[200005];
int cur[200005];
void build(int u,int v,int w){
to[++cnt]=v;
val[cnt]=w;
nxt[cnt]=head[u];
head[u]=cnt;
to[++cnt]=u;
val[cnt]=w^1;
nxt[cnt]=head[v];
head[v]=cnt;
}
int dep[200005];
queue<int>q;
bool bfs(){
memcpy(cur,head,sizeof head);
q.push(S);
for(int i=0;i<=2*n+2*m+1;i++) dep[i]=-1;
dep[S]=0;
while(!q.empty()){
int u=q.front();
q.pop();
for(int eg=head[u];eg;eg=nxt[eg]){
int v=to[eg];
if(!val[eg]||dep[v]!=-1) continue;
q.push(v);
dep[v]=dep[u]+1;
}
}
return dep[T]!=-1;
}
int dfs(int x,int in){
if(x==T) return in;
int out=0;
for(int ed=cur[x];ed;ed=nxt[ed]){
cur[x]=ed;
if(!val[ed]||dep[to[ed]]!=dep[x]+1) continue;
int tmp=dfs(to[ed],min(val[ed],in-out));
val[ed]-=tmp;
val[ed^1]+=tmp;
out+=tmp;
if(out==in) break;
}
return out;
}
int dinic(){
int ret=0;
while(bfs()){
ret+=dfs(S,INF);
}
return ret;
}
int ans[200005];
signed main(){
cin>>n;
T=2*n+2*m+1;
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
if(!visv[a[i]]){
visv[a[i]]=1;
visa[i]=1;
}
}
for(int i=1;i<=n;i++) scanf("%lld",&b[i]);
for(int i=1;i<=n;i++) scanf("%lld",&c[i]);
for(int i=1;i<=n;i++){
build(S,AB(i),visa[i]?0:1);
build(AB(i),ABv(a[i]),visa[i]?0:1);
build(AB(i),ABv(b[i]),1);
build(ACv(a[i]),AC(i),visa[i]?0:1);
build(ACv(c[i]),AC(i),1);
build(AC(i),T,visa[i]?0:1);
}
for(int i=1;i<=m;i++) build(ABv(i),ACv(i),visv[i]?0:1);
dinic();
for(int i=1;i<=n;i++){
int node=AB(i);
if(val[head[node]]) ans[a[i]]=1;
else ans[b[i]]=1;
}
int anscnt=0;
for(int i=1;i<=m;i++) if(ans[i]) anscnt++;
printf("%lld\n",anscnt);
for(int i=1;i<=m;i++) if(ans[i]) printf("%lld ",i);
puts("");
return 0;
}
```