题解 P3388 【模板】割点(割顶)
wind_seeker
·
·
题解
下面即为图示过程:
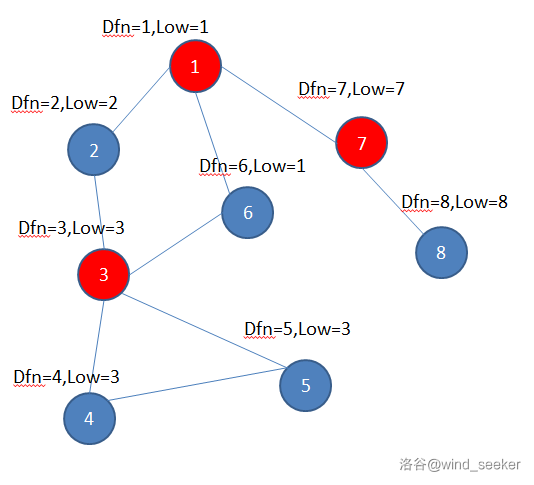
$1$ 为根,扫到 $3$ 和 $7$ 的时候 $3$ 和 $7$ 都没访问过,则 $1$ 有两个子树,所以 $1$ 为割点。
$7$ 与 $3$ 一样,满足 $low_8\ge dfn_7$,为割点。
#### code
```cpp
void tarjan(int u,int anc){
dfn[u]=low[u]=++dfncnt;
int child=0;
for(auto v:g[u]){
if(!dfn[v]){
tarjan(v,anc),low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]&&u!=anc) cut[u]=true;//如果儿子的low值大于等于dfn,则代表其为儿子与其他非子树点相连的唯一途径
if(u==anc) child++;
}
else low[u]=min(low[u],dfn[v]);
}
if(child>=2&&u==anc) cut[u]=true;//对根的处理
```
- 难点:
对于割点,很多初学者都会对于 `low[u]=min(low[u],dfn[v])` 感觉奇怪,然而将其改为 `low[u]=min(low[u],low[v])` 后,又会寄,这是因为问题出现在了割点上。
下图即为错误例子(取 `low[u]=min(low[u],low[v])`):
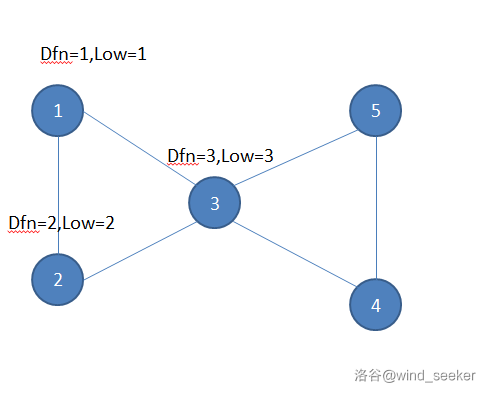
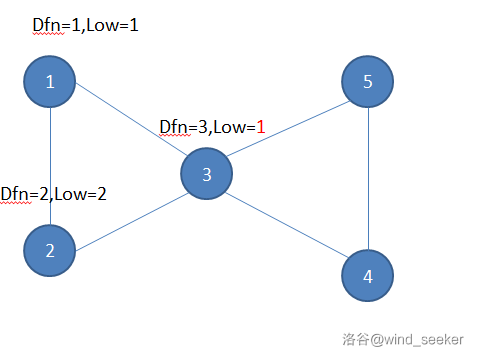
$3$ 通过回溯 $1$ 而获得了 $low_3=1$。


$4$ 通过回溯 $3$ 而获得了 $3$ 的 $low$ 值,变成了 $low_4=1$。那么就不能判断 $3$ 为割点了。
- 难点证明:
证明前提是其不是一条链,不然没有意义。由于割点同时与割后的两个图相连,它的 $low$ 值必然是两个图中较小的 $low$ 值。假设我们取 `low[u]=min(low[u],low[v])`,若后遍历的图的割点的儿子 $v$ 可回溯至割点,那么就会把割点的 $low$ 值传递回 $v$,那么它的 $low$ 值就不正确了。
证明了 `low[u]=min(low[u],low[v])` 的错误,我们也来证明一下 `low[u]=min(low[u],dfn[v])` 的正确性。由于儿子未遍历情况的取小值的方式,我们知道 $low$ 值是可以传递回去的。那么其实对于 $v$ ,它只要可以搜索到**一个**比 $u$ 时间戳小的点即可,不必通过该点继续往上寻找即可证明 $u$ 为割点,所以这也是具有正确性的。
### code
```cpp
/* let life be like summer flowers */
/* by wind_seeker */
/* 2023-03-07 21:13 */
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=2e4+1e3;
inline int read(){
int res=0,f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) res=(res<<3)+(res<<1)+(c^48);
return res*f;
}
int n,m,ans;
vector<int> g[N];
bool cut[N];
int dfn[N],low[N],dfncnt;
int st[N],top;
bool inst[N];
void tarjan(int u,int anc){
dfn[u]=low[u]=++dfncnt;
int child=0;
for(auto v:g[u]){
if(!dfn[v]){
tarjan(v,anc),low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]&&u!=anc) cut[u]=true;//如果儿子的low值大于等于dfn,则代表其为儿子与其他非子树点相连的唯一途径
if(u==anc) child++;
}
else low[u]=min(low[u],dfn[v]);
}
if(child>=2&&u==anc) cut[u]=true;//对根的处理
}
int main(){
n=read(),m=read();
for(int i=1,u,v;i<=m;i++){
u=read(),v=read();
g[u].pb(v);g[v].pb(u);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i,i);
for(int i=1;i<=n;i++)
if(cut[i]) ans++;
printf("%d\n",ans);
for(int i=1;i<=n;i++)
if(cut[i]) printf("%d ",i);
return 0;
}
/*
6 7
1 2
1 3
1 4
2 5
3 5
4 5
5 6
*/
/*
1
5
*/
```