浅谈 Tarjan 算法
Zhl2010
·
·
算法·理论
前置
一大堆名词
关于图的名词
强连通:
在一个有向图里,由 a 有一条路可以走到 b,由 b 又有一条路可以走到 a,我们就叫这两个顶点 (a,b) 强连通。
强连通图:
如果 在一个有向图 G 中,每两个点都强连通,我们就叫这个图,强连通图。
强连通分量:
在一个有向图 G 中,有一个子图,这个子图每 2 个点都满足强连通,我们就叫这个子图叫做强连通分量。
关于 Tarjan
$dfn_{~}$:每个点的时间戳。
$low_{~}$:不经过其父亲能到达的最小的时间戳。
---
# 正文
## 强连通分量 - 有向图
强连通分量:SCC。
### 思路:
- 1,储存 $dfn$ 与 $low$ 值,初始化 $dfn_x=low_x=0$。
- 2,用栈存储新出现的节点,依次遍历每个子节点,每次都更新最小值保证子树根最小。
- 3,若找到 $dfn_x=low_x$,则 $x$ 为本强连通分量中的根节点,将 $x$ 及比 $x$ 后进栈的元素出栈,为一个强连通分量。
### 代码
```cpp
void tarjan(int x){
dfn[x]=low[x]=++cnt;//记录时间戳
s.push(x);
vis[x]=1;
for(int i=0;i<e[x].size();i++){//枚举每个子结点
int q=e[x][i];
if(!dfn[q]){//套板子
tarjan(q);
low[x]=min(low[x],low[q]);
}else if(vis[q])low[x]=min(low[x],dfn[q]);
}
if(low[x]==dfn[x]){//判定是强连通分量
gs++;//强连通分量数++
while(s.top()!=x){
int t=s.top();
s.pop();//用了就弹出
num[gs]++;//强连通分量的个数增加
vis[t]=0;//记录其已经属于一个强连通分量了
}
s.pop();//同上
num[gs]++;
vis[x]=0;
}
}
```
### 例题
- [P2863 \[USACO06JAN\] The Cow Prom S](https://www.luogu.com.cn/problem/P2863)
---
## 缩点
先看模板题:[P3387 【模板】缩点](https://www.luogu.com.cn/problem/P3387)
### 题目描述
给定一个 $n$ 个点 $m$ 条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。
### 思路
首先题目允许重复走,所以我们可以知道,只要走上了强连通分量的任意一个点,整个强连通分量都可以走过。
所以我们可以想到将整个强连通分量看成一个点,也就是**缩点**。
我们新建一个图,保存缩完后的图,强连通分量缩成的点为强连通分量每个点的权值和。
最后用 Topo 或 SPFA 算出答案。
### 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
stack<int>s;
int n,m,cnt=0,ti,top,cn=0;
int p[10010],head[10010],sd[10010],dfn[10010],low[10010];
int stac[10010],vis[10010],vi[10010];
int h[10010],in[10010],dis[10010];
struct node{
int to,next,from;
}edge[100010],ed[100010];
void add(int x,int y){
edge[++cnt].next=head[x];
edge[cnt].from=x;
edge[cnt].to=y;
head[x]=cnt;
}
void tarjan(int x){
low[x]=dfn[x]=++ti;
s.push(x);
vis[x]=1;
for(int i=head[x];i;i=edge[i].next){
int v=edge[i].to;
if(!dfn[v]) {
tarjan(v);
low[x]=min(low[x],low[v]);
}else if(vis[v]){
low[x]=min(low[x],low[v]);
}
}
if(dfn[x]==low[x]){
int y;
while(1){
y=s.top();
s.pop();
sd[y]=x;
vis[y]=0;
if(x==y) break;
p[x]+=p[y];
}
}
}
int topo(){
queue <int> q;
int tot=0;
for(int i=1;i<=n;i++){
if(sd[i]==i&&!in[i]){
q.push(i);
dis[i]=p[i];
}
}
while(!q.empty()){
int k=q.front();q.pop();
for(int i=h[k];i;i=ed[i].next){
int v=ed[i].to;
dis[v]=max(dis[v],dis[k]+p[v]);
in[v]--;
if(in[v]==0) q.push(v);
}
}
int ans=0;
for(int i=1;i<=n;i++)ans=max(ans,dis[i]);
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&p[i]);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
}
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);
for(int i=1;i<=m;i++){//新建图
int x=sd[edge[i].from],y=sd[edge[i].to];
if(x!=y){
ed[++cn].next=h[x];
ed[cn].to=y;
ed[cn].from=x;
h[x]=cn;
in[y]++;
}
}
cout<<topo()<<endl;
return 0;
}
```
### 例题
- [P3387 【模板】缩点](https://www.luogu.com.cn/problem/P3387)
- [P2341 \[USACO03FALL / HAOI2006\] 受欢迎的牛 G](https://www.luogu.com.cn/problem/P2341)
- [P2812 校园网络【\[USACO\] Network of Schools 加强版】](https://www.luogu.com.cn/problem/P2812)
- [T335409 0x67-Tarjan 算法与有向图连通性 - 银河](https://www.luogu.com.cn/problem/T335409)
---
## 割点(割顶)
### 模板题
- [P3388 【模板】割点(割顶)](https://www.luogu.com.cn/problem/P3388)
给出一个 $n$ 个点,$m$ 条边的无向图,求图的割点。
### 样例分析(什么是割点)
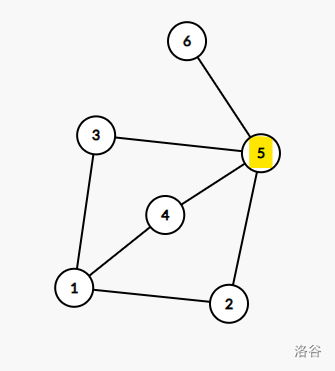
上图是这题样例,首先找割点。
**割点定义**:对于一个无向图,如果把一个点删除后这个图的极大连通分量数增加了,那么这个点就是这个图的割点。
按照定义,图中 $5$ 号节点就是割点,如果它断了,他连的边就断了,这个图就不止原先的一个强连通分量了。
### 思路
首先可以发现:如果 $y$ 是 $x$ 的子节点且 $low(y) \ge dfn(x)$,那么 $x$ 就是割点。
$y$ 在不经过 $(x,y)$ 的情况下只能到达比 $x$ 更晚访问到的节点,所以删去边 $(x,y)$ 后,$y$ 必定与比 $x$ 更早访问到的点不相连,就会分裂成一张不联通的子图。
但是对于根节点,这是不对的,因为根节点的子节点没法到比根节点时间戳更小的节点,所以会将根节点误判成割点。
所以对根判定方法为:
> 若 $s$ 有两颗及以上的子树,那么 $s$ 即为割点。
割掉 $s$ 后,它的所有子树之间互不联通,所以 $s$ 为割点。
### 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<int>e[100010];
int ti=0,dfn[100010],low[100010],cnt=0;
int an[100010];
void tarjan(int x,int root){
dfn[x]=low[x]=++ti;
int child=0;
for(int i=0;i<e[x].size();i++){
int q=e[x][i];
if(!dfn[q]){
child++;
tarjan(q,root);
low[x]=min(low[x],low[q]);
//cout<<x<<' '<<low[q]<<' '<<dfn[x]<<endl;
if(low[q]>=dfn[x]&&x!=root){//不是根的点的判断
an[x]=1;
}
}else low[x]=min(low[x],dfn[q]);
}
if(child>=2&&x==root)an[x]=1;//对根的特判
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
for(int i=1;i<=n;i++)if(!dfn[i]) tarjan(i,i);
int ans=0;
for(int i=1;i<=n;i++){
if(an[i])ans++;
}
cout<<ans<<endl;
for(int i=1;i<=n;i++){
if(an[i])cout<<i<<' ';
}
return 0;
}
```
### 例题:
- [P3388 【模板】割点(割顶)](https://www.luogu.com.cn/problem/P3388)
---
## 割边:
定义:
> 对于一个无向图,如果删掉一条边后图中的连通分量数增加了,则称这条边为桥或者割边。
思路与割点差不多,只是 $low(y) \ge dfn(x)$ 改成了 $low(y) > dfn(x)$,而且不用考虑根节点了。
### 代码(例题炸铁路)
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<int>e[100010];
int ti=0,dfn[100010],low[100010],f[100010],cnt=0;
struct node{
int x,y;
}an[100010];
void add(int x,int y){
an[++cnt].x=x;
an[cnt].y=y;
}
void tarjan(int x){
dfn[x]=low[x]=++ti;
for(int i=0;i<e[x].size();i++){
int q=e[x][i];
if(!dfn[q]){
f[q]=x;
tarjan(q);
low[x]=min(low[x],low[q]);
//cout<<x<<' '<<low[q]<<' '<<dfn[x]<<endl;
if(low[q]>dfn[x]){
add(x,q);
}
}else if(q!=f[x]) low[x]=min(low[x],dfn[q]);
}
}
bool cmp(node a,node b) {
if(a.x==b.x)return a.y<b.y;
return a.x<b.x;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
for(int i=1;i<=n;i++)if(!dfn[i]) tarjan(i);
sort(an+1,an+cnt+1,cmp);
for(int i=1;i<=cnt;i++){
cout<<an[i].x<<' '<<an[i].y<<endl;
}
return 0;
}
```
### 例题
- [P1656 炸铁路](https://www.luogu.com.cn/problem/P1656)
---
## 边双连通分量
### 模板题
- [P8436 【模板】边双连通分量](https://www.luogu.com.cn/problem/P8436)
对于一个 $n$ 个节点 $m$ 条无向边的图,请输出其边双连通分量的个数,并且输出每个边双连通分量。
### 定义
> 连通图:任意两个结点都可以相互到达的无向图。
> 桥:一张连通图中,如果删去任意一条边会导致图不连通,则这条边就称为桥。
> 边双连通图:一个没有桥的连通图。
> 边双连通分量:极大的边双连通子图。
## 思路
边双连通分量和强连通分量十分类似,要改的地方:
- 因为是无向图,所以不需要考虑横叉边,因此不需要 $vis$ 来判断是否在栈中,而是直接 else。
- 无向图的边我们一般看成是两条有向图的边,但是这样就会导致一个问题:这样会被看成是一个环。所以我们需要加一个判断:不能访问上一个被访问过的结点。
- 最后答案可以用一个二维 vector 存起来。
$\huge{但是}$ 只有 $50$ 分,为什么?
- 数据是有重边的,而重边就可以往回走了。但是我们这个判断就直接把这个机会给干掉了。
- 因此,我们不能根据顶点来判断,而是要根据边来判断,条件是不能走上一次走过的边。我们为了判边,就需要给 vector 多加上一个 int 保存边的编号来判断。
### 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m;
int cnt;
int dfn[500050], low[500050];
vector<pair<int,int> >e[500050];
vector<vector<int> >ans;
stack<int> s;
void tarjan(int x,int las){
low[x]=dfn[x]=++cnt;
s.push(x);
for (int j=0;j<e[x].size();j++){
int i=e[x][j].first;
if (e[x][j].second==las) continue;
if (!dfn[i]){
tarjan(i,e[x][j].second);
low[x]=min(low[x],low[i]);
}else low[x]=min(low[x],dfn[i]);
}
if (dfn[x]==low[x]){
vector<int> vec;
vec.push_back(x);
while(s.top()!=x){
vec.push_back(s.top());
s.pop();
}
s.pop();
ans.push_back(vec);
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int a,b;
scanf("%d%d",&a,&b);
e[a].push_back({b,i});
e[b].push_back({a,i});
}
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i,0);
cout<<ans.size()<<endl;
for(int j=0;j<ans.size();j++){
vector<int>i=ans[j];
cout<<i.size()<<' ';
for (int k=0;k<i.size();k++){
int z=i[k];
cout<<z<<' ';
}
cout<<endl;
}
return 0;
}
```
### 例题
- [P8436 【模板】边双连通分量](https://www.luogu.com.cn/problem/P8436)
- [P2860 \[USACO06JAN\] Redundant Paths G](https://www.luogu.com.cn/problem/P2860)
---
## 点双连通分量
~~题目越来越恶心…~~
### 模板题
对于一个 $n$ 个节点 $m$ 条无向边的图,请输出其点双连通分量的个数,并且输出每个点双连通分量。
### 思路
点双连通分量:指在无向图中,如果去掉任意一个节点都不会破坏图的连通性,即极大的不包含割点的连通块被称为点双连通分量。
结论:
> 每个割点至少属于两个点双连通分量。
> 两个点双连通分量之间一定有割点。
证明:
如果该点不是割点,那么整个图就是一个点双,点与点之间可以相互到达。与两个点双不符,故两个点双之间一定有割点,该割点至少属于两个点双。
按之前求割点的做法求出割点,在割点判断成功后,记录答案,也是用栈到之前的点,用二维数组记录。
### 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<int>e[5000010];
int ti=0,dfn[5000010],low[5000010],cnt=0;
int an=0;
vector<int> ans[5000010];
//stack<int>s;
int s[5000010];
int top=0;
void tarjan(int x,int root){
dfn[x]=low[x]=++ti;
int child=0;
//s.push(x);
s[++top]=x;
for(int i=0;i<e[x].size();i++){
int q=e[x][i];
if(!dfn[q]){
child++;
tarjan(q,x);
low[x]=min(low[x],low[q]);
if(low[q]>=dfn[x]){
an++;
//while(s.top()!=q){
while(s[top+1]!=q){
//ans[an].push_back(s.top());
ans[an].push_back(s[top--]);
//s.pop();
}
ans[an].push_back(x);
}
}else if(q!=root)low[x]=min(low[x],dfn[q]);
}
if(root==0&&child==0)ans[++an].push_back(x);
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
for(int i=1;i<=n;i++)if(!dfn[i]) {
top=0;
tarjan(i,0);
}
cout<<an<<endl;
for(int i=1;i<=an;i++) {
cout<<ans[i].size()<<' ';
for(int j=0;j<ans[i].size();j++) cout<<ans[i][j]<<' ';
cout<<endl;
}
return 0;
}
```
### 例题
- [P8435 【模板】点双连通分量](https://www.luogu.com.cn/problem/P8435)
---
终于讲完了糖浆(tarjan)算法 😊!!!
$\Huge{🎉🎉🎉🎉🎉🎉}