题解:P6579 [Ynoi2019] Happy Sugar Life
jerry1717
·
·
题解
提供一种离线线性空间的写法,跑的超级快,完全没有卡常最大点都小于时限的一半。
题意
## 做法
由于非强制在线,考虑拆分贡献。以值为 $y$ 坐标,下标为 $x$ 坐标建立坐标图,将一次询问抽象成这样:
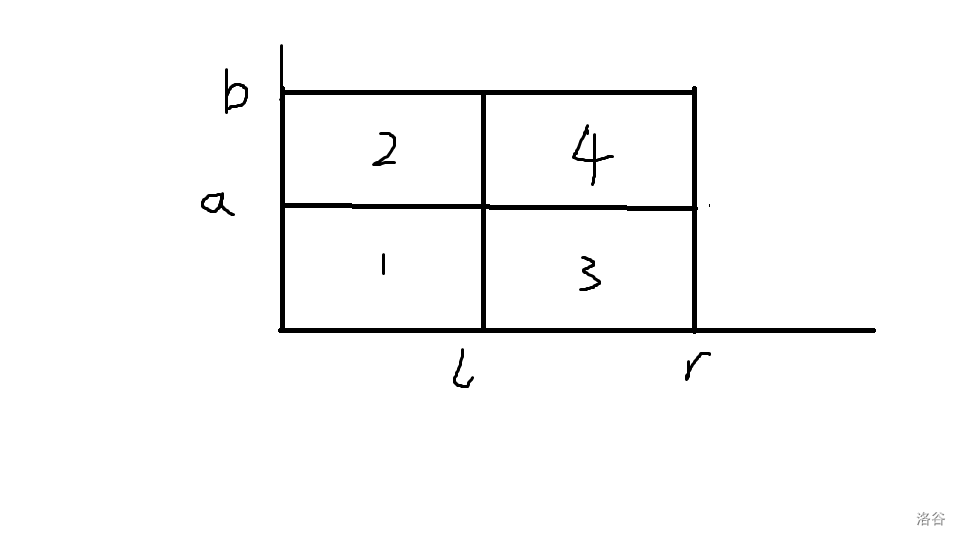
及求第四部分内的顺序对数量。记我们的顺序对为 $(i,j)$,先考虑只有 $j$ 有必要在第四部分内的总贡献 —— 对原图做一次扫描线算出每个点有多少个在之前的逆序对,在做一次扫描线算出只有 $j$ 在第四部分内的总贡献。
因为我们不仅算了 $a$ 在第四部分的贡献,也算了 $a$ 在第一二三部分的贡献,所以需要容斥。
$a$ 在第一部分:发现所有在第一部分的点都会对在第二部分的点产生贡献,区间二维数点后乘起来直接减掉就好了。
难点在于 $a$ 位于第二或第三部分的贡献。因为我们前面根本没用到根号算法,所以肯定是分块。
第二第三部分实质上是一样的,以第三部分为例,将区间分块,发现尽管对于块内贡献的本质不同的询问不超过 $O(B^2)$ 个,我们预处理也会爆空间,需要逐块处理。我们记 $f_{l,r}$ 表示值域 $[l,r]$ 中的顺序对数量,我们发现 $f_{i,j-1}$ 可以拆分成 $f_{i+1,j-1}$ 加上 $i$ 对区间 $[i+1,j-1]$ 的贡献,$f_{i+1,j}$ 又可以拆分为 $f_{i+1,j-1}$ 加上 $j$ 对 $[i+1,j-1]$ 的贡献。这样我们发现 $f_{i+1,j}+f_{i,j-1}-f_{i+1,j-1}$ 与 $f_{i,j}$ 只相差了 $i$ 与 $j$ 产生的贡献,这样我们就得到了转移方程,用类似于区间动态规划的写法预处理即可。用 $f_{1,b}-f_{a,b}-f_{1,a}$ 就能得出块内第三个部分对第四部分的贡献。
至于散块与整块之间和整块到整块之间的贡献,记值 $dn$ 表示小于 $a$ 的数的个数,从左到右枚举,然后用值域在 $[a,b]$ 之间的数一乘就做完了,记得更新 $dn$ 的值要在计算贡献之后,因为块内的贡献我们上一步算完了。
对于第二部分,我们不妨用同样的方法做(因为保证了是个排列)也可以统计出贡献。
这样就做完了这道分块题。
## 代码
代码其实不难写,想要的可以私信我。