题解 P4714 【「数学」约数个数和】
WinXP
·
·
题解
这是一篇 其实我不怎么敢提交的 画风优良,言之成理,语义清晰,老少咸宜,不涉及到数学名词 和高难算法!,并且不掺杂大量公式 是个人就能看懂 的题解
本题解的目的在于让该题目成为浅蓝题 我会尽量最清晰的解释自己的思路,如果还是不懂,可能你现在不适合这样的题目(绝对不是我说不明白),可以考虑加任务计划以后做。看不懂中文看式子,看不懂式子读中文,都看不懂出门左转
(用\prod_{i=1}^n表示从1到n乘在一起,用\sum_{i=1}^n表示加在一起)
如果你已经知道怎么做并且只是好奇这个奇怪标题的原因倒着看就好了
首先,通过 不是数竞生所以可以随便大力猜结论的暴力打表 严谨的证明,我们发现这是一个积性函数。
至于证明看其他人的就好了(虽然我觉得没有什么用反正你也会不证作为oier要用好自己的工具就是计算机乖乖打表啊对吧
你不会积性函数?
(两者有区别,要仔细区分)
也就是说,n 的答案 等于 n 质因数分解之后,每一个 质数的次幂 的答案 的乘积。因为它们都是质数所以自然两两互质。
用数学来表示,即把一个任意的积性函数的值记为 G_a ,把 a 表示为p_1^{q_1}p_2^{q_2}p_3^{q_3}...p_m^{q_m} (我,或者说大家习惯用p表示质数),有
G_a=G_{p_1^{q_1}}G_{p_2^{q_2}}G_{p_3^{q_3}}...G_{p_m^{q_m}}
我们把这道题的答案计为 f_k^a , 对a质因数分解可以得到
a=\prod_{i=1}^m p_i^{qi}
就有了
f_k^a=\prod_{i=1}^mf_k^{(p_i^{qi})}
为什么要变成这样的形式呢?
因为 考虑对于f_k^{(p_i^{qi})}怎么搞。
如果你真的读题了就能写出这样的式子
f_k^a=\sum_{x|a}f_{k-1}^x
当这个式子中的 $a=p_i^{qi}$ 时,就变成了
$$f_k^{(p_i^{qi})}=\sum_{t=1}^{qi}f_{k-1}^{(p_i^{t})}$$
因为显然对于一个质数的 $q$ 次幂,是他的约数的只有这个质数的 大于等于 $0$ 小于等于$p$ 的次幂。
注意到这个时候其实 $pi$ 已经没有用了,只要它是一个质数就可以,无论是$2$或者$5$~~或者19260817~~值都是一样的。那我们干脆把 $pi$ 删掉来表示。
$$F_k^{n}=\sum_{t=1}^{n}F_{k-1}^{t}$$
这个就是把开始化成这个形式的原因。(我说的有点墨迹,一般想到是积性函数就能想到这里吧 $QAQ$ )
看起来感觉好多了。可以非常明晰的看出来,每一维的 $k$ 都是在求 $k-1$ 维的前缀和。所以现在~~如果不是大常选手~~我们就已经有了 $11$ 分。
这个转移这么蠢,它一定是有规律的。~~(要不然怎么A)~~
我们来反着考虑这个问题。
假如把 $k$ 这个下标规定为最小值为$-2$ , 且当 $k=-2$ 时只有一个$F_{-2}^1$的值等于$1$,$F_{-2}^x (x!=1)$的值全部为 $0$ 。 那么根据定义我们就有 $F_{-1}^x=1$,$F_0^x=x$。考虑 $F_{-2}^1$ 对答案会贡献多少次,或者说考虑自低往上的转移,进而考虑最终的答案。
换句话说,把每一个状态看做一个矩阵上的点对,把每一层的转移都想象成 一条有向边 连向转移目标点 的话,(即从 $(x,t)$ 连向($(x,t+1)$ 到 $(n,t+1)$) 的所有的点) , 我们就是在考虑一个开始的点$(1,-2)$能有多少种方式走到最后的目标点 $n$ 。
emmmmm
大概像这样
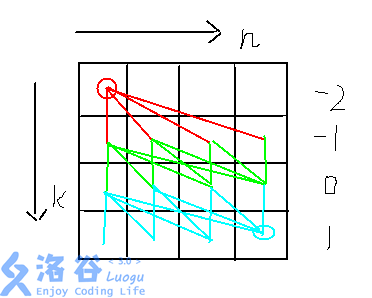
我们可以~~通过惊人的眼力~~发现路径数目为 $6$(用的是画图 见谅。。)
(其实引入图论只是帮助理解,不是正解非得从图论上考虑,~~话说这其实是小学奥数题啊~~)
我们发现一共转移了 $k+2$ 次 。每一次转移都由*当前状态转移到相等或更大的值*。如果把每一次转移考虑为在*当前状态上加上一个非负整数*,它就变成了一个人尽皆知通俗易懂的问题:
有
$$1+x_1+x_2+...+x_{k+2}=n,(xi>=0)$$
求方案数。
即可运用插板法解决得到 $C_{n+k}^{k+1}$ 。
(什么是插板法?......)
首先考虑在每一个x上加1,就变成了
$$x_1+x_2+...+x_{k+2}=n-1+(k+2),(xi>=1)$$
这个问题等价于把长度为 $(n+k+1)$ 的区间 分成 $(k+2)$ 份 > 等价于在 $(n+k)$ 个点中选取 $(k+1)$ 个来分割这个区间。
来整理一下答案。
总的答案:
$$f_k^a=\prod_{i=1}^mf_k^{(p_i^{qi})}$$
答案的每一项:
$$f_k^{(p_i^{qi})}=\sum_{t=1}^{qi}f_{k-1}^{(p_i^{t})}$$
进行两次问题转化,变为求组合数:
$$f_k^{(p_i^{qi})}=F_k^{qi}=\sum_{t=1}^{qi}F_{k-1}^{t}=C_{qi+k}^{k+1}$$
$$f_k^a=\prod_{i=1}^m C_{qi+k}^{k+1}$$
等等,有一个问题。这个组合数怎么求?$qi$ 是一个数的指数,再大也不会很大,当 $pi=2$ 的时候 $qi$ 的最大值才为 $60$ 左右。不过 $k$ 可是异常的大啊。肯定不能求出 $(qi+k)$ 的阶乘。
随便举个例子。设想求 $C_8^6=C_8^2=\frac{8!}{2!6!}=\frac{7*8}{1*2}$ 。我们并不需要求 $(qi+k)$ 的阶乘,只需要求 $(qi+k)$ 中的后 $(qi-1)$ 项除去前 $(qi-1)$ 项就好了。 所以为了处理除,我们需要一个逆元。不行,我实在写不动了,逆元不会自行百度吧....
逆元随便怎么求都可以。我们发现求组合数的复杂度其实是相当小的,而复杂度关键在于哪里呢?
分解质因数。标准的分解质因数是枚举质数,如果发现 $n$ 是这个质数的倍数,就除干净,计n不是这个质数的倍数除了几次即为这一项的次数。优化一下,枚举质数的时候可以枚举到 $\sqrt n$ 的大小。因为大于这个数的质数,如果是 $n$ 的约数,一定是一次,因为它的平方就已经比 $n$ 大了。同理大于 $\sqrt n$ 的质数也一定只有一个。
但是当 $n$ 为 $1e18$ 的时候我们发现 $1e9$ 的范围是不可过的
所以我们需要Miller-Rabin或Pollad-rho算法 吗?
~~no no no 想想出题人要是卡会怎么卡你? 肯定放几个筛不出来的大质数的乘积对吧 因为1s线筛大概能筛1e7 所以这几个质数显然都是1e8 1e9 的量级 这个量级的质数常用的有几个 你还不明白吗~~
```cpp
#include <bits/stdc++.h>
#define rap(i,s,n) for(int i=s;i<=n;i++)
#define drap(i,s,n) for(int i=s;i>=n;i--)
#define N 111111
#define P 998244353
#define ll long long
#define m(s,k) memset(s,k,sizeof s)
using namespace std;
ll n,k;
int prime[N],cnt;
bool isnt[N];
void Prime(int n){
rap(i,2,n){
if(!isnt[i]) prime[++cnt]=i;
rap(j,1,cnt){
if(prime[j]*i>cnt) break;
isnt[i*prime[j]]=1;
if(i%prime[j]==0) break;
}
}
}
ll ans=1,inv[N];
ll C(int x){ll res=1; rap(i,1,x) res=res*inv[i]%P*((x+k%P+2-i)%P)%P; return res;}
int main(){
cin>>n>>k; inv[1]=1; rap(i,2,100000) inv[i]=inv[P%i]*(P-P/i)%P;
Prime(100000); prime[++cnt]=998244353; prime[++cnt]=1000000007; prime[++cnt]=1000000009;
rap(j,1,cnt){
int v=prime[j]; if(v*v>n) break;
if(n%v==0){
int t=0;
while(n%v==0) n/=v,t++;
ans=ans*C(t)%P;
}
}
if(n>1) ans=ans*C(1)%P;
printf("%lld\n",ans);
return 0;
}
```
~~sans:像你这样的孩子应该在地狱里燃烧~~