P7915 [CSP-S 2021] 回文 题解
I_am_Accepted
·
·
题解
比 T2 简单的 T3 这辈子不多了……
感觉我的做法挺简单的。
分析
由于每一步只能从 \{a\} 的两端之一取一个数字放在 \{b\} 的末尾,所以对第一步的操作分类。
这里只考虑第一步取 'L' 的情况,第一步取 'R' 的情况就不再赘述(除字典序外思路相同)。
找到有且仅有的那个 x 满足 1<x\leqslant 2n \ and \ a_1=a_x。
由于 b_1 对应 a_1,则必然 b_{2n} 对应 a_x,即 \{a\} 中 a_x 最后一个被取到。
于是题目转化成:
$d$ 是一个元素**从底至顶**为 $a_{x+1}\to a_{2n}$ 的栈。
`'L'`表示取出 $c$ 的栈顶元素,`'R'`表示取出 $d$ 的栈顶元素,求**使得两个栈的取出序列回文**的**字典序最小**的操作序列。
突然变简单了……
把 $c$ 和 $d$ 都看作双端队列(即栈底可以取出元素)。
重复作这两个步骤直至 $c,d$ 皆为空:
1. 找到一个既存在于 $c,d$ 的(一个或两个)栈顶,又存在于 $c,d$ 的(一个或两个)栈底的元素,若有两个这样的元素,优先选择存在于 $c$ 栈顶的那个(字典序最小)。若找不到,输出 $-1$ 表示无解。
2. 栈顶和栈底各删掉一个这个元素,更新操作序列。
晕了?举个例子(样例 palin1.in 中第一组):
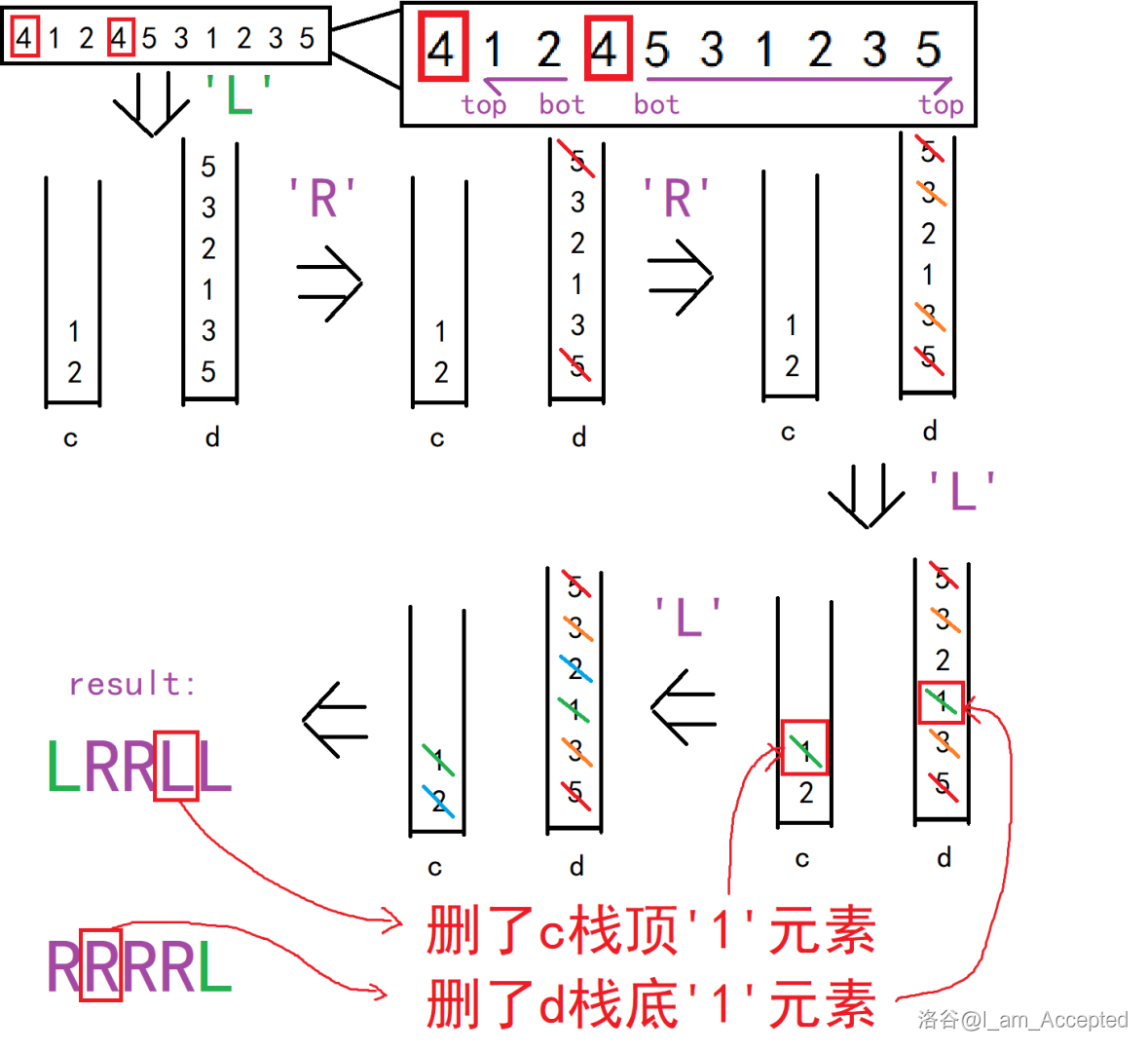
$O(n)$ 解决问题。
### Code
冗长的考场代码 qwq。
```cpp
#include<bits/stdc++.h>
using namespace std;
#define For(i,j,k) for(register int i=j;i<=k;i++)
#define Rof(i,j,k) for(register int i=j;i>=k;i--)
#define N 1000010
int n;
int v[N];
char ans[N],cur[N];
struct sta{
int s[N],l,r;
int L(){return s[l];}
int R(){return s[r-1];}
void push(int x){s[r++]=x;}
void pL(){l++;}
void pR(){r--;}
void clear(){l=r=0;}
bool empty(){return r==l;}
int size(){return r-l;}
}a,b;
int see(int l,int r,int val){
For(i,l,r)
if(v[i]==val)
return i;
return -1;
}
void check(){
int now=2;
while(1){
if(a.empty() && b.empty()){
break;
}else if(b.empty()){
if(a.L()!=a.R()){
cur[1]='Z';
return ;
}
cur[now]=cur[2*n-now+1]='L';
a.pL();
a.pR();
}else if(a.empty()){
if(b.L()!=b.R()){
cur[1]='Z';
return ;
}
cur[now]=cur[2*n-now+1]='R';
b.pL();
b.pR();
}else{
if(a.R()==a.L() && a.size()>1){
cur[now]=cur[2*n-now+1]='L';
a.pL();
a.pR();
}else if(a.R()==b.L()){
cur[now]='L';
cur[2*n-now+1]='R';
b.pL();
a.pR();
}else if(b.R()==a.L()){
cur[now]='R';
cur[2*n-now+1]='L';
a.pL();
b.pR();
}else if(b.R()==b.L() && b.size()>1){
cur[now]='R';
cur[2*n-now+1]='R';
b.pL();
b.pR();
}else{
cur[1]='Z';
return ;
}
}
now++;
}
}
bool pan(){
int id=1;
while(id<=2*n && cur[id]==ans[id]) id++;
return id<=2*n && cur[id]<ans[id];
}
signed main(){
int T;
scanf("%d",&T);
int pos;
while(T--){
ans[1]='Y';
scanf("%d",&n);
For(i,1,2*n) scanf("%d",v+i);
a.clear();
b.clear();
pos=see(2,2*n,v[1]);
Rof(i,pos-1,2) a.push(v[i]);
For(i,pos+1,2*n) b.push(v[i]);
cur[1]='L';
cur[2*n]='L';
check();
if(pan()){
For(i,1,2*n) ans[i]=cur[i];
}
a.clear();
b.clear();
pos=see(1,2*n-1,v[2*n]);
Rof(i,pos-1,1) a.push(v[i]);
For(i,pos+1,2*n-1) b.push(v[i]);
cur[1]='R';
cur[2*n]='L';
check();
if(pan()){
For(i,1,2*n) ans[i]=cur[i];
}
if(ans[1]=='Y'){
printf("-1\n");
}else{
For(i,1,2*n) printf("%c",ans[i]);
printf("\n");
}
}
return 0;
}
```