eJOI2021 Xcopy 题解
Licykoc
·
·
题解
reference: eJOI2021 Day1 Editorial
可以猜测此时可行的最优解是 $2^m - 1$,考虑构造。
- 如果 $m = 2^k (k \in \mathbb N_+)$,那么可以构造出 $\forall 0 \le i \le n - 1, a_i \gets i \oplus (i >> 1)$。这其实就是格雷码,其一性质就是可任意 `rotate`。
- 否则将 $m$ 拆成 $2^{k_1} + 2^{k_2} + \cdots +2^{k_p},(k_1\gt k_2 \gt \cdots \gt k_p)$,单个 $2^{k_i}$ 按照上述做法构造,同时其中每个元素要加上 $2 ^ {k_1} + \cdots + 2^{k_{i-1}}$,这样就能保证没有重复元素。接下来需要合并。
- 令 $i = p \to 2$,当前合并到 $2^{k_i}$ 和 $2^{k_{i-1}}$。可以观察到,$2^{k_{i-1}}$中一定有一个数与 $2^{k_i}$ 第一个数满足条件,所以将 $2^{k_{i-1}}$ 中那个数 `rotate` 到末尾即可。容易证明这样构造是对的。
- 称以这种方式构造出来的序列为 `CompactGrayCode`。
对于 $n \gt 1$ 时,分别构造 $n,m$ 所对应的 `CompactGrayCode`,记为 `CGCn` 和 `CGCm`。对于每个 $a_{i, j}$,都以二进制下的某种方式拼接 `CGCn[i]` 和 `CGCm[j]`,得到一组可行解。这样的正确性显然,问题也就变成了找到最小代价的拼接方式。
这里用 $n = m = 6$ 来加以说明。首先,`CGCn` 和 `CGCm` 均为:
$$5 = 101_{2}, 1 = 001_{2}, 3 = 011_{2}, 2 = 010_{2}, 0 = 000_{2}, 4 = 100_{2} $$
如果选择顺次拼接,那么矩阵如下图:
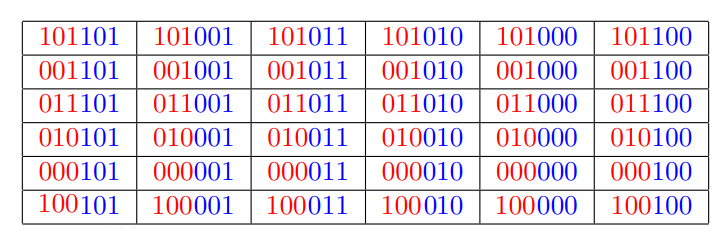
可以发现最大值为 $45 = \textcolor{red}{101}\textcolor{blue}{101}_2$。
但如果以下图拼接,
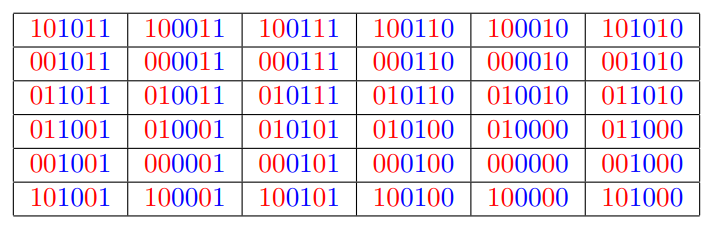
最大值仅为 $43 = \textcolor{red}{10}\textcolor{blue}{10}\textcolor{red}1\textcolor{blue}{1}_2
发现最大值只跟 CGCn 和 CGCm 中的最大值有关,于是可以 dp 求解。
`dp` 后构造方案是容易的。
参考实现:
```cpp
#include <bits/stdc++.h>
signed main () {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, m;
std::cin >> n >> m;
std::vector<std::vector<int>> Gray(11);
for (int i = 0; i <= 10; ++i) {
for (int j = 0; j < (1 << i); ++j) {
Gray[i].emplace_back(j ^ (j >> 1));
}
}
auto GetCompactGray = [&](int x) {
std::vector<std::vector<int>> tmp;
for (int i = 10; ~i; --i) {
if (x >> i & 1) {
tmp.emplace_back(Gray[i]);
}
}
int lim = 0;
for (auto &i : tmp) {
for (auto &j : i) {
j += lim;
}
lim += i.size();
}
for (int i = (int)tmp.size() - 1; i; --i) {
auto &l = tmp[i - 1], &r = tmp[i];
for (int j = 0; j < (int)l.size(); ++j) {
if (__builtin_popcount((l[j] ^ r[0])) == 1) {
rotate(l.begin(), l.begin() + j + 1, l.end());
break;
}
}
}
std::vector<int> res;
for (auto &i : tmp) {
res.insert(res.end(), i.begin(), i.end());
}
return res;
};
auto CompactGrayn = GetCompactGray(n--), CompactGraym = GetCompactGray(m--);
int x = (!n) ? 1 : std::__lg(n) + 1, y = (!m) ? 1 : std::__lg(m) + 1, all = x + y - 1;
std::vector<std::vector<int>> f(x + 1, std::vector<int>(y + 1, (1 << 11))), pre(f);
f[0][0] = 0;
for (int i = 1; i <= x; ++i) {
f[i][0] = f[i - 1][0] | ((n >> (x - i) & 1) << (all - i + 1));
pre[i][0] = 1;
}
for (int i = 1; i <= y; ++i) {
f[0][i] = f[0][i - 1] | ((m >> (y - i) & 1) << (all - i + 1));
pre[0][i] = 2;
}
for (int i = 1; i <= x; ++i) {
for (int j = 1; j <= y; ++j) {
int I = f[i - 1][j] | ((n >> (x - i) & 1) << (all - i - j + 1)), J = f[i][j - 1] | ((m >> (y - j) & 1) << (all - i - j + 1));
if (I < J) {
f[i][j] = I;
pre[i][j] = 1;
} else {
f[i][j] = J;
pre[i][j] = 2;
}
}
}
std::vector<int> from(x + y);
int now = 0;
for (; x || y; ) {
from[now++] = pre[x][y];
if (pre[x][y] == 1) {
--x;
} else {
--y;
}
}
for (int i = 0; i <= n; ++i) {
for (int j = 0; j <= m; ++j) {
//merge CompactGrayn[i] and CompactGraym[j]
int res = 0, x = CompactGrayn[i], y = CompactGraym[j];
for (int k = 0; k < now; ++k) {
if (from[k] == 1) {
res |= (x & 1) << k;
x >>= 1;
} else {
res |= (y & 1) << k;
y >>= 1;
}
}
std::cout << res << " \n"[j == m];
}
}
}
```