浅谈树状数组
Otachi
·
·
算法·理论
前置知识
:::info[为什么 $\operatorname{lowbit}$ 是这样计算的?]
因为计算机里用的是补码,所以将 $x$ 的所有二进制位取反后再加 $1$ 就可以得到 $-x$ 的二进制编码。设原先 $x$ 的二进制编码为 $(A10\cdots0)$,取反再加 $1$ 后得到 $-x$ 的二进制编码为 $(B10\cdots0)$。$A$ 和 $B$ 的每一位都是相反的,所以按位与之后只会保留 $(10\cdots0)$ 的部分,这就是我们想要的答案。
:::
# 一维树状数组
## 算法介绍
树状数组是一种支持**单点修改和区间查询**的数据结构,支持的操作需要满足**结合律和可差分性**。
:::info[什么是结合律和可差分性?]
结合律:满足 $(x\operatorname{op}y)\operatorname{op}z=x\operatorname{op}(y\operatorname{op}z)$ 的运算。
可差分性:满足已知 $(x\operatorname{op}y)$ 和 $x$ 可以求出 $y$ 的运算。
:::
先来看一道例题:[P3374 【模板】树状数组 1](https://www.luogu.com.cn/problem/P3374)
很容易想到 $O(nm)$ 的暴力,即遍历数组求和。但是这样显然是不行的,我们需要优化。
有人可能会想到这样优化:每次合并两个区间的和,方便计算。以样例为例,如下图所示:
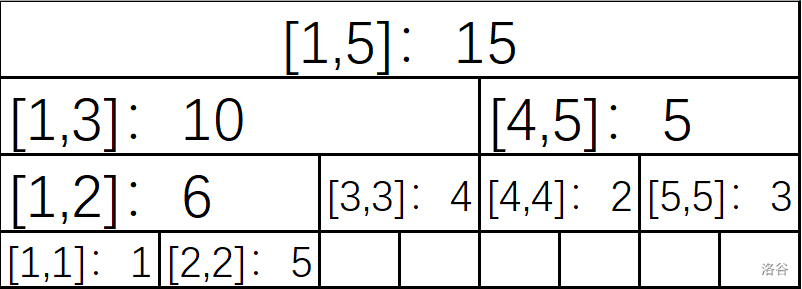
有人会说:主播主播你是不是放错图了这是线段树啊!
不好意思树状数组其实是线段树去掉无用状态后的产物,而这也是树状数组维护信息少的原因。
我们只考虑维护前缀和,这样区间和也可以通过前缀和的思想算出来。有些区间是无用的,如下图所示:
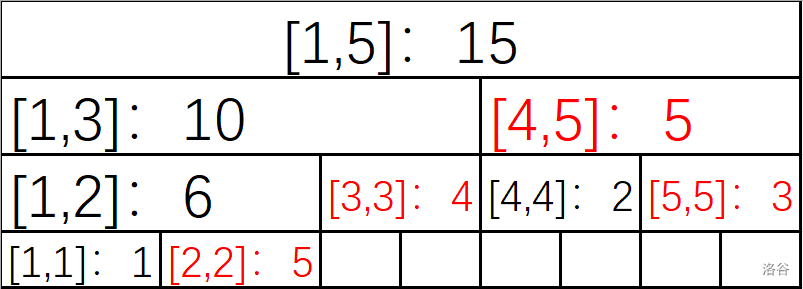
可以发现,标红的区间在维护前缀和的时候是没用的,于是我们可以给它去掉:
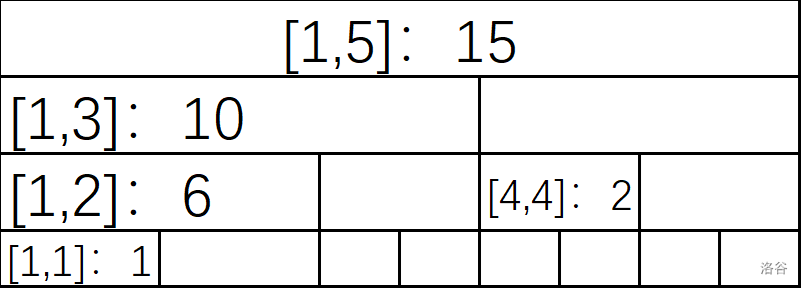
这个时候如果要修改,只需要不断向上传递就行了;如果要求和,只需要把对应的区间相加即可。那么怎么知道对应的是那些区间呢?这个时候就需要 $\operatorname{lowbit}$ 函数了。令
$$
tree_i=\sum_{j=i-\operatorname{lowbit}(i)+1}^{i}a_j
$$
### 区间查询
对于样例的数组,看一下树状数组是怎么处理查询操作的(这里假设没有进行任何操作,要处理 $[1,4]$ 的前缀和):
1. 先找到 $tree_4$,$tree_4$ 处理的区间是 $[4,4]$,加上 $2$。
2. 接下来要找 $[1,3]$ 的前缀和,找到 $tree_3$,$tree_3$ 处理的区间是 $[1,3]$,加上 $9$。
3. 区间覆盖完了,最终的和是 $12$。
通过刚才的模拟可以发现,如果要求 $[1,x]$ 的和,先找到 $tree_x$ 并加上,因为接下来要找 $[1,x-\operatorname{lowbit}(x)]$ 的和,所以再找到上一个区间 $tree_{x-\operatorname{lowbit}(x)}$,重复上面的操作。若 $x<1$ 说明区间覆盖完了。
### 单点修改
对于样例,看一下树状数组是怎么处理修改操作的(假设要对第 $3$ 个数加 $114514$)
1. 先找到 $tree_3$,加上 $114514$。
2. $tree_3$ 的上级是 $tree_5$,加上 $114514$。
3. 加完了,结束。
通过刚才的模拟可以发现,如果要把 $x$ 加上 $k$,先找到 $tree_x$ 并加上 $k$,因为 $x$ 的上级是 $x+\operatorname{lowbit}(x)$,所以再找上级 $tree_{x+\operatorname{lowbit}(x)}$,重复上面的操作,若 $x>n$ 说明所有的都已经加上了。
肯定会有人问:怎么建树呢?这个很简单,对于任意的 $i$,可以看作是对原本的 $0$ 加了 $a_i$。
### 代码实现
给出代码:
```cpp line-numbers
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=5e5+5;
int n,m;
ll tree[N];
inline int lowbit(int x)
{
return x&(-x);
}
void add(int x,int k)
{
while(x<=n)
{
tree[x]+=k;
x+=lowbit(x);
}
}
ll query(int x)
{
ll ret=0;
while(x>=1)
{
ret+=tree[x];
x-=lowbit(x);
}
return ret;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
ll x;
scanf("%lld",&x);
add(i,x);
}
while(m--)
{
int op;
scanf("%d",&op);
if(op==1)
{
int x;
ll k;
scanf("%d%lld",&x,&k);
add(x,k);
}
else
{
int x,y;
scanf("%d%d",&x,&y);
printf("%lld\n",query(y)-query(x-1));
}
}
return 0;
}
```
## 区间修改单点查询
例题:[P3368 【模板】树状数组 2](https://www.luogu.com.cn/problem/P3368)
看到区间修改单点查询就要想到差分,但是差分的瓶颈在于循环求和,于是可以考虑用一个树状数组维护差分数组。
给出代码:
```cpp line-numbers
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=5e5+5;
int n,m;
ll a[N],tree[N];
inline int lowbit(int x)
{
return x&(-x);
}
void add(int x,int k)
{
while(x<=n)
{
tree[x]+=k;
x+=lowbit(x);
}
}
ll query(int x)
{
ll ret=0;
while(x>=1)
{
ret+=tree[x];
x-=lowbit(x);
}
return ret;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
add(i,a[i]-a[i-1]);
}
while(m--)
{
int op;
scanf("%d",&op);
if(op==1)
{
int x,y;
ll k;
scanf("%d%d%lld",&x,&y,&k);
add(x,k);
add(y+1,-k);
}
else
{
int x;
scanf("%d",&x);
printf("%lld\n",query(x));
}
}
return 0;
}
```
## 区间修改区间查询
例题:[P3372 【模板】线段树 1](https://www.luogu.com.cn/problem/P3372)
:::warning[注意事项]{open}
因为这样需要两个树状数组,比较麻烦,所以还是建议老老实实打一个线段树。(不过实测发现似乎树状数组还是比线段树快)
:::
这道题可以理解为上一道题的 Pro Max 版,但是单点查询变成了区间查询。
我们依旧考虑前缀和并使用差分。化简一下式子:
$$
\sum_{i=1}^{x}a_i=d_1+(d_1+d_2)+\cdots+(d_1+d_2+\cdots +d_n)\\
=x\times d_1+(x-1)\times d_2+\cdots+[x-(x-1)]\times d_n\\
=x\times \sum_{i=1}^{x}d_i-\sum_{i=1}^{x}[(i-1)\times d_i]
$$
于是我们只需要建立两个树状数组,分别维护 $d_i$ 和 $(i-1)\times d_i$ 就行了。
给出代码:
```cpp line-numbers
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=5e5+5;
int n,m;
ll a[N];
ll tree1[N],tree2[N];
inline int lowbit(int x)
{
return x&(-x);
}
void add1(int x,ll k)
{
while(x<=n)
{
tree1[x]+=k;
x+=lowbit(x);
}
}
void add2(int x,ll k)
{
while(x<=n)
{
tree2[x]+=k;
x+=lowbit(x);
}
}
ll query1(int x)
{
ll ret=0;
while(x>=1)
{
ret+=tree1[x];
x-=lowbit(x);
}
return ret;
}
ll query2(int x)
{
ll ret=0;
while(x>=1)
{
ret+=tree2[x];
x-=lowbit(x);
}
return ret;
}
ll query(int x)
{
return x*query1(x)-query2(x);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
add1(i,a[i]-a[i-1]);
add2(i,(i-1)*(a[i]-a[i-1]));
}
while(m--)
{
int op;
scanf("%d",&op);
if(op==1)
{
int x,y;
ll k;
scanf("%d%d%lld",&x,&y,&k);
add1(x,k);
add1(y+1,-k);
add2(x,(x-1)*k);
add2(y+1,-y*k);
}
else
{
int x,y;
scanf("%d%d",&x,&y);
printf("%lld\n",query(y)-query(x-1));
}
}
return 0;
}
```
## 其他应用
### 求逆序对
个人感觉不如归并排序。
### 优化 dp
最典型的就是求 LIS。个人感觉不如贪心+二分。不过在很多时候还是很有用的。
# 二维树状数组
:::info[注意事项]{open}
这个基本不考,可以仅作了解。
:::
## 算法介绍
先来看一道例题:[P4514 上帝造题的七分钟](https://www.luogu.com.cn/problem/P4514)
~~UKE 大神好闪,膜拜 UKE!这道题目的题号怎么如此臭名昭著!~~
说句闲话:研究二维树状数组最好的方法是:A 了这道题,祝你们成功(滑稽
好了回归正题。很显然这需要维护一个**区间修改和区间查询**的树状数组。我们模仿一维树状数组,令
$$
tree_{i,j}=\sum_{x=i-\operatorname{lowbit}(i)+1}^{i}\sum_{y=j-\operatorname{lowbit}(j)+1}^{j}a_{x,y}
$$
还是考虑二维差分,关于二维差分可以见[这篇文章](https://www.luogu.com.cn/article/bdujxa8b)。
化简一下式子:
$$
\sum_{i=1}^{n}\sum_{j=1}^{m}a_{i,j}=\sum_{i=1}^{n}\sum_{j=1}^{m}\sum_{x=1}^{i}\sum_{y=1}^{j}d_{x,y}
$$
现在看起来可能比较丑陋,但是观察可得,$d_{1,1}$ 出现了 $x\times y$ 次,$d_{1,2}$ 出现了 $x\times(y-1)$ 次……以此类推,$d_{i,j}$ 出现了 $(n-i+1)\times(m-j+1)$ 次,于是可以把式子化简为:
$$
\sum_{i=1}^{n}\sum_{j=1}^{m}a_{i,j}=\sum_{i=1}^{n}\sum_{j=1}^{m}\sum_{x=1}^{i}\sum_{y=1}^{j}d_{x,y}\\
=\sum_{i=1}^{n}\sum_{j=1}^{m}[d_{i,j}\times(n-i+1)\times(m-j+1)]\\
=(n+1)\times(m+1)\times\sum_{i=1}^{n}\sum_{j=1}^{m}d_{i,j}-(m+1)\times\sum_{i=1}^{n}\sum_{j=1}^{m}(d_{i,j}\times i)-(n+1)\times\sum_{i=1}^{n}\sum_{j=1}^{m}(d_{i,j}\times j)+\sum_{i=1}^{n}\sum_{j=1}^{m}(d_{i,j}\times i\times j)
$$
于是我们只需要建立四个树状数组,分别维护 $d_{i,j},d_{i,j}\times i,d_{i,j}\times j,d_{i,j}\times i \times j$ 就行了。为了方便,这里我用了结构体。
给出代码:
```cpp line-numbers
#include<iostream>
using namespace std;
const int N=2050;
int n,m;
char op;
int a,b,c,d,k;
inline int lowbit(int x)
{
return x&(-x);
}
struct BIT
{
int tree[N][N];
void add(int x,int y,int k)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=n;j+=lowbit(j))
tree[i][j]+=k;
}
int query(int x,int y)
{
int ret=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
ret+=tree[i][j];
return ret;
}
}tree1,tree2,tree3,tree4;
void _add_(int x,int y,int k)
{
tree1.add(x,y,k);
tree2.add(x,y,k*x);
tree3.add(x,y,k*y);
tree4.add(x,y,k*x*y);
}
int _query_(int x,int y)
{
return (x+1)*(y+1)*tree1.query(x,y)-(y+1)*tree2.query(x,y)-(x+1)*tree3.query(x,y)+tree4.query(x,y);
}
int main()
{
cin>>op>>n>>m;
while(cin>>op)
{
if(op=='L')
{
cin>>a>>b>>c>>d>>k;
_add_(a,b,k);
_add_(a,d+1,-k);
_add_(c+1,b,-k);
_add_(c+1,d+1,k);
}
else if(op=='k')
{
cin>>a>>b>>c>>d;
cout<<_query_(c,d)-_query_(c,b-1)-_query_(a-1,d)+_query_(a-1,b-1)<<endl;
}
}
return 0;
}
```
# 总结
树状数组的优势是:码量少,常数小;劣势是:可维护信息较少。但也不失为一种优秀的数据结构。