圆方树学习笔记 —— 一种关于点双连通分量的思考方式
XuYueming
·
2025-07-19 20:50:46
·
算法·理论
洛谷不支持折叠块、HTML 标签,在此仅做简单删除 ,因此不得不去除折叠块包裹的代码,也因此不能通过超链接在文章内跳转,为了更好的阅读体验,强烈建议去我的博客阅读 。
引言
本文原名为《圆方树学习笔记 & 最短路题解》,原始版本可见文末。
本文旨在系统梳理 圆方树(Block forest) 及其思想在图论问题中的应用,尤其是在信息学奥林匹克竞赛(OI)中的实际价值。
我们将从一种特殊的图结构——仙人掌图(Cactus Graph)出发,逐步扩展至一般无向图,分析如何通过构造圆方树,来将复杂图上问题转化为树上问题,并借助经典算法(如树形 DP、树链剖分、DDP、虚树等)解决。
本文对涉及的问题进行了系统归类,并配有例题与代码,构建出一套完整的知识体系,帮助读者深入理解核心思想并掌握其在实际题目中的变形与拓展。当然,并非所有问题都需要显式构造圆方树,部分情况下我们仅借助其结构思想进行分析和维护。
在此基础上,本文还创新性地提出了「圆树」这一辅助结构的概念,以优化特定类型问题的建模与求解过程。
希望本笔记能为正在学习相关内容的读者提供一套完整、实用的参考资料。
全文约二十万字符,除代码外有五万字,因此建议阅读的同时做题来巩固知识。
问题引入
在处理无向图上的复杂问题时,我们常借助图的结构性质进行化简,在简化后的图上使用算法解决问题。比如,使用 Tarjan 算法对图进行缩点:
强连通分量 缩点后可构成一个有向无环图(DAG) ;边双连通分量 缩点后可转化为一棵树 ;那么,点双连通分量 缩点之后,会变成什么结构?
答案是:圆方树(Block forest) 。
圆方树正是对图进行点双连通分量 缩点后的结构表示。它将原图中复杂的连通关系映射为树上的结构,从而使许多原本难以处理的问题得以简化为树上问题 ,显著降低分析与求解的难度。
圆方树的定义
在一张无向图中,对每个点双连通分量建立一个对应的超级节点 ,并将该分量中所有原图中的点与该超级节点相连,随后删除原图中的所有边。在构建完成后:
将这些新增的超级节点称为 「方点」 ;
将原图中的普通节点称为 「圆点」 ;
这样得到的一棵圆点与方点交错连接的树结构 ,即为该图的圆方树。
在圆方树上,一个方点的父亲一定是圆点,我们称这个圆点为它的 「父亲圆点」 ,类似定义 「孩子圆点」 ,对于一个圆点类似定义 「父亲方点」 ,「孩子方点」 。
以下展示的是一张无向图及其对应的圆方树结构。例如,原图中点双 \{2,3,4,5\} 对应超级节点 15 ,在圆方树中,15 和 2,3,4,5 都连有边。
本文中,若无特殊说明,认为「两点被一条边连接」这种图结构 是一个点双 ,如上图中 \{8,9\} 。并为这种点双同样创建一个方点。即在圆方树上不会出现两个圆点直接相连的情况,即不出现圆圆边 。
圆方树的简单性质
我们首先需要对圆方树的基本特点有一定了解。
圆方树节点数小于 2n ,其中 n 为原图点数。
一个点双引入一个方点,一张图的点双最多只有 n-1 个,这个上界在图退化为树的情况下达到。所以代码中不要忘记给相关数组开两倍大小。
圆方树上一种类型的点只会和另一种类型的点连边。
方点只会和圆点连边,圆点只会和方点连边。由定义不难得到这一点。
圆方树上任意一条树链都是「圆方交错」的。
结合上一条性质,不难发现这个性质。
圆方树构建方式
一种简洁而典型的圆方树建树方法是:在运行 Tarjan 算法求点双连通分量的同时构造圆方树 。并且可以直接把圆方树建成一棵外向树 ,便于后续树上遍历。我们直接让方点从 n+1 开始编号,圆点保持原图上的编号。
见博客。
这是最基础的构建框架,在后文具体问题中,我们将在此代码的基础上进行拓展,比如,为圆方树赋上边权,维护当前点双的子图。
圆方树维护点对间所有简单路径信息
关于原图中两点 u,v 之间所有的简单路径,我们可以将其映射到圆方树上 u,v 之间的树链,并且借助圆方树的树形结构,来维护这些所有简单路径的信息和。
点对间所有简单路径信息
对于圆方树的映射方式,等到我们分析完信息维护的方式,就呼之欲出了。
我们先来看几种典型的信息:u,v 间最长简单路径长度、u,v 间简单路径条数、u,v 间所有简单路径长度之和、所有能被某一条 u,v 间简单路径经过的点权和。
我们可以大致分为如下两类。
类型一:满足分配率的边权、点权相关信息
让我们尝试用形式化的语言来形容,进行适当抽象。
设 p_i(u,v) 表示某一条 u\rightarrow v 的简单路径。对于这一条简单路径的信息,如果可以看做其中每一条边 e\in p_i(u,v) 的信息 \operatorname{info}(e) 按照一种特定的合并方式 \odot 合并后的结果,我们就称这种信息为 「边权相关信息」 ,即路径 p_i(u,v) 的信息为 \operatorname{info}(p_i(u,v)) = \bigodot\limits_{e\in p_i(u,v)}\operatorname{info}(e) 。类似定义点权相关信息,处理这种信息,可以把所有点的点权按照一种方式变成边权,除了某一点需要特殊考虑,剩下维护的就是边权相关信息。因此为了简化讨论,仅考虑边权相关信息。例如:「路径长」是边权相关信息,对于一条边 e ,\operatorname{info}(e) 就是 e 的长度 \operatorname{len}(e) ,\odot 即为 + ,\operatorname{info}(p_i(u,v)) = \bigodot\limits_{e\in p_i(u,v)}\operatorname{info}(e) = \sum\limits_{e\in p_i(u,v)}\operatorname{len}(e) 。
所求的是对于 u,v 间所有简单路径的信息,按照 \oplus 合并后的结果,即 \operatorname{info}(u,v)=\bigoplus_i\operatorname{info}(p_i(u,v)) 。\oplus 显然需要满足交换律,否则答案就不唯一了。例如,对于「最长简单路径长度」,就是「路径长」通过 \max 合并后的信息,\odot=+ ,\oplus=\max ,\operatorname{info}(u,v)=\max_i\operatorname{info}(p_i(u,v))=\max_i\sum\limits_{e\in p_i(u,v)}\operatorname{len}(e) 。
明确需要求解什么后,考虑如何维护。
考虑什么情况下可能可以合并 \operatorname{info}(u,v) 与 \operatorname{info}(v,w) 得到 \operatorname{info}(u,w) 。发现当且仅当 v 是割点的时候,合并信息,才可能得到不重不漏的的结果。因为 v 作为割点,u\rightarrow w 的每一条简单路径总是可以拆分成 u\rightarrow v 和 v\rightarrow w 两条仅在 v 处相交的简单路径。这是类似于卷积的,即对于所有 i,j ,p_i(u,v)\sim p_j(v,w) 拼出了一条 p_k(u,w) ,并且这种 i,j\mapsto k 的映射是唯一的。那么 \operatorname{info}(u,w)=\bigoplus_k\operatorname{info}(p_k(u,w))=\bigoplus_{i,j}\operatorname{info}(p_i(u,v)\sim p_j(v,w)) 。
在树上,因为 u\rightarrow v 和 v\rightarrow w 的简单路径是唯一的,我们有 \operatorname{info}(u,w)=\operatorname{info}(u,v)\oplus\operatorname{info}(v,w) ,这是简单的。但是此时 u\rightarrow v 和 v\rightarrow w 的简单路径不是唯一的,就不能直接通过 \oplus 合并了。
有时候我们能够找到一种运算 \otimes ,使得我们可以打开这个 \bigoplus ,直接合并两个子问题的信息。它需要满足 \bigoplus_{i,j}\operatorname{info}(p_i(u,v)\sim p_j(v,w))=\Big(\bigoplus_{i}\operatorname{info}(p_i(u,v))\Big)\otimes\Big(\bigoplus_{j}\operatorname{info}(p_j(v,w))\Big) ,也就是通过 \otimes 类似树上直接合并两个子问题的信息。把 \operatorname{info} 用 \odot 表示,也就是 \bigoplus_{i,j}\bigodot_{e\in p_i(u,v)\sim p_j(v,w)}\operatorname{info}(e)=\Big(\bigoplus_{i}\bigodot_{e\in p_i(u,v)}\operatorname{info}(e)\Big)\otimes\Big(\bigoplus_{j}\bigodot_{e\in p_j(v,w)}\operatorname{info}(e)\Big) 。为了方便观察,不妨用 S_i 表示 p_i(u,v) ,T_i 表示 p_i(v,w) ,等式变为:\bigoplus_{i,j}\bigodot_{e\in S_i\cup T_j}\operatorname{info}(e)=\Big(\bigoplus_{i}\bigodot_{e\in S_i}\operatorname{info}(e)\Big)\otimes\Big(\bigoplus_{j}\bigodot_{e\in T_j}\operatorname{info}(e)\Big) 。用 f_i 表示 \bigodot_{e\in S_i}\operatorname{info}(e) ,g_j 表示 \bigoplus_{j}\bigodot_{e\in T_j}\operatorname{info}(e) ,上等式变成:\bigoplus_{i,j}\Big(f_i\odot g_j\Big)=\Big(\bigoplus_{i}f_i\Big)\otimes\Big(\bigoplus_{j}g_j\Big) 。这个形式很像分配律,进一步,我们可以断言,当且仅当 \odot 对 \oplus 满足 分配律 时,\otimes 存在,且 \otimes 就是 \odot 本身,此时,\odot 和 \oplus 构成一个 半环 。
例如,当 \odot=+ ,\oplus=\max 时,+ 对 \max 满足分配律,此时 \otimes 存在,且 \otimes=\odot=+ 。实际图论意义也很好理解,u\rightarrow w 所有简单路径中的最长的长度,即为 u\rightarrow v 和 v\rightarrow w 分别找到两条最长的拼起来。当 \odot=\times ,\oplus=+ 时,\times 对 + 满足分配律,此时 \otimes 存在,且 \otimes=\odot=\times 。当 \odot=\oplus=+ 时,+ 对 + 不满足分配律,我们找不到 \otimes 这个运算吗?若仅记录「边权相关信息」,我们确实找不到这样一个运算。但是在后文,我们通过扩展信息的方式,找到了维护这种信息的方式。
有了合并信息的方式,我们要考虑 「原子信息」 ,即小到不能再小的信息,此时就是 u,w 处在同一个点双的时候,我们不能找到一条连接 u,w 的简单路径通过某一个割点 v ,于是不能通过合并信息的方式得到 u\rightarrow w 的信息。不妨对于处于同一点双中的 u,w ,用 \operatorname{info}(u,w) 表示 u,w 之间的原子信息。原子信息通常是能够方便处理出来的。
我们已经学会了如何维护 \odot 对 \oplus 满足分配律的「边权相关信息」、「点权相关信息」。
类型二:非权值相关信息或 \odot=\oplus 的权值相关信息
此时只存在 \otimes 这个合并运算。预处理出原子信息同样通常是简单的。例如对于「简单路径条数」,\otimes 就是 \times 。
上文中遗留一个问题,当 \odot=\oplus=+ 时,由于 + 对其自身不具有分配律时,不能直接通过「边权相关信息」的方式维护。考虑扩展信息,设 \operatorname{info}(u,v)=(s,c) ,其中 s 表示所求的「所有简单路径长度之和」,c 表示 u\rightarrow v 简单路径条数。我们惊喜地发现,有 (s_1,c_1)\otimes(s_2,c_2)=(s_1c_2+s_2c_1,c_1\cdot c_2) ,这是可以维护的!式子的意义是,对于每一条 p_i(u,v) ,由于有 c_2 条 p_j(v,w) ,所以 s_1 会贡献 c_2 次。
推广到到一般情况,当 \odot=\oplus 且对自身不具有分配律时,由于 \oplus 具有交换律,那么 \odot 也具有交换律,我们总是可以多记录一个 c ,有 (s_1,c_1)\otimes(s_2,c_2)=\Big((\odot_{c_2}(s_1))\odot(\odot_{c_1}(s_2)),c_1\cdot c_2\Big) ,其中 \odot_{k}(x)=\underbrace{x\odot x\odot\cdots\odot x}_{k\text{ 个 }x} 。
还有另一种可能需要维护的信息,即求能被任意一条 u\rightarrow v 简单路径经过的所有点 / 边的权值和,这个问题其实非常好处理,只需令 \otimes=\oplus 即可,这样就能统计到所有点 / 边的权值和,这和树上十分类似。
总结
以上几种信息,在处理完原子信息后,最后都是需要在一个个割点处,将信息通过 \otimes 合并起来,这正是圆方树可以解决的。
支持查询信息
让我们回到圆方树上,看看它对我们维护信息有什么帮助。
对于 u\rightarrow v 路径上的信息,可以将路径拆分成不断从一个点双走到另一个点双的过程,即 w_1 \stackrel{d_1}{\longrightarrow} w_2\stackrel{d_2}{\longrightarrow} w_3\stackrel{\cdots}{\longrightarrow} w_{m-1}\stackrel{d_{m-1}}{\longrightarrow}w_m ,其中 w_1=u, w_m=v ,对于 i=1,\ldots,m-1 ,w_{i},w_{i+1} 分别是编号为 d_i 的点双中两个点。根据上述讨论,我们要求的就是 \bigotimes\limits_{i=1}^{m-1}\operatorname{info}(w_i,w_{i+1}) ,而每个 \operatorname{info}(w_i,w_{i+1}) 均为原子信息。
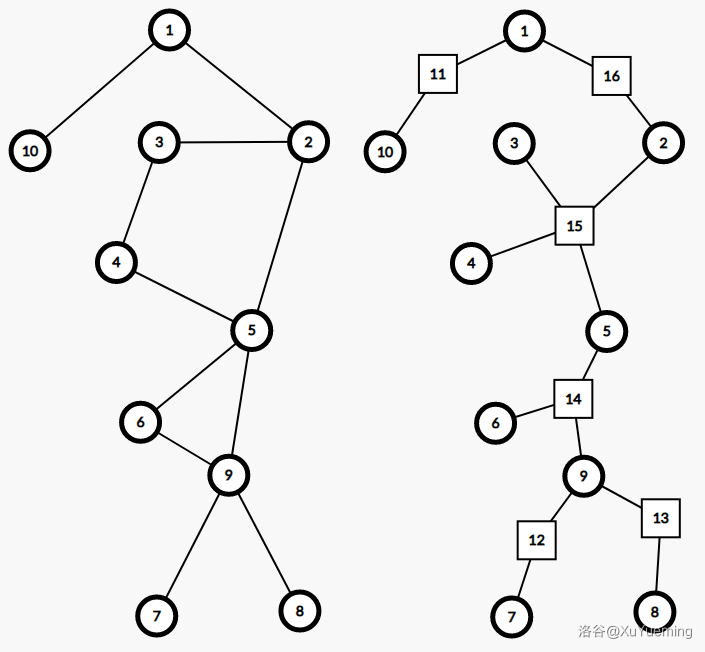
1. 圆方树上一条「圆方圆」的路径,对应原图点双中两点之间所有简单路径。
比如上图中 $\{3,15,5\}$ 这条圆方圆路径,对应原图中 $\{2,3,4,5\}$ 这个点双中以 $3,5$ 为端点的所有简单路径,即 $\{3,2,5\},\{3,4,5\}$ 两条简单路径。
这就是进入一个点双,再从这个点双中走出来。
1. 圆方树上任意一条树链 $(u,v)$ 对应原无向图中 $u,v$ 之间所有简单路径。
比如上图中 $(3,8)$ 这条树链,对应了原图中 $\{3,2,5,9,8\},\{3,2,5,6,9,8\},\{3,4,5,9,8\},\{3,4,5,6,9,8\}$ 这些简单路径。
这种把每一条「圆方圆」的路径合并起来的过程,对应不断从一个点双走到另一个点双的过程。
圆方树很好地刻画了通过 $\otimes$ 合并信息的过程!让我们继续分析。
对于一次查询 $(u,v)$,设 $p=\operatorname{lca}(u,v)$,将树链拆分成 $u\rightarrow p\rightarrow v$。考虑 $u\rightarrow p$ 一侧,另一侧类似。
考虑如下圆方树一部分:
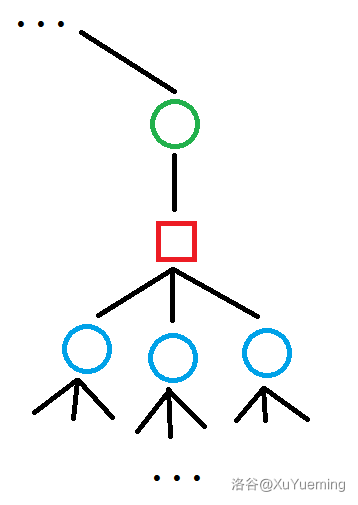
当我们经过某一个圆点(蓝点)$u$,跳向它爷爷(绿点)$v$ 时,需要求的是 $u$ 和 $v$ 的原子信息 $\operatorname{info}(u,v)$。不考虑修改的情况下,每一次从 $u$ 跳到 $v$,原子信息都是相同的,因为它的爷爷 $v$ 是唯一的。我们于是这可以预处理出这些原子信息,而这类原子信息的个数和非根圆点个数相同,是 $\mathcal{O}(n)$ 的。我们将 $u$ 和 $v$ 的信息,放在 $u$ 到它父亲方点(红点)的边权上,每个方点和它父亲圆点之间的边权设为单位元。那么我们考虑一对具有祖孙关系的节点,他们之间的信息,便是圆方树上他们之间边权按序合并的结果。
对于 $u\rightarrow p$ 和 $p\rightarrow v$ 两段,根据我们赋的边权,和我们之前学过的树上信息维护方式,这两段路径的信息已经可以求出。对于不满足交换律的信息,可能需要维护向上跳的信息和向下跳的信息。接下来,好像直接把这两个信息合并起来就是对的,其实不然。对于 $p$ 是圆点的情况,这么做是正确的;但是对于 $p$ 是方点的情况,设 $u'$ 为 $p$ 的孩子且是 $u$ 的祖先,$v'$ 同理,那么考虑直接合并信息的实际意义,是从 $u$ 走到 $u'$,进入了 $p$ 对应的点双,走到了 $\operatorname{fa}(p)$,再走进 $p$ 对应的点双,走到 $v'$,最终到 $v$。这显然是错误的,我们要求 $u'\rightarrow v'$ 的原子信息 $\operatorname{info}(u',v')$,而非 $\operatorname{info}(u',\operatorname{fa}(p))\otimes\operatorname{info}(\operatorname{fa}(p),v')$。解决方式很简单,只需要特殊查询一次 $u'\rightarrow v'$ 的原子信息,和之前两个信息合并。
在实现上,我们需要支持询问点双内两点之间的原子信息,那么这是否意味着需要为每个点记录其所在所有点双内的信息?如果真的需要,我们可以为每一个元素开 $m+1$ 个 `vector`,其中 $m$ 个 `vector<> info` 用来记录信息,$1$ 个 `vector<int> id` 用来存所有 $u$ 点双的编号,意为 $u$ 在编号为 `id[u][i]` 的点双内对应的信息为 `info[u][i]`,对于查询 $u$ 在编号为 $x$ 的点双中的信息,先在 `id[u]` 中二分出 $x$ 的下标,再拿这个下标去访问 `info[u]`。但是这是不必要的,这是因为我们的查询并不真的「任意」,而是只会查询一个圆点,在其父亲方点对应点双中的信息。而每个孩子圆点的父亲是唯一的,如果他被查询到,所用到的信息也是唯一的,那就不需要使用 `vector` 了。`vector` 的写法请参考下文仙人掌部分[例五代码](#vectorInfo)。
至此,我们借助圆方树的特殊结构,结合树上信息维护方式,通过 $\otimes$ 的合并方式,可以查询给定点对间所有简单路径的信息。
### 支持修改信息
如果有了修改呢?树上我们使用树剖来支持修改查询树链信息,那么接下来要做的就是把圆方树剖开,尝试在上面维护信息。
先来考虑一种特殊的信息,求 $u\rightarrow v$ 能到达的所有点的点权的信息和。这时候同一个点双内 $u\rightarrow v$ 的信息为点双中除去 $v$ 的点权信息和。发现圆方树上的边权很有规律,对于一个方点,它连向所有孩子圆点的边权总是相同的,都是该点双中除去父亲圆点的点权信息和。我们把边权上放,给方点一个点权(注意和原点权加以区分),为原先我们给圆方树赋的边权,再把圆点的点权设置为单位元。我们的查询似乎就变成了圆方树上路径的点权信息之和。
考虑在 LCA 处的特殊情况。若 LCA 为方点,同样需要得到 $u'\rightarrow v'$ 的信息。如果严格遵循上文对原子信息的定义,我们需要先扣掉 $v'$ 的点权,但是这样到最后会漏掉 $v'$ 的点权(点权转换后的特殊情况),所以我们完全不必扣掉 $v'$ 的点权,而是查出 LCA 的点权后,再加上 LCA 父亲圆点的点权。对于 LCA 为圆点的情况,我们统计漏了这个 LCA 圆点的信息,这把它的点权贡献到答案里就好了。如此就完成了查询。
修改某个点的权值的时候,除了需要维护仙人掌上每个点的点权,还要修改其在圆方树上父亲方点的点权。要想快速得到新的点权,要对每一个方点维护一个支持插入删除的数据结构,每次先删除原先的贡献,再加入修改后点权的贡献即可。
我们现在只需要在一棵树上,支持修改点权,询问 $\operatorname{lca}$,询问路径点权和。这个可以树剖做到 $\log^2$,或者可以做到单 $\log$。另外,理论上来说,我们还可以继续上放点权,也就是在圆树操作。但是这会造成很多边界情况,不优雅,故不展开讨论。
考虑更为一般的情况。我们发现边权上放的本质是为了修改的时候,能够将父亲方点的所有孩子圆点往上跳的边权都修改。但是真的一定需要更新每个孩子圆点吗?并不是,我们只需要修改重孩子圆点。每次跳重链时,只需要考虑链顶这个轻儿子的特殊情况。于是完成了修改和维护信息。
## 「圆树」:不设置方点的可行性
上文中,方点的作用仅是用来判断 $u'$ 和 $v'$ 是否在同一点双内,在一些简单的问题中,我们确实可以不建出方点,只建出「圆树」,并在每个点记录它在圆方树上父亲方点是谁,在查询的时候,只需要要找出 $u',v'$(如果存在的话),然后判断他们的父亲圆点是否相同,就能知道 LCA 是方点还是圆点。
### 优点
1. 节点总数为 $n$:
不引入新的方点,整棵树的节点数量保持为原图大小的 $n$,在最坏情况下仅为传统圆方树节点数的一半。这样可以节省时间空间,而且不会因为手残数组开小,或者预处理只处理到 $n$ 而红温。
1. 实现简单:
若采用倍增算法来维护树上信息和求 LCA,当一个节点是另一个节点的祖先时,不会出现 LCA 是方点的特殊情况。剩下来的情况,我们倍增本来就是先求出了 $u',v'$,然后再跳最后一步到 LCA 的,那我们在跳之前判断一下就好了,不必等到跳了才发现是同一个方点。
### 缺点
1. ~~过度依赖倍增:~~
~~若题目采用树上前缀和、差分等方式来维护信息,通常使用基于 DFS 序的 $\mathcal{O}(1)$ LCA 算法,而寻找 $u', v'$ 却是 $\mathcal{O}(\log n)$ 的,导致效率不匹配。除非你愿意使用如长链剖分实现 $\mathcal{O}(1)$ 的 kth-father 查询:先求出 LCA,再通过深度差计算 $u'$ 或 $v'$,这会显著增加代码复杂度。~~
发明了基于 DFS 序 $\mathcal{O}(1)$ 求 $u',v'$ 的算法,可见:[博客](https://www.cnblogs.com/XuYueming/p/18919143)。
1. 在特定情况下有过多边界问题:
例如维护需要支持修改的信息,使用圆树将需要很多分类讨论,万一没有讨论所有情况,就会出错,而且代码将变得难以理解。
1. 过于小众:
~~求调的时候别人说看不懂~~。
------
总而言之,这是仅是一种小优化,在掌握了圆方树的基本构造与思想后,读者可根据题目类型与实现习惯,自行选择是否采用此优化版本。
圆树和圆方树两种写法,在[例题五](#exampleP5)和[例题十三](#exampleP13)均分别给出,供参考对比。
## 圆方树在「仙人掌」上的应用
我们先从 **仙人掌** 这种特殊的无向图开始研究圆方树,这是因为仙人掌具有十分良好的性质。
### 初识仙人掌
#### 仙人掌的定义
仙人掌指任意一条边最多出现在一个简单环中的无向连通图。
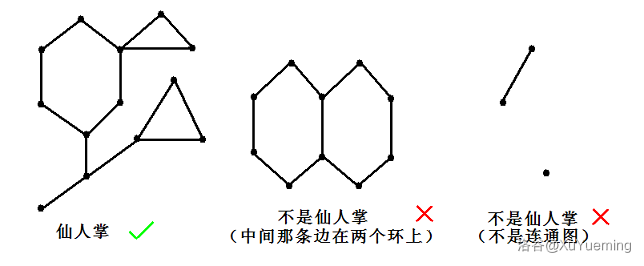
#### 仙人掌的性质
1. 仙人掌边数上界为 $\mathcal{O}(n)$。
准确来说,为 $2n-2$ 或 $\lfloor\frac{3}{2}(n-1)\rfloor$。
当允许重边时,把一棵树的所有 $n-1$ 条树边,复制一遍,得到一棵 $2n-2$ 条边的仙人掌。注意不可能出现三条重边连接两个点,否则就不满足仙人掌的定义了。
当不允许重边时,可以发现如下「类菊花」的结构使得边数达到最多,为 $\lfloor\frac{3}{2}(n-1)\rfloor$。
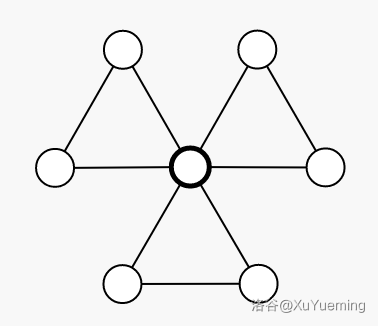
1. 仙人掌具有类似树的结构。
我们发现,由于仙人掌的环不交(准确的说为边不交),这使得其保留了树的一些形态。
把每一个环看做一个巨大的节点,仙人掌就成了一棵树了,只不过有些节点间不依靠边相连,而是在公共点处相切。
类似树上「子树」,我们可以定义「子仙人掌」。
**「子仙人掌」:**
指定一个根,定义 $u$ 的「子仙人掌」为,断开根和 $u$ 的所有简单路径的边后,$u$ 所在的连通块。
不难发现,$u$ 的「子仙人掌」对应圆方树上 $u$ 的子树。画个图就十分清晰了:
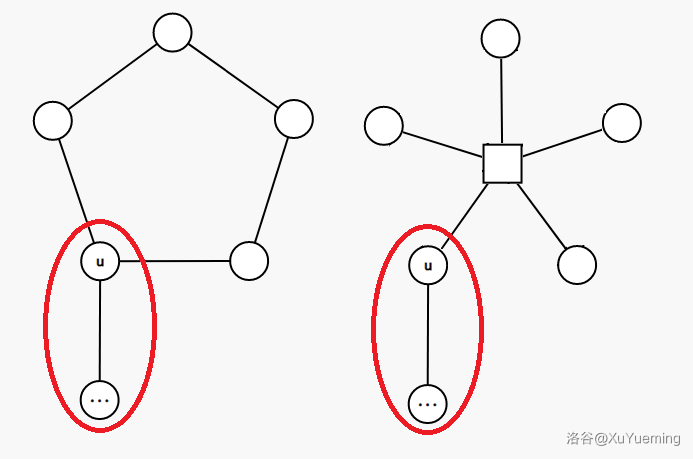
不难做进一步推广,类似在一般无向图上定义「子无向图」,容易发现,这同样对应圆方树的子树。
类似树上「树链」,在 **只存在奇环** 的仙人掌上,由于最长 / 短路唯一,我们可以定义「长链」、「短链」的概念。
**「长链」、「短链」:**
$u,v$ 之间经过边数最多的的简单路径称为 $u,v$ 间的「长链」;$u,v$ 之间经过边数最少的简单路径称为 $u,v$ 间的「短链」。
显然,在仙人掌中每经过一个环时,若都选择**在环上走最长(或最短)路径**,则整条走出的路径即为 $u, v$ 间的长链(或短链)。
需要注意仙人掌上的点双并 **不一定是环**,通过一条不在环上的边连接的两个点,构成了两个点的点双,而这个点双不是一个环。有时候我们需要特判这种情况。
### 仙人掌上构造圆方树
我们可能需要在构造圆方树的时候,维护当前环的形态,即得到当前环对应的子图。
#### 方法一:树上前缀和
一种做法是,对每个节点维护在 tarjan 的 dfs 树上的树上前缀和(即到根的信息),对于在 dfs 树上 $u$ 是 $v$ 的祖先,用 $v$ 的前缀和减去 $u$ 的前缀和,就能得到 $u$ 到 $v$ 之间的信息。那我们选用父亲圆点 $u$ 作为环首,这样环上每一个点都处于 dfs 树中 $u$ 的子树中,于是可以得到每个点到环首 $u$ 的信息。至于总环长,发现我们上述过程考虑的是一条以 $u$ 为环首的一条链,对于环尾 $v$,他有且仅有一条返祖边,且这条返祖边恰连向 $u$,从而构成一个环。一个点不可能有两条或以上返祖边,否则不满足仙人掌的定义。而这个返祖边我们可以轻松维护。如下图,蓝色的边为 dfs 树树边,红色的边为返祖边,细黑边为圆方树上的树边。当前的环即为若干条蓝边和一条红边构成的环。绿色箭头表示环首走向环尾的方向,蓝紫色箭头指向形成闭环的那条环尾指向环首的边。
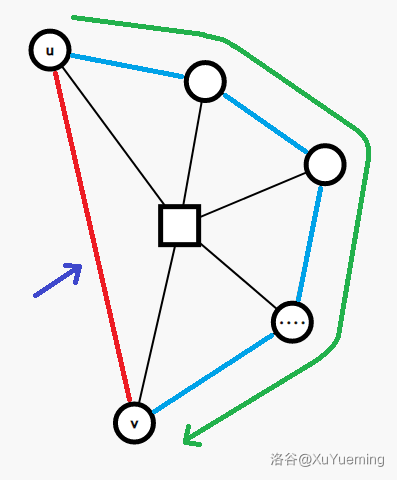
#### 方法二:弹边栈
这种做法对于不可差分信息不太好处理,并且依赖于环这种形态,不好向一般点双拓展。考虑类似点的栈,维护一个边的栈,存返祖边和树边,在 tarjan 的过程中,每次找到一个点双($\operatorname{low}(v) \geq \operatorname{dfn}(u)$),就不断弹栈,直到弹出连接 $u,v$ 的**树边**(注意必须是树边)。这个过程中弹出的边,便构成了这个点双的子图。对于复杂一些的点双,我们需要建出这个子图,然后在这个子图上跑一些算法,但是于仙人掌而言,我们把一个环建出来再处理,未免小题大做了。我们发现按照弹栈的顺序,弹出的边依次为环中的返祖边,深度最深的树边,深度次深的树边,直到 $u,v$ 之间的树边。更加优雅的做法是,我们按照弹栈的顺序,假设当前弹出的边为 $u'\rightarrow v'$,边权为 $w$,并且不是连接 $u,v$ 的树边,设 $u$ 在环上的信息前缀和为 $p_u$,那么就让 $p_{u'}\gets p_{v'}+w$。这种方法下,环首为 $u$,环尾是 $v$,$u,v$ 之间的树边成了环尾连向环首的边。如下图。事实上,使用了这种方式,我们不需要原先的点栈,每次弹出的边的起点,相当于原先点栈每次弹出的点。
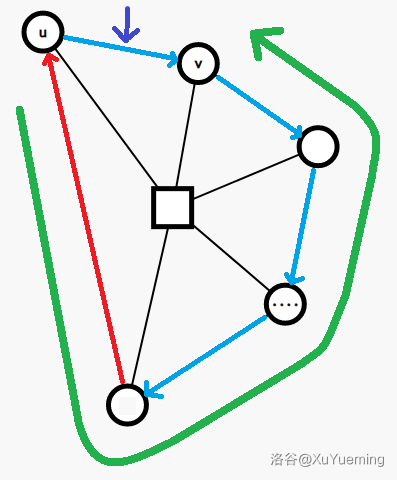
### 类型一:单次询问整体信息
#### 计数类问题
在处理计数类问题时,往往需要借助圆方树进行类似树形 DP,或其他类似树上的统计方法。
在普通树上,这类问题我们已非常熟悉;放到基环树上,常见的技巧是将环上 DP 与树形 DP 分开处理,其本质原因是,把环上每个结点看做对应树根,这棵树是一个子问题,所以剩下的部分是一个环上问题。
在仙人掌上,由于我们前文提到的仙人掌具有的类似树的性质,所以在 DP 转移的时候,可以分环上 DP 和树形 DP 进行转移,或者按照环上和树上进行统计答案。这在圆方树上体现为,在方点、圆点上分别处理。
实际上,对于这类问题,我们甚至无需显式构建整棵圆方树。只需在分析与转移过程中设想当前所处的是圆点还是方点,并据此决定转移逻辑,即可完成建模与求解。这也是圆方树思想灵活而强大的体现。
**例一、静态仙人掌最大独立集(小 C 的独立集,link、link、link):**
**Problem Statement:**
给你一个有 $n$ 个点和 $m$ 条边的仙人掌,求它的最大独立集大小。
$n\leq 5\times 10^4$,$m\leq 6\times 10^4$。
**Problem Analysis:**
树上最大独立集是经典的(猜你想找:[没有上司的舞会](https://www.luogu.com.cn/problem/P1352)),我们设 $f_{u,0/1}$ 表示以 $u$ 为根的子树这个子问题,$u$ 选 / 不选,最大独立集为多少。转移为 $f_{u,0}=\sum\limits_{v\in\operatorname{son}(u)}\max\Big\{f_{v,0},f_{v,1}\Big\}$,$f_{u,1}=\operatorname{val}(u)+\sum\limits_{v\in\operatorname{son}(u)}f_{v,0}$。
基环树上最大独立集是经典的(猜你想找:[MAFIJA](https://www.luogu.com.cn/problem/P6417),[\[ZJOI2008\] 骑士](https://www.luogu.com.cn/problem/P2607)),我们先把树形 DP 跑了,得到环上每个点 $u$ 的 $f_{u,0/1}$,然后再做一遍环上 DP。如果这个环没有首尾之间的独立集限制,这其实就是一条链,按照树的方式转移即可。但是首尾之间有限制,我们就先钦定首必不能选,然后做一遍 DP,把尾的 $f_{0/1}$ 算到答案的贡献里,然后钦定首必选(亦可钦定其可选可不选,如果需要求独立集方案,为了不冲不漏,此处要钦定必选),再做一遍 DP,把尾的 $f_0$ 贡献进去,这里就不贡献 $f_1$ 了,不然会不满足首尾之间的限制条件。
**另外一种基环树 DP 形式:**
有人说,我学的基环树 DP 不太一样,是:把环上一条边拎出来,剩下一棵树,然后类似上面的钦定,做两遍树形 DP。这两种方法其实是本质相同的,只不过这种方法把断边后的环当做树上一条链,整体做一遍 DP,相当于把环上 DP 放在树形 DP 里做了。对于仙人掌来说,我们还是喜欢单独对环做 DP。
那么仙人掌上也很好做了。$f$ 的定义便是关于 $u$ 的子仙人掌上的信息。圆点上我们赋初值 $f_{u,0}\gets 0, f_{u,1}\gets 1$。在方点上,我们做环上 DP,然后把答案统计到方点的父亲圆点 $u$ 上。先使得 $u$ 在环尾,然后类似基环树上的环做两遍 DP,得到 $f_{u,0/1}$。在两遍环上的 DP 的时候,不要把答案直接赋给 $f_u$,而是应该使用临时变量存放,做完两遍 DP 后再存到 $f_u$ 里面,这样是为了避免第一次 DP 对第二次 DP 造成的影响。
于是,我们做到了时空线性 $\mathcal{O}(n+m)$ 解决了本题。
-----
做完这题可以去尝试一下 [\[SDOI2010\] 城市规划](https://www.luogu.com.cn/problem/P2478),树套环上求至少间隔两个位置的最大独立集,可以参考[我的题解](/XuYueming/p/18300089)。
**Solution:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
从最简单的树开始思考,然后想想基环树怎么处理,最后思考仙人掌上的问题,是我们处理此类问题的一般模式。这是由 $0$ 个环,到 $1$ 个环,再到若干个环,不断加强问题的过程。
**例二、静态仙人掌直径([SHOI2008] 仙人掌图,link、link、link):**
**Problem Statement:**
给你一个有 $n$ 个点和 $m$ 条边的仙人掌,求它的直径。直径被定义为两点间最短距离的最大值。
$n\leq 5\times 10^4$,$m\leq 10^7$。
**Problem Analysis:**
树的直径是经典的(猜你想找:[Longest path in a tree](https://www.luogu.com.cn/problem/SP1437))。我们有两种解法,一种是两遍 DFS,但是它碰到负权边就挂了,而且不太具有可拓展性;另一种解法是树形 DP,记 $f_u$ 表示从 $u$ 开始往叶子的方向走,最长距离是多少,枚举 $v\in \operatorname{son}(u)$,先贡献答案 $D\Leftarrow f_u+f_v+1$,再做 DP $f_u\Leftarrow f_v+1$。(其中 $a\Leftarrow b$ 表示 $a\gets\max\{a,b\}$。)
基环树求直径是经典的(猜你想找:[\[IOI 2008\] Island](https://www.luogu.com.cn/problem/P4381),[\[NOI2013\] 快餐店](https://www.luogu.com.cn/problem/P1399),但是需要说明的是,这两题形式和本题相同,但是对直径的定义都略有不同,以下按照本题的定义分析)。先跑树形 DP,该贡献答案的贡献到答案里去,然后得到环上每一个点的 $f$,考虑一条经过环边的路径,设 $\{c_m\}$ 表示这个环,那么这条路径形如:$u \stackrel{\displaystyle f_{c_i}}{\longrightarrow} c_i \stackrel{w(i,j)}{\longrightarrow} c_j \stackrel{\displaystyle f_{c_j}}{\longrightarrow} v$,其中 $w(i,j)$ 表示环上第 $i$ 个点到第 $j$ 个点之间的最短距离,即为 $\min\Big\{j-i,m-(j-i)\Big\}$。考虑怎么求出 $f_{c_i}+w(i,j)+f_{c_j}$ 的最大值。我们先拆换成链,再复制一份接在后面。枚举 $i$ 和小于它的 $j$,强制让 $w(j,i)$ 就等于 $i-j$,此时 $j$ 需要满足的条件为 $i-j\leq m-(i-j)$ 即 $j\geq i-\lfloor m/2\rfloor$,如此,我们统计的信息就是 $\max\limits_{j=i-\lfloor m/2\rfloor}^{i-1}\Big\{f_{c_j}-j\Big\}+i+f_{c_i}$,滑动窗口最值,可以用单调队列维护。注意到,这样我们并不会漏掉某一种情况。
那么仙人掌求直径也是简单的。我们在方点统计完答案的贡献后,还要处理出方点的父亲圆点 $u$ 的 $f$ 值,这个直接枚举环上另一个点 $v$ 就可以了。
时空复杂度 $\mathcal{O}(n+m)$。
**Solution:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
通过这两道板子题,相信你已经对静态仙人掌上全局问题的求解有了清晰的认识。
以上,我们了解了静态仙人掌上统计全局信息的方法。尽管我们并没有把圆方树建出来,我们还是可以想象在一棵虚拟的圆方树上求解问题:在一个方点上,处理这环上的信息,把孩子圆点的信息合并到父亲圆点中去;在一个圆点上,我们赋 DP 初值。这也是标题中「一种关于点双连通分量的思考方式」的体现,我们解题可能不需要圆方树,但是思考过程会借助圆方树方便思考。
#### 所有路径类问题
如果你需要统计所有路径的信息,树上我们可能需要用到点分治。那么在仙人掌上,我们要对圆方树进行点分治,类似于树上,对于一个点统计经过这个点的信息。理论上来说点分树也可以被应用在仙人掌上。
由于作者还没有学习到 FFT,例题暂时不能完成,这部分暂且不展开。
#### 所有「子仙人掌」类问题
树上这类问题我们有 **树上启发式合并(DSU on tree)** 的做法,也可以使用线段树合并优化。
根据结论,子仙人掌对应圆方树的子树,问题就被放到圆方树上,真的成了一棵树上的问题了。
**例三、persistent DSU on cactus(link):**
**Problem Statement:**
$n$ 个点 $m$ 条边的仙人掌,每个结点有一个颜色 $c_u$。
$q$ 次询问 $(u,k)$,求 $u$ 的子仙人掌中出现次数不小于 $k$ 的颜色的颜色编号和。
$u$ 的子仙人掌被定义为:断开在 $1,u$ 所有简单路径上出现过的边后,$u$ 所在的连通块。
不知道为什么出题的时候出成了强制在线。只要空间复杂度别太离谱就行。
$2\leq n\leq10^5$。$1\leq q\leq 10^5$。$k\leq n$。$c_u\in[1,n]$。
**Problem Analysis:**
离线 DSU on tree,时间复杂度两只 $\log$,如果强制在线,其实就是需要树状数组的在每一个结点上的版本。换成一个可以支持:继承、单点修改、区间查询的数据结构,就是主席树。
**Solution:**
**Code:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
**Gen:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
#### 分别以每个点为根求解
树上这类问题我们有 **换根 DP** 的做法,仙人掌上也可以类似做换根 DP。
**例四、GAME on cactus(link):**
**Problem Statement:**
小 X 和小 Y 来到一棵 $n$ 个点 $m$ 条边的仙人掌上玩游戏,点编号为 $1\sim n$。
一开始某个节点上有个棋子,小 X 和小 Y 轮流移动这个棋子,已经走过的边不能再走,谁不能移动谁就输了。
小 Y 先手,她向你求助,对于每一个节点,若其作为初始放置棋子的节点,她是否有必胜策略?
$2\leq n\leq2\times10^5$。
**Problem Analysis:**
见[我的题解](https://www.cnblogs.com/XuYueming/p/18992600)。
**Solution:**
**Code:**
见[我的题解](https://www.cnblogs.com/XuYueming/p/18992600)。
**Gen:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
### 类型二:静态仙人掌,维护点对间所有简单路径信息
这类问题需要我们支持:修改点权或边权,询问点对之间路径上信息。
**例五、仙人掌点对间最短路长度(【模板】静态仙人掌,link):**
**Problem Statement:**
给你一个有 $n$ 个点和 $m$ 条边的仙人掌,和 $q$ 组询问,每次询问两点 $u,v$ 间最短路长度。
$n\leq 10^4$,$m\leq 2\times 10^4$,$q\leq 10^4$。
**Problem Analysis:**
属于「边权相关信息」,$\odot=+$,$\oplus=\min$,$+$ 对 $\min$ 有分配律,可以求解。
对于原子信息的求解,我们需要对每个点双维护总环长,对于每个圆点维护,他在他父亲方点代表的环中,到环首的距离。
对于前文提到过的不是环的点双,特殊处理成一个环即可。
于是,我们可以在 $\mathcal{O}\Big(m+(n+q)\log n\Big)$ 或者长链剖分优化求 kth-father $\mathcal{O}(n\log n + q+m)$ 的时间复杂度内求解问题。
**Solution:**
均采用倍增维护树上信息。
**正常圆方树,采用树上前缀和预处理信息:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
**正常圆方树,采用弹边栈预处理信息:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
**不设置方点的圆树:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
**正常圆方树,使用 <code>vector</code> 处理信息:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
接下来看有修改的问题。
对于前文分析的特殊点权相关信息,由于其对于仙人掌的形态没有要求,所以将在[无向图部分例题十四](#exampleP14)给出一种实现方式。
**例六、BUY on cactus(link):**
**Problem Statement:**
小 Y 来到一棵 $n$ 个点 $m$ 条边的仙人掌上旅游,并希望通过买卖赚差价,点编号为 $1\sim n$。
在一次旅游时,她告诉你旅游的起点和终点 $u,v$。她会选择一条以 $u,v$ 为端点的**简单路径**,并在路上选择一个结点 $u'$,花费 $c_{u'}$ 的代价购入某个物品,再选择一个结点 $v'$,以 $w_{v'}$ 的价格卖出,获得 $w_{v'}-c_{u'}$ 的利润。显然她必须先购入才能卖出,但 $u'$ 可以等于 $v'$。她不能啥也不做。小 Y 问你,在最优计划下,她能够获得的利润最大值,这个值可能为负。
由于这棵仙人掌很不稳定,每一个点的 $c_u,w_u$ 都可能发生变化。你需要支持这种修改的同时,能够回答小 Y 的问题。具体来说,总共有 $q$ 次修改或询问。
$2\leq n\leq2\times10^5$,$1\leq q\leq 10^5$。
**Problem Analysis:**
购买类问题是十分经典的,我们就做过静态树上的问题:[POJ-3728 The merchant](http://poj.org/problem?id=3728)。
需要维护的信息是什么?千万不要矩阵学傻了,说需要维护矩阵。我们可以维护三元组 $(\mathrm{mic},\mathrm{mxw},\mathrm{ans})$,分别表示 minimum cost, maximum value and answer(最小花费、最大收益和路上的答案)。树上我们只需要考虑拼接两条简单路径的情况,有:
$$
\begin{matrix}
(\mathrm{mic}_1,\mathrm{mxw}_1,\mathrm{ans}_1)+(\mathrm{mic}_2,\mathrm{mxw}_2,\mathrm{ans}_2)\\
\Downarrow\\
\Big(\min\{\mathrm{mic}_1,\mathrm{mic}_2\},\max\{\mathrm{mxw}_1,\mathrm{mxw}_2\},\max\{\mathrm{ans}_1,\mathrm{ans}_2,\mathrm{mxw}_2-\mathrm{mic}_1\}\Big)
\end{matrix}
$$
一步一步来看看这个模型怎么放到仙人掌上。
首先对于每一个环,可以拉下来变成一个序列,容易得到每一个点,通过左链和右链到环顶的两个信息,注意潜在的信息合并顺序问题。我们需要将这两个信息或起来,而不是上文的 $+$ 运算:
$$
\begin{matrix}
(\mathrm{mic}_1,\mathrm{mxw}_1,\mathrm{ans}_1)\cup(\mathrm{mic}_2,\mathrm{mxw}_2,\mathrm{ans}_2)\\
\Downarrow\\
\Big(\min\{\mathrm{mic}_1,\mathrm{mic}_2\},\max\{\mathrm{mxw}_1,\mathrm{mxw}_2\},\max\{\mathrm{ans}_1,\mathrm{ans}_2\}\Big)
\end{matrix}
$$
我们于是可以得到它与方点父亲之间的边权,注意潜在的方向问题。
其实已经解决了整个问题。修改的时候修改重儿子,查询的时候跳重链,链顶轻儿子特殊查询。可以参考示例代码。
时间复杂度:$\mathcal{O}(m+n\log n+q\log^2n)$。单次修改 $\mathcal{O}(\log n)$,单次查询 $\mathcal{O}(\log^2n)$。
**Solution:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
**Gen:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
### 类型三:静态仙人掌,支持维护链和子仙人掌
回想我们树上树链剖分可以支持什么操作?树链、子树修改,树链、子树查询。那么由于仙人掌具有一定树的形态,我们也可以将仙人掌剖分,实现长链(短链)修改、子仙人掌查询。接下来考虑的信息均是点权。
回顾我们是如何定义仙人掌上的链的,以及不要忘记,在仙人掌中每经过一个奇环时,若始终选择在环上走最长(或最短)的路径,则整条走出的路径即为 $u, v$ 间的长链(或短链)。
我们不妨先只考虑如何修改 $u,v$ 间的长链。拆解问题,如果 $p=\operatorname{lca}(u,v)$ 是个圆点,相当于修改 $u\rightarrow p$ 和 $p\rightarrow v$ 两条长链;否则 $p$ 为方点,除了 $u\rightarrow u'$ 和 $v'\rightarrow v$ 这两个和 $p$ 为圆点时形式相同的子问题,还有一个环上 $u'\rightarrow v'$ 最长路的问题。
先考虑如何修改一对具有祖先关系的 $u,v$ 之间的长链。树链剖分后,在圆方树上跳一段重链时,DFS 序上对应的连续一段区间为圆方树上这条重链。树上我们需要的正是一段连续的区间,因为这样我们就可以用数据结构来维护了,但在仙人掌上,这是不对的,我们要修改的不是这样一条圆方交错的圆方树树链,而是需要修改仙人掌上长链的每一个点。
我们不妨修改一下这个 DFS 序,使得对于这样连续一段区间,完整包含了我们需要修改的点。并且显然我们不需要方点出现在 DFS 序上,因为它身上没有我们需要维护的信息。
对于方点,我们先把其轻儿子放到 DFS 序后面,再放其重儿子,接着处理重儿子的子仙人掌,最后处理其他轻儿子的子仙人掌。从 DFS 序的角度上考虑,相当于把一个方点替换成了它的所有轻孩子,那么这个方点对应的环就完整地出现在了我们的区间上。
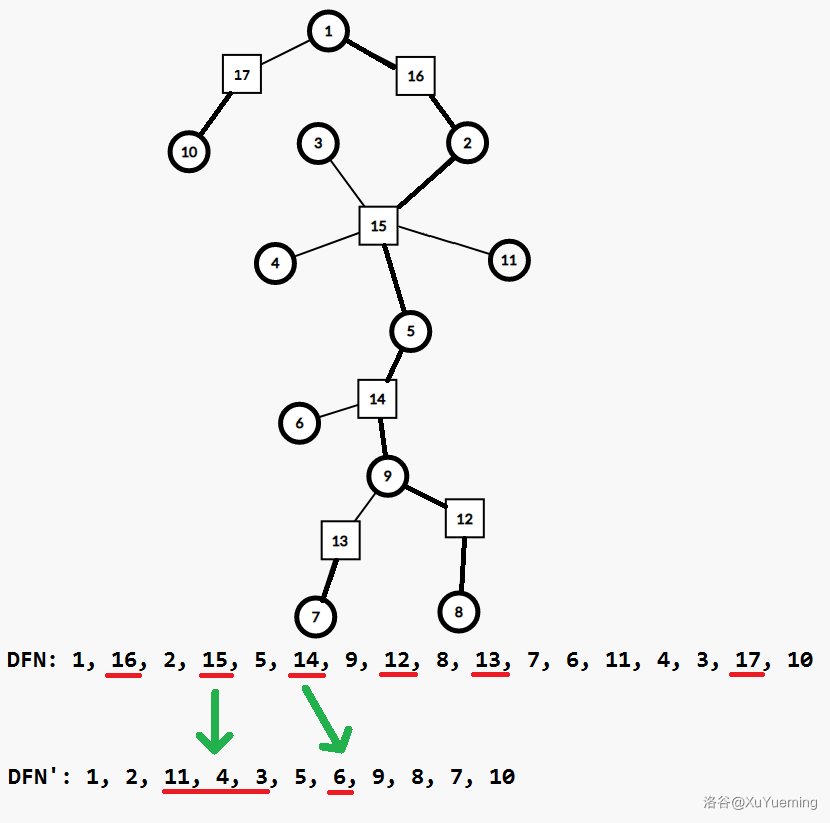
举个例子,比如 $1\sim 9$ 这条重链,原先 DFS 序上对应区间为 $[1,7]=\{1,16,2,15,5,14,9\}$。而在修改后,方点 $15$ 变为了其所有轻儿子 $\{11,4,3\}$,$14$ 同理变成了 $6$,修改后的 DFS 序对应区间为 $[1,8]=\{1,2,11,4,3,5,6,9\}$,涵盖了 $1\sim 9$ 长链上的所有点 $\{1,2,3,4,5,6,9\}$。
完整包含了还不够,我们还需要能够精准的修改想要修改的点。例如,例子中 $11$ 点出现在了区间上,而它不在 $1\sim 9$ 的长链上,这等价于它不在 $2\sim 5$ 环上最长路径上。由于重儿子的唯一性,这启示我们将一个方点的所有轻儿子分类,分为「在重儿子到父亲圆点(原图上)的最长路上」和「在重儿子到父亲圆点(原图上)的最短路上」两种类型,这是方便处理出来的。例如,$11$ 属于后者,而 $3,4$ 属于前者。现在我们区间上有三种类型的圆点,因为不要忘了重儿子也是一种圆点。每次我们只需要将对应类型的轻孩子,和所有重儿子修改就行了。这个是可以用线段树维护的。
至此,我们通过修改 DFS 序,和使用线段树的区间分类修改操作,完成了「修改一段重链对应原仙人掌上的长 / 短链」。
仔细思考一下,在将其推广到一对具有祖孙关系的节点的链修改时,还有细节没有处理。重链拆分后,对于 $v\rightarrow u$ 这条重链($v$ 是链顶),当 $u$ 为圆点且 $v$ 为方点时,根据上面讨论,对应区间为 $v$ 第一个轻儿子在 DFS 序的位置,到 $u$ 在 DFS 序中的位置。当 $v$ 也为圆点时,我们不能将区间左端点设为 $v$ 在 DFS 序中的位置,如下图:
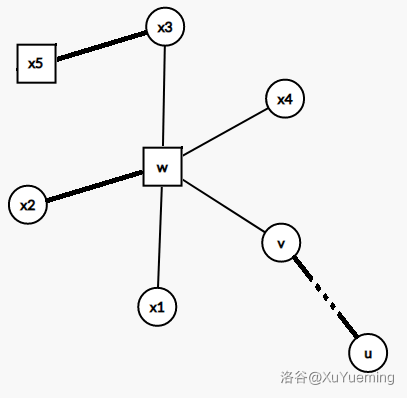
它的 DFS 序如下:
$$
x_3,\colorbox{#409eff}{$ (x_5) $},\colorbox{#409eff}{$ x_4,v,x_1,x_2,\colorbox{#e6a23c}{$ (x_2) $},\colorbox{#e6a23c}{$ (x_4) $},\colorbox{#e6a23c}{$ ...,u $},\colorbox{#e6a23c}{$ (x_1) $} $}
$$
如果我们取出的区间为:
$$
v,x_1,x_2,\colorbox{#e6a23c}{$ (x_2) $},\colorbox{#e6a23c}{$ (x_4) $},\colorbox{#e6a23c}{$ ...,u $}
$$
就会出错,因为包含了 $(x_2),(x_4)$ 这两个无关的子仙人掌对应的区间,以及 $x_1,x_2$ 不一定就是我们需要修改的点,如果我们需要修改长链,就需要修改 $x_4$,而它却没有出现在我们取出的区间上。
我们可以特殊处理。对于 $...,u$,这是链顶为方点的情况,正常处理即可。剩下就是在 $w$ 对应的环上,修改 $v\sim x_3$ 的长链 / 短链,这和 LCA 处的问题形式相同。接下来,我们就可以在 $x_3$ 继续往上跳重链。
如果 $u$ 为方点呢?注意到,我们上述过程实际保证了 $u$ 时刻为圆点,就不需要考虑 $u$ 为方点的情况了。
我们已经可以「修改一对具有祖孙关系 $v,u$ 间的长 / 短链」。在修改过的 DFS 序上,考虑能不能支持 LCA 处的操作,即修改环上一段连续的链。
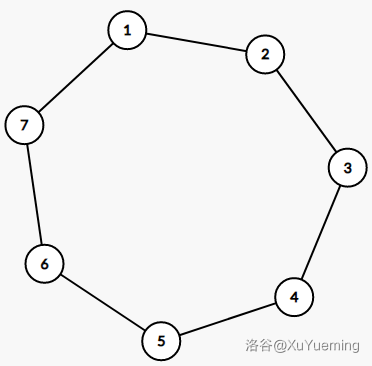
以上图为例,我们假设这个点双对应的方点为 $u$,$u$ 的父亲圆点为 $1$,重儿子为 $5$。按照我们上面的定义,$2,3,4$ 在 $5$ 到 $1$ 的最长路上,是一类轻儿子,$6,7$ 则是另一类轻儿子。这个环对应 DFS 序可以为 $1,{\color{red}7},{\color{yellow}2},{\color{yellow}4},{\color{red}6},{\color{yellow}3},5$,也可以为 $1,{\color{red}7},{\color{red}6},{\color{yellow}2},{\color{yellow}3},{\color{yellow}4},5$ 或者 $1,{\color{yellow}4},{\color{yellow}3},{\color{yellow}2},{\color{red}6},{\color{red}7},5$,上述三种 DFS 序都是符合目前我们要求的,但是为了解决 LCA 处的问题,我们需要环上连续一段链在 DFS 序上被拆分为 $\mathcal{O}(1)$ 个区间,也就希望 DFS 序为后两者,或类似后两者的形态。很容易在类似后两种 DFS 序的形态中,拆出我们想要的区间。例如考虑 DFS 为 $1,{\color{red}7},{\color{red}6},{\color{yellow}2},{\color{yellow}3},{\color{yellow}4},5$,那么 $3\rightarrow7$ 的长链为 $3,4,5,6,7$,对应 DFS 序区间是 $[5,6]\cup[7,7]\cup[2,3]$。
剩下只有子仙人掌操作没有解决了,但是我们惊讶地发现,在修改后的 DFS 序上,在一定程度上很好地保留了 DFS 序一段区间对应子树这个性质,而子仙人掌就是圆方树的子树。具体来说,我们发现 $u$ 的子仙人掌被拆分成了两部分,一部分是 $u$ 本身这个点,另一部分为它的不包括本身的子仙人掌。那么只需要分别查询这两段区间的信息就行了。
对于代码实现上的细节,请参考例题代码。时间复杂度瓶颈在于线段树。
**例七、【清华集训2015】静态仙人掌(link):**
**Problem Statement:**
一棵 $n$ 个点、$m$ 条边的仙人掌,指定 $1$ 为根。每个结点有一个颜色(黑或白),初始时均为黑色。有 $q$ 次操作:
1. 将 $u$ 到根的最短路径 / 最长路径上所有点的颜色取反。
1. 询问点 $u$ 子仙人掌中的黑点数目。
$n,q\leq 5\times10^4$。
**Problem Analysis:**
问题严格弱于前文的分析的模型,可以用线段树方便维护。可以参考示例代码的具体实现。
时间复杂度:$\mathcal{O}((n+q)\log n)$。
**Solution:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
### 类型四:静态仙人掌,求给定点集的整体信息
这类问题每次询问会给出一个点集,求这个点集的整体信息,比如统计一些东西,做一些 DP 什么的,类似于类型一,只不过只关于点集中的点了。
对于树上给定点集的问题,我们可以建出这些点的虚树,在虚树上统计答案,做树形 DP。由于点集 $S$ 对应虚树结点个数是 $\mathcal{O}(|S|)$ 的,时间复杂度得到了保证。
唯一需要注意的是,对于方点 $u$,其虚树上一个孩子 $v$,那么不能想当然地认为 $v$ 是 $u$ 的孩子圆点,事实上,$v$ 并不一定是其孩子圆点,甚至连个圆点都可能不是。所以,我们需要通过一些方法求出 $v'$,这个才是 $u$ 的孩子圆点。
**例八、mx 的仙人掌(link):**
**Problem Statement:**
一棵 $n$ 个点、$m$ 条边的仙人掌。
$q$ 此询问,每次给出一个点集 $S$。求出从 $S$ 中选出两个点 $u,v$,他们之间最短路的最大值是多少,$u,v$ 可以相同。
$n,\sum|S|\leq3\times10^5$。
**Problem Analysis:**
每次可以 $\mathcal{O}(n)$ 类似类型一求直径,做一遍圆方树上的树形 DP。
那么先把虚树建出来。然后考虑在 LCA 处统计答案,即枚举 LCA $p$,考虑它两个孩子的子树中的点 $u,v$ 对答案的贡献。分 $p$ 为方点、圆点讨论。
1. $p$ 为圆点:
此时 $u,v$ 之间的最短路即为 $s_u+s_v-2s_p$,其中 $s_u$ 表示圆方树边权的树上前缀和。我们只需要求出 $s_u+s_v$ 的最大值。这个很容易,对于每个点 $u$ 维护 $f_u$ 表示子树中 $s_u$ 的最大值,然后就可以统计了。
1. $p$ 为方点:
设 $u',v'$ 表示 $p$ 在圆方树上两个孩子,对应为 $u,v$ 的祖先。$u',v'$ 可以 kth-kather 求出。此时 $u,v$ 之间的最短路为 $s_u-s_{u'}+s_v-s_{v'} + \min\{|d_{v'}-d_{u'}|,\operatorname{sum}(p)-|d_{v'}-d_{u'}|\}$,其中 $\operatorname{sum}(p)$ 表示方点 $p$ 对应的环的总长,$d_u$ 表示 $u$ 到环首的距离。相当于 $p$ 的每个孩子 $u$ 有一个点权 $w_u=f_u-s_u$,要求 $\max\limits_{u,v\in\operatorname{son}(p)}\Bigg\{w_u+w_v + \min\Big\{|d_v-d_u|,\operatorname{sum}(p)-|d_v-d_u|\Big\}\Bigg\}$,这个可以拆换成链,再复制一份接在后面,然后就能单调队列做了。
时间复杂度为:$\mathcal{O}(m+n\log n+\sum|S|(\log|S|+\log n))$。
**Solution:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
**使用 [$\mathcal{O}(1)$ 查找 $u',v'$ 算法](https://www.cnblogs.com/XuYueming/p/18919143):**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
**例九、【集训队互测2016】火车司机出秦川(link):**
**Problem Statement:**
一棵 $n$ 个点、$m$ 条边的仙人掌,有边权,和 $2q$ 次操作。
询问,第 $i$ 次询问有 $k_i$ 条简单路径,称作「路径」。一条「路径」用三个整数 $(u,v,0/1)$ 表示,其中 $u,v$ 表示它的端点,$0$ 表示「路径」为 $u,v$ 之间所有简单路径中经过最少结点的那条,$1$ 表示经过最多结点的那条。保证「路径」端点不重复,保证所有环为奇环。求这些「路径」的并的边权和。
每次询问后可能跟着一条边权的修改。
$n,\sum|k_i|\leq3\times10^5$。
**Problem Analysis:**
先把这些「路径」的端点在圆方树上的虚树建出来。下称经过最少城市的路径称作最短路,与边权最短路区别,同理最长路。
考虑哪些东西会对答案产生贡献,也就是考虑一条「路径」可能会包含哪些边。LCA $p$ 若是圆点,就包含了 $p\rightarrow u$ 和 $p\rightarrow v$ 的最长 / 最短路。$p$ 若是方点,就包含了 $u'\rightarrow u$,$v'\rightarrow v$ 的最长 / 最短路,这个和前面的问题形式是相同的,以及 $p$ 对应环上 $u'\rightarrow v'$ 的最长 / 最短路。
先不考虑修改,如果只有第一种问题怎么求。一条虚树边对应圆方树上一条方圆交错的路径,在原仙人掌上体现为,若干个简单环被连接成一个链状的结构。差分之后做树上前缀和,就能知道一条虚树边是否需要统计最短 / 最长路。而知道了是否需要统计最短 / 最长路,我们也很方便求出这一条链的贡献了。记 $s_{0/1}(u)$ 表示 $u$ 到根的最短 / 最长路路径长度,好像这样可以计算了,对于只需要统计最短 / 最长路,就是 $s_{0/1}$ 相减,对于两个都需要统计,就是 $s_0(u)+s_1(u)$ 相减……吗?对于环来说,最短最长路加在一起正好凑成了一个整个环,但是对于一条非环边来说就被重复统计了。所以此时对于「两点被一边相连」这种点双不能再当做一个环考虑了。还需要维护 $s_2(u)$ 表示 $u$ 到根的非环边路径长度。两种路径都要统计时,就是 $s_0(u)+s_1(u)-s_2(u)$ 相减。
考虑如果只有第二种问题怎么求。不妨令在环的顺序下 $u'$ 在 $v'$ 之前,那么最短 / 最长路,就是 $u'\sim v', v'\sim tail\sim head\sim u'$ 这两条路径中较短 / 长的那条。可以用差分完成区间覆盖,然后也能统计了。
如果两种问题同时存在,需要注意,第一种问题的路径可能会经过第二种路径的环,这个在第二个问题里面特殊处理一下,看看需不需要额外添加一些覆盖区间。
如果有了修改呢?如果这是一条环边,会影响到:总环长,这个很好维护;增加环上后缀所有点的到环首距离,所以需要对每个环开一个树状数组;对连续一段子树的 $s_{0/1}$ 造成影响,这个用树状数组维护 DFS 序,就是区间加。如果这是一条非环边,会对子树的 $s_{0/1/2}$ 产生增量,这个也用树状数组维护。
时间复杂度:$\mathcal{O}(m+(n+q+\sum|S|)\log n)$。
**Solution:**
给出了没有修改的部分分代码,方便理解。
**没有修改:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
**满分做法:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
### 类型五:静态仙人掌,动态维护全局信息
其实就是仙人掌上的 DDP 问题。
我们不妨从一个具体的问题开始思考:支持修改点权,动态维护仙人掌的最大独立集权值。
在树上,我们做过[模板题](https://www.luogu.com.cn/problem/P4719),没有修改时,我们在前文[例题一](#exampleP1)探讨过单次 $\mathcal{O}(n)$ 求仙人掌最大独立集的算法,我们要做的就是把这两个算法结合起来。
回顾在一个序列上我们如何动态维护独立集的?设 $f_0,f_1$ 表示选或不选最后一个元素的最大独立集,那么根据定义有 $f_1'=f_0+a_i,f_0'=\max\{f_0,f_1\}$,容易写出转移方程的 $(+,\max)$ 矩阵乘法形式:
$$
\begin{bmatrix}
f_0 & f_1
\end{bmatrix}
\times
\begin{bmatrix}
0 & a_i \\
0 & -\infty \\
\end{bmatrix}
=
\begin{bmatrix}
f_0' & f_1'
\end{bmatrix}
$$
回顾这个东西是如何上树的。我们轻重链剖分后,重链其实就是普通的一条链,但是对于不选择 / 选择 $u$ 的收益不再是 $0/a_u$,而是 $t_0/t_1+a_u$,其中 $t_{0/1}$ 表示轻儿子对它的贡献,$t_0$ 为所有轻儿子的 $\max\{f_0,f_1\}$ 之和,$t_1$ 为所有轻儿子的 $f_0$ 之和。转移矩阵为:$\begin{bmatrix}
t_0 & t_1+a_u \\
t_0 & -\infty \\
\end{bmatrix}$。如此,我们实际完成了,通过求一条以 $u$ 为链顶的重链的矩阵乘法,得到 $u$ 子树的答案。
这个东西怎么上仙人掌呢?无非就是考虑如何处理环。

目前状态肯定是不够了,想到把扩展状态成 $f_0,f_1,g_0,g_1$,分别对应环尾必不选和可能选的 DP 值。但是这是不好做的。如上图,假设这个点双对应的方点为 $u$,$u$ 的父亲圆点为 $1$,重儿子为 $5$。为了转移顺序,我们也许会想到把 DFS 序设置为:
$$
7,6,\colorbox{#409eff}{$ 5,... $},4,3,2
$$
但是 $5,...$ 得到的是 $5$ 的子仙人掌的 DP 值,我们并不能将它再乘上某一个矩阵,得到对应在 $f_0,f_1,g_0,g_1$ 上的转移矩阵。所以这个想法是错误的。
以上想法错误之处,根本在于重儿子不能出现在转移方程的中间,否则无法通过 DP 值得到对应的转移矩阵。那么 $5$ 作为 DP 的初始位置,应该如何设置转移顺序和状态呢?
我们想到一种「兵分两路」的转移方式,将环拆成两条链:$5,6,7,1$ 和 $5,4,3,2$,并要求 $5$ 要么同时选,要么同时不选,最后统计答案的时候 $1,2$ 不能同时选。设 $f_{a,b}$,其中 $a,b$ 分别表示左右两条链,目前考虑到的链顶选或不选的答案。初始矩阵为:
$$
\begin{bmatrix}
f_{0,0}&f_{0,1}&f_{1,0}&f_{1,1}
\end{bmatrix}
=
\begin{bmatrix}
t_0&-\infty&-\infty&t_1
\end{bmatrix}
$$
其中 $t_{0/1}$ 表示重儿子 $5$ 传统的 DP 值。这同时解决了 $5$ 只能最多选一次的问题。
对于左边这条链上的点 $u$,会独立转移 $f_{0/1,*}$,即对于 $p=0,1$,$f_{0,p}'=\max\{f_{0,p},f_{1,p}\}+t_0,f_{1,p}'=f_{0,p}+t_1$,其中 $t_{0/1}$ 表示 $u$ 考虑其子仙人掌的传统 DP 值,下文在不引起歧义的前提下,省去了对 $t_{0/1}$ 的解释。写成转移矩阵的形式就是:
$$
f(t_0,t_1,1)=\begin{bmatrix}
t_0 & & t_1 & \\
& t_0 & & t_1 \\
t_0 & & & \\
& t_0 & & \\
\end{bmatrix}
$$
同理,对于右边那条链上的 $u$ 的转移为:
$$
f(t_0,t_1,2)=\begin{bmatrix}
t_0 & t_1 & & \\
t_0 & & & \\
& & t_0 & t_1 \\
& & t_0 & \\
\end{bmatrix}
$$
在 $1$ 点,我们就能求出想要的值,不妨令 $1$ 在左侧链上,那么 $t_0=\max\{f_{0,0},f_{0,1}\},t_1=f_{1,0}$,我们可以写出一个矩阵,通过 $\begin{bmatrix}
f_{0,0}&f_{0,1}&f_{1,0}&f_{1,1}
\end{bmatrix}$ 得到 $\begin{bmatrix}
t_0&-\infty&-\infty&t_1
\end{bmatrix}$,这是正是环上 DP 的初始值,从而形成逻辑上的闭环。
$$
M=\begin{bmatrix}
0 & & & \\
0 & & & \\
& & & 0 \\
& & &
\end{bmatrix}
$$
当然,以上所有矩阵都是转移矩阵,我们初始矩阵为:
$$
M_0=\begin{bmatrix}
0 & & & 0
\end{bmatrix}
$$
我们已经初步确认,这个问题是可做的,并且粗浅地想出了一种转移的方式。接下来,需要解决遗留下来尚未处理的细节。
1. 如何设计 DFS 序?
类似类型三的 DFS 序设计,将方点替换为其所有轻孩子,接着是重儿子和它的子树。同时,我们需要左链右链上的节点的相对顺序满足转移顺序。

例如,用不同颜色区分左右链,上图的一个**不合法**的 DFS 序为 ${\color{red}1},{\color{red}7},{\color{yellow}2},{\color{yellow}4},{\color{red}6},{\color{yellow}3},5$,因为右链转移顺序并不是 $3,4,2$,而应该是 $4,3,2$。一种合法的 DFS 序为 ${\color{red}1},{\color{red}7},{\color{yellow}2},{\color{yellow}3},{\color{red}6},{\color{yellow}4},5$。当然,我们显然喜欢更简单的 DFS 序 ${\color{red}1},{\color{red}7},{\color{red}6},{\color{yellow}2},{\color{yellow}3},{\color{yellow}4},5$,它先按照顺序转移完了右链上的 $4,3,2$,再转移完左链上 $6,7,1$。
1. 如何分配 DFS 序上对应转移矩阵?
先来明确一下各种 DFS 序区间和其对应矩阵的关系。
对于一个方点,它对应 DFS 序上的区间求出来的矩阵,是一个环上 DP 未完成的矩阵,因为缺少了链顶的转移。例如,${\color{red}1},{\color{red}7},{\color{red}6},{\color{yellow}2},{\color{yellow}3},{\color{yellow}4},5$ 中,实际方点对应的 DFS 序为 ${\color{red}7},{\color{red}6},{\color{yellow}2},{\color{yellow}3},{\color{yellow}4},5$,这缺少了 ${\color{red}1}$ 的转移。
对于一个重儿子圆点,它对应 DFS 序上的区间求出来的矩阵,已经完成了环上的转移,左乘 $M_0$ 后形如 $\begin{bmatrix}t_0&-\infty&-\infty&t_1\end{bmatrix}$。
对于一个轻儿子圆点,它没有对应的 DFS 序区间。
类似树上,维护 $u$ 所有轻儿子的答案和,记为 $g_0,g_1$,以及不妨令 $g_1$ 中包含 $u$ 的点权。
1. $u$ 为重儿子。
它在 DFS 序上位置形如:$...,u,(a),(b_1),(b_2),...$,其中 $(a)$ 为 $u$ 的重方儿子对应子树,$(b_i)$ 对应 $u$ 的轻方儿子的子树,两个 $...$ 分别对应 $u$ 的轻儿子兄弟,和这些点的方儿子子树。
$(a)$ 求出来一个环上 DP 未完成的矩阵,所以要先乘上 $f(g_0,g_1,1)$ 完成环上 DP,再乘上 $M$,得到形如 $\begin{bmatrix}t_0&-\infty&-\infty&t_1\end{bmatrix}$ 的矩阵。这也就是 $u,(a)$ 求出的结果。
1. $u$ 为轻儿子。
先将 $g_0,g_1$ 加上其重儿子的贡献,然后它在 DFS 序上的矩阵即为 $f(g_0,g_1,\operatorname{type}(u))$。
1. 如何求答案?
$1$ 为链顶的这条重链,对应的区间的矩阵之积,就是转移矩阵,**左乘**初始矩阵 $M_0$ 得到答案矩阵 $\begin{bmatrix}t_0&-\infty&-\infty&t_1\end{bmatrix}$,答案即为 $\max\{t_0,t_1\}$。
1. 如何修改?
树上修改的时候,设当前点为 $u$,其重链顶为 $v$,$v$ 的父亲为 $w$,那么要先在 $w$ 的矩阵中减去这条重链的贡献,再加上修改后的贡献,接着令 $u\gets w$,继续操作,直到 $v=1$ 停止。上述过程中要求我们维护一个 $M_{\mathrm{last}}$ 表示以 $v$ 为链顶的这条重链修改前的矩阵之积。在修改 $w$ 前要先求出 $w$ 所在重链的矩阵之积,以赋值给 $M_{\mathrm{last}}$。
仙人掌上,对于 $v$ 的类型分类讨论。
1. $v$ 为圆点。
我们需要处理 $v$ 的转移矩阵。$v$ 的 $g_0,g_1$ 可以方便维护,那么只需要和初始化的时候一样,求出重儿子的贡献,在线段树上修改即可。发现竟然不需要 $M_{\mathrm{last}}$ 之类的东西。
1. $v$ 为方点。
我们需要处理 $w$ 的转移矩阵。$v$ 作为 $w$ 的轻儿子,就需要在 $w$ 的 $g_0,g_1$ 中,减去原先的贡献,再加上修改后的贡献。于是类似树上 DDP,需要维护 $M_{\mathrm{last}}$,接着,按照 $w$ 为重儿子还是轻儿子,修改其转移矩阵即可。
如何维护 $M_{\mathrm{last}}$?似乎只需要和树上 DDP 类似,当 $w$ 链顶 $p$ 为方点时,先查询 $p$ 对应的转移矩阵,赋值给 $M_{\mathrm(last)}$ 即可。但这在某种情况下是错误的。当 $u=v$ 为圆点时,我们查询 $p$ 的转移矩阵时,会包含 $u$ 的转移矩阵,我们能够保证这个矩阵是没有更新过的吗?不能,因为可能上一次操作为情况 2「$v$ 为方点」,而这会更新到 $u$ 的转移矩阵,所以我们需要在上一次操作,提前判断这种特殊情况,提前赋值 $M_{\mathrm{last}}$,在这一次操作就不对 $M_{\mathrm{last}}$ 赋值。具体可以参考例题代码。
我们至此成功解决了这个问题,时间复杂度 $\mathcal{O}(nw^3\log n+qw^3\log^2n)$,其中 $w=4$ 为矩阵的大小。或许使用全局平衡二叉树可以优化到一只 $\log$,但是没有实现。
我们在上文中探讨了一种经典的 DDP 问题在仙人掌上的求解方式,对于其他 DDP 问题,或许可以参考这种方式解决问题。
**例十、DDP on cactus(link):**
**Problem Statement:**
$n$ 个点 $m$ 条边的仙人掌,点编号为 $1\sim n$,每个结点有一个权值 $w_u$。
$q$ 次点权修改操作,你需要在第一次修改前以及每次修改后,输出这棵仙人掌的最大独立集。
$2\leq n\leq10^5$。$1\leq q\leq 10^5$。任意时刻 $0\leq w_i\leq 10^9$。
**Problem Analysis:**
前文分析的仙人掌上最大独立集问题。给出了一种参考实现。
**Solution:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
**Gen:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
### 类型六:动态仙人掌
删边连边,保证操作前后都是森林,这类动态树问题,我们使用 LCT,SATT 等方式维护原树。
删边连边,保证操作前后都是沙漠,这类动态仙人掌问题,我们使用 LCT,SATT 等方式维护圆方树。
笔者能力有限,以后有时间再来补这一部分。
### 拓展:多层仙人掌
既然仙人掌的形态很像把树上节点替换成环,我们可以尝试把树上每个节点换成一棵仙人掌,如此进行下去,得到多层仙人掌的结构。
熟悉了仙人掌,其实这种结构无非是仙人掌的小拓展罢了,可以使用类似的算法解决。
## 圆方树在「一般无向图」上的应用
相信你已经掌握了如何使用圆方树解决仙人掌的问题,接下来我们将更进一步,学习如何在一般无向图上应用圆方树。
相比仙人掌而言,一般无向图并没有许多良好的性质,问题并不难于仙人掌上对应类型的问题。
### 类型一:单次询问整体信息
**例十一、[APIO2018] 铁人两项(link):**
**Problem Statement:**
给你一张有 $n$ 个点和 $m$ 条边的无向图,你需要统计有序三元组 $(s,c,f)$ 的个数,且需要满足存在一条简单路径依次经过 $s,c,f$。简单路径指不重复经过点的路径。
$n\leq 10^5$,$m\leq 2\times 10^5$。
**Problem Analysis:**
考虑在树上统计三元组的个数。不妨将 $s,f$ 视为地位相等的「端点」,最后答案乘以二即可。设 $g_u$ 表示 $u$ 子树中选出一个端点的方案数,其实就是 $u$ 为根的子树大小。再设 $f_u$ 表示 $u$ 子树中选出一个端点 $v$,再在 $v\sim u$ 这条路径上选出中间点 $c$ 的方案数。$g$ 的转移显然。$f$ 的转移也很简单,分为选不选择 $u$ 为 $c$ 两种情况讨论。对于一个 $v\in \operatorname{son}(u)$,若选择,$f_u\Leftarrow g_v$;若不选择,$f_u\Leftarrow f_v$。其中 $a\Leftarrow b$ 表示 $a\gets a+b$。那么如何统计答案呢?我们考虑不断合并子树的过程,$f_u,g_u$ 的含义为 $u$ 和已经考虑过的子树,构成的一棵以 $u$ 为根子树的信息。注意这个子树和传统意义上以 $u$ 为根的子树之间的区别。考虑这个子树和一个没被合并进来的,以 $v$ 为根的子树,它们之间对答案产生的贡献。显然就是 $f_u\cdot g_v+f_v\cdot g_u$,加号前表示 $c$ 落在以 $u$ 为根的子树中,加号后表示 $c$ 落在以 $v$ 为根的子树中,然后运用加法原理即可,这是不重不漏的。
放到无向图上呢?我们考虑无非就是选取 $c$ 的这一步变得有些复杂——在一个点双中选点而不是在一个点上选点。分为如何转移和如何统计答案两部分思考。记这个点双大小为 $m$。转移很不难想到,设方点的父亲圆点为 $u$,某一个孩子圆点为 $v$,$g_u\Leftarrow g_v$,$f_u\Leftarrow f_v + (m-1)g_v$,这里 $m-1$ 的系数表示,$c$ 可以选择除了 $v$ 以外任意一个点双中的点,对于 $c=v$ 的情况已经统计在 $f_v$ 内了。我们先考虑暴力统计答案,枚举 $m$ 个圆点中两个不同的圆点 $u,v$,然后一样按照 $c$ 放在哪里分类讨论。$c$ 在 $u$ 那一边,$ans\Leftarrow g_u\cdot f_v$;$c$ 在 $v$ 那一边,$ans\Leftarrow g_v\cdot f_u$;$c$ 在点双中除了 $u,v$ 其他的点上,$ans\Leftarrow g_u\cdot g_v \cdot(m-2)$。优化到线性也很简单,用类似前缀和的方法维护 $\sum f_v$ 和 $\sum g_v$ 即可。
时空复杂度 $\mathcal{O}(n+m)$。
注意此题坑点:图可能不连通,对每一个连通块做一遍即可。
**Solution:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
### 类型二:维护点对间所有简单路径信息
先来看一道经典的问题。
**例十二、必经点个数(link,link,link):**
**Problem Statement:**
给你一张有 $n$ 个点和 $m$ 条边的无向图,有 $q$ 次询问,给出点对 $(u,v)$,求从 $u$ 经过一条简单路径到 $v$,必须经过的节点数。
$n,q\leq 5\times10^5$,$m\leq10^6$。
**Problem Analysis:**
放到圆方树上,均被包含的点,就是圆方树上路径上的圆点。这是因为对于非端点的一个圆点,它作为割点是必定会被经过的。于是可以简单求解。
时间复杂度 $\mathcal{O}(m+n+q\log n)$,尽管可以优化到完全线性。
**Solution:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
接下来看一道典型的圆方树维护点对间所有简单路径信息的问题。
**例十三、[ZJOI2022] 简单题(link、link):**
**Problem Statement:**
一张 $n$ 个点、$m$ 条边的无重边无自环连通无向图,带有正整数边权。
一开始图上任意两个简单环的边权和相等。后来其中一部分边的权值改成了新的权值,因此,修改后的图可能没有这个性质。
现在给出修改后的图,同时给出多组询问,每次询问两点 $S, T$ 间所有简单路径权值和对 $998244353$ 取模的结果。
简单环和简单路径指不包含重复节点。
$1 \le n, q \le 5 \times {10}^5$,$n - 1 \le m \le 6.4 \times {10}^5$。
**Problem Analysis:**
一道好题,关键在于分析出图的性质,否则无从下手。
这张图一开始任意两个简单环的边权和相等,这对这张图的形态做了限制,也就是说存在一种赋边权的方式,满足这个条件。
对于每一个点双考虑,因为简单环显然不会横跨两个点双,所以只会对点双内部的结构产生约束。接下来由简单到复杂,确定一个点双可能的形态。
1. 这个点双没有简单环。
也即两个点被一条边连接的情况,显然合法。
2. 这个点双是一个简单环。
显然合法。
3. 这个点双在一个简单环的基础上多了一条简单链。
我们假设多出的一条链的两端是 $S, T$。那么他们之间就被三条简单路径连接。为了方便起见,我们把这三条链看做是连接 $S, T$ 的三条边,边权对应简单链的边权和。
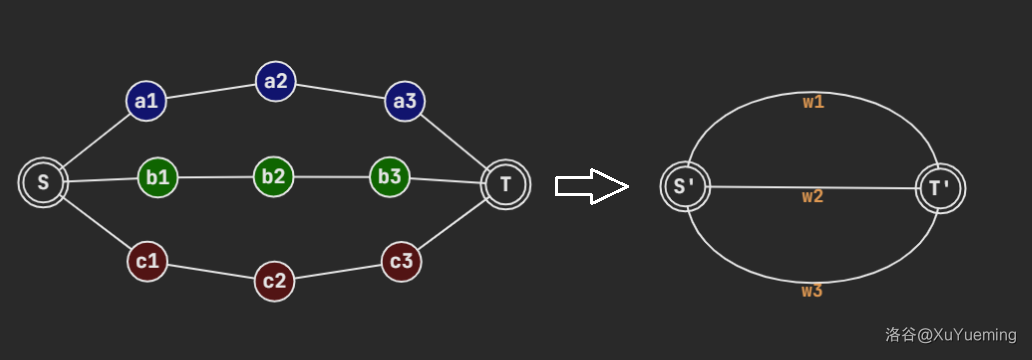
我们只需要说明,存在一种给 $w_1, w_2, w_3$ 赋权的方式,使得任意两个简单环的边权和相等。
图上有三个简单环,设边权和分别为 $s_1, s_2, s_3$,有:
$$
\begin{cases}
s_1=w_1+w_2 \\
s_2=w_1+w_3 \\
s_3=w_2+w_3
\end{cases}
$$
只需令 $w_1=w_2=w_3=k$,其中 $k$ 为任意正整数,就能使 $s_1=s_2=s_3$。
4. 这个点双在一个简单环的基础上,多了若干条以 $S,T$ 为端点的简单链。
类比 case 3 的推导,只需令 $w_1=w_2=\cdots=w_t=k$,其中 $k$ 为任意正整数,就能使 $s_1=s_2=\cdots=s_t$。
5. 这个点双在一个简单环的基础上,多了两条不共端点的平行简单链。
形如:
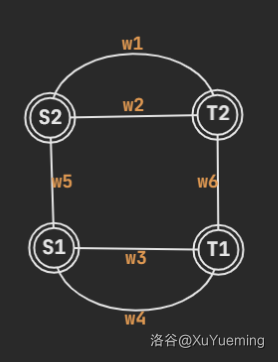
类似地,这里存在六个环:
$$
\begin{cases}
s_1=w_1+w_2 \\
s_2=w_3+w_4 \\
s_3=w_2+w_3+w_5+w_6 \\
s_4=w_2+w_3+w_5+w_6 \\
s_5=w_1+w_3+w_5+w_6 \\
s_6=w_2+w_4+w_5+w_6 \\
\end{cases}
$$
令 $w_1=w_2=w_3=w_4=w_5=w_6$,看看能不能导出什么矛盾。手玩一会后发现,由 $s_1+s_2=s_5+s_6$,得到 $w_5+w_6=0$,而我们的边权都是正整数,所以这是不合法的。
也就是说,一个点双的结构不可能是这样。有趣的是,如果我们令 $w_5=w_6=0$,那么这张图相当于退化成了 case 4 中 $4$ 条链的情况,这似乎在暗示我们 case 4 或许就是我们要找的性质。
6. 这个点双在一个简单环的基础上,多了若干条不共端点的平行简单链。
一定能得到类似 case 5 中的若干条等式,从而导出不可能。
7. 这个点双在一个简单环的基础上,多了两条不共端点的相交简单链。
形如:
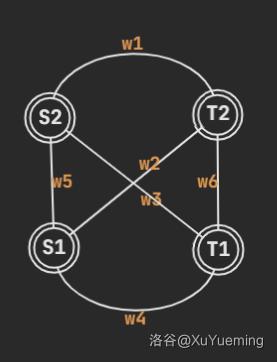
这里同样存在六个环:
$$
\begin{cases}
s_1=w_1+w_2+w_5 \\
s_2=w_1+w_3+w_6 \\
s_3=w_3+w_4+w_5 \\
s_4=w_2+w_4+w_6 \\
s_5=w_1+w_4+w_5+w_6 \\
s_6=w_2+w_3+w_5+w_6 \\
\end{cases}
$$
类似根据 $s_1+s_2=s_5+s_6$ 得到 $w_6=0$,根据对称性同样有 $w_5=0$,这也是不合法的,而且退化后的图也是 case 4 中 $4$ 条链的情况。
8. 这个点双在一个简单环的基础上,多了若干条不共端点的相交简单链。
一定能得到类似 case 7 中的若干条等式,从而导出不可能。
9. 这个点双在一个简单环的基础上,多了若干条不共端点的平行简单链,或相交简单链。
一定能得到类似 case 5 或 case 7 中的若干条等式,从而导出不可能。
从而,我们证明了,只有 case 1、case 2、case 3、case 4 这几种点双的形态是合法的,进一步全部都可以归纳到 case 4 中:存在两个点 $S,T$,他们之间连了若干条简单链。$1,2,3$ 条链分别退化到 case 1、case 2、case 3。
每个点双的形态就是确定的了:
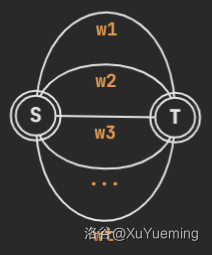
这种图似乎被称作「杏仁」,无论如何,这是一个关键的性质。
肯定需要上圆方树了。
根据经验,不难想到把 $(c,s)$ 这样的二元组作为所求信息,其中 $c$ 表示简单路径条数,$s$ 表示这些简单路径的边权总和。两个信息 $(c_1,s_1),(c_2,s_2)$ 合并后的结果即为 $(c_1c_2,c_1s_2+c_2s_1)$。单位元即为 $(1,0)$。
考虑 $u\rightarrow v$ 的原子信息怎么求。记这个点双中 $S,T$ 间有 $c$ 条简单路径,边权和为 $s$,对于不为 $S,T$ 的点 $u$,定义 $\operatorname{from}(u)$ 表示 $u$ 在 $c$ 条简单路径中的哪一条上,$\operatorname{disS}(u)$ 表示 $S$ 通过 $\operatorname{from}(u)$ 到 $u$ 的距离,$\operatorname{depthS}(u)$ 类似表示 $S$ 通过 $\operatorname{from}(u)$ 到 $u$ 的边的条数,类似定义 $\operatorname{disT}(u),\operatorname{depthT}(u)$。接下来分类讨论。
1. $u=S,v=T$:
信息即为 $(c,s)$。
1. $u=S,v\neq T$:
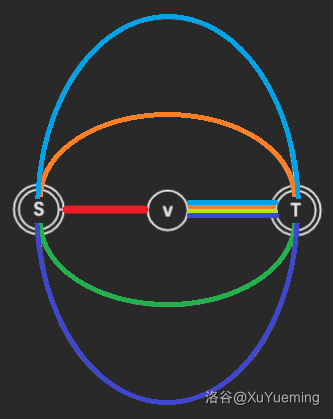
信息为 $\Big(c,s+\operatorname{disT}(v)\cdot(c-1-1)\Big)$,$c-1-1$ 表示 $v\rightarrow T$ 这条边被 $c-1$ 条路径经过,但是已经在 $s$ 中贡献了一次,所以是 $c-1-1$。
1. $u,v\not\in\{S,T\},\operatorname{from}(u)=\operatorname{from}(v),\operatorname{depthS}(u)\leq\operatorname{depthS}(v)$:
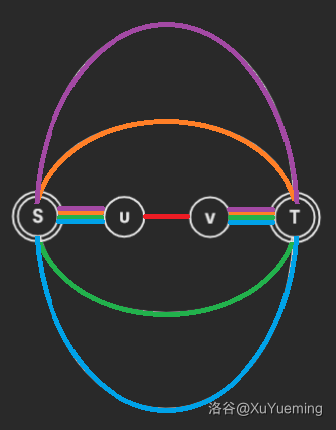
信息为 $\Big(c,s+(\operatorname{disT}(v)+\operatorname{disS}(u))\cdot(c-1-1)\Big)$。
1. $u,v\not\in\{S,T\},\operatorname{from}(u)\neq\operatorname{from}(v)$:
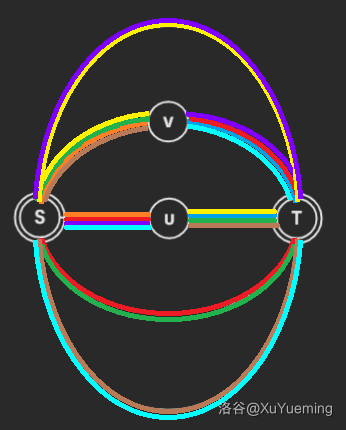
信息为 $\Big(2c-2, 2s + (\operatorname{disS}(u)+\operatorname{disT}(u))\cdot(c-1-2) + (\operatorname{disS}(v)+\operatorname{disT}(v))\cdot(c-1-2)\Big)$。
剩下的情况都是对称的,此略去。
至于如何求出这些信息,只需要把点双的子图建出来,这就是前文仙人掌部分提到的弹边栈的方式,在弹出一条边的时候,在另一张图上加边。这另一张图就是这个点双的子图,根据度数找出 $S,T$ 后,就可以方便处理出其他信息了。
于是我们可以套用圆方树多次询问点对信息的模式方便求解。
这个信息显然满足交换律,所以不需要考虑合并信息的顺序。
在了解圆方树后,这份代码实现起来并不困难。
时间复杂度 $\mathcal{O}(m+n\log n+q\log n)$。
**Solution:**
**圆方树:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
**圆树:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
接下来我们来看一道特殊的带修改的问题。
**例十四、Tourists(link):**
**Problem Statement:**
一张 $n$ 个点、$m$ 条边的连通无向图,带有点权。你需要支持:
1. 修改点权。
1. 询问 $u,v$ 为端点的所有简单路径中,点权最小值的最小值。
$1\leq n,m,q\leq 10^5$。
**Problem Analysis:**
方点在圆方树上的点权为,它的所有孩子圆点在原图上的点权的最小值。圆点的在圆方树上的点权为最小值的单位元,即 $\infty$。
给出树链剖分维护圆方树的实现方式。
**Solution:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
### 类型三:求给定点集的整体信息
来看一道没有显式建出虚树,而是利用虚树结构解决的问题。
**例十五、[SDOI2018] 战略游戏(link):**
**Problem Statement:**
一张 $n$ 个点、$m$ 条边的连通无向图。
$q$ 此询问,每次给出一个点集 $S$。你可以选择一个不在 $S$ 中的点,如果存在 $S$ 中两个点,在不经过你选择的这个点的前提下,不能够到达对方,那么这个方案就是合法的。求你有多少种选点的方案。
$2\leq n\leq10^5$,$n-1\leq m\leq2\times10^5$,$1\leq q\leq10^5$,$\sum|S|\leq2\times10^5$。
**Problem Analysis:**
圆方树上,如果存在一个圆点,删去它之后的若干个连通块中,如果至少有两个连通块中都有 $S$ 中的点,那么不在同一个连通块里的点就不能够互相到达,这个圆点就是合法的。
显然需要建出圆方树的虚树。观察下图,为 $\{2,7,10\}$ 对应的虚树:
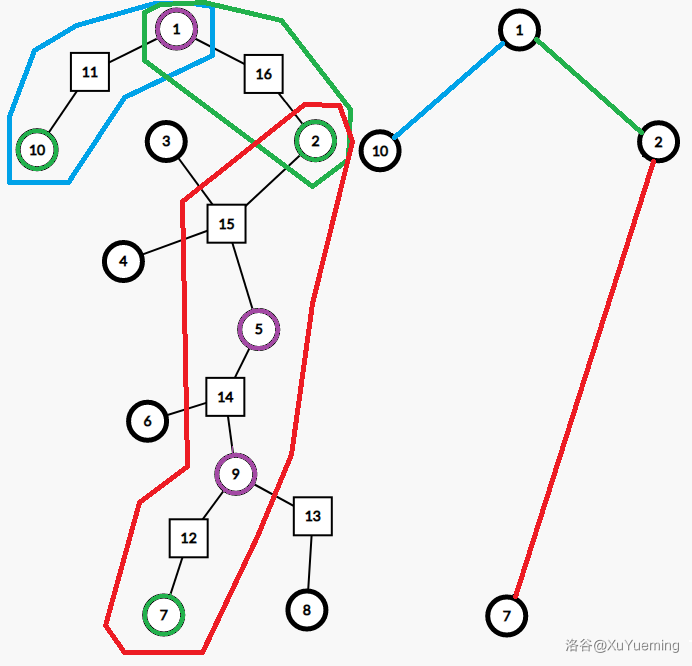
其中紫色圈出来的点表示贡献到答案里的点。我们不妨把 $S$ 中的点先看做合法的,最后再减去他们。这样,我们就可以确定哪些圆点需要贡献到答案中去了。对于一条虚树上的树边 $(u,v)$,圆方树上 $u\rightarrow v$ 这条简单路径上的所有圆点都是合法的。正确性也十分显然。计数的话只需要做一遍树上前缀和就能单次 $\mathcal{O}(1)$ 求出路径上有多少圆点。端点可能会重复统计?只需要在统计时,不统计父亲即可,因为父亲会恰好作为一次孩子被统计到,当然,除了根,那么最后看一下根是不是一个圆点即可。
时间复杂度 $\mathcal{O}(m+n\log n+\sum|S|\log|S|)$。
或者可以离线下来,配合 $\mathcal{O}(n)\sim\mathcal{O}(1)$ LCA,做到 $\mathcal{O}(|S|)$ 建立虚树,总的时间复杂度是线性 $\mathcal{O}(m+n+\sum|S|)$。
**Solution:**
见[博客](https://www.cnblogs.com/XuYueming/p/18313014)。
## 其他想讲的题目
**例十五、同一点双?:**
**Problem Statement:**
给你一个有 $n$ 个点和 $m$ 条边的无向图,和 $q$ 组询问,每次询问两点 $u,v$ 是否在同一点双内。
$n\leq 10^5$,$m\leq 10^6$,$q\leq 10^6$。
**Problem Analysis:**
在经历了种种难题的洗礼,这一题就显得十分简单了。
两个点在同一个点双中,当且仅当存在一个连接他们的方点。
分类讨论可知,情况只有两种:其中一个是另一个的爷爷、其中一个是另一个的兄弟。前一种情况对应于一个是方点的父亲,一个是方点的孩子;后一种情况对应于两个都是方点的孩子。
于是每次可以 $\mathcal{O}(1)$ 判断。
------
之所以有这一道水题,是因为[《POI1999 Store-keeper 题解》](https://www.cnblogs.com/XuYueming/p/18285675)中,本人采用「用来弹栈的割点」来理解此问题。事实上,在学习圆方树后,可以更清晰地理解这个问题:最终我们标记出来每个点所属的点双,和其在圆方树上的父亲是等价的。「用来弹栈的割点」便是方点的父亲圆点。
## 总结
通过本文的学习,我们深入探讨了圆方树这一结构在图论问题中的建模价值,特别是在仙人掌图及一般无向图中的实践应用。我们探究了树形 DP、点分治、树上启发式合并(DSU on tree)、树链剖分、虚树、动态 DP(DDP)、动态树等多种算法技巧,在这些图结构上的适用性和实现方法。同时,我们也厘清了一个核心问题:如何在这些图中高效维护**点对之间所有简单路径的信息**,从而为我们提供一种解决问题的全新的视角。
## 习题
这里总结了一些习题,大家可以练练手。
1. 例一、静态仙人掌最大独立集(小 C 的独立集,link、link、link)
1. 例二、静态仙人掌直径([SHOI2008] 仙人掌图,link、link、link)
1. 例三、persistent DSU on cactus(link)
1. 例四、GAME on cactus(link)
1. 例五、仙人掌点对间最短路长度(【模板】静态仙人掌,link)
1. 例六、BUY on cactus(link)
1. 例七、【清华集训2015】静态仙人掌(link)
1. 例八、mx 的仙人掌(link)
1. 例九、【集训队互测2016】火车司机出秦川(link)
1. 例十、DDP on cactus(link)
1. 例十一、[APIO2018] 铁人两项(link)
1. 例十二、必经点个数(link,link,link)
1. 例十三、[ZJOI2022] 简单题(link、link)
1. 例十四、Tourists(link)
1. 例十五、[SDOI2018] 战略游戏(link)
欢迎补充。
## 编辑历史
- 2024-7-21:初版发布。
- 2025-3-19:开始重构。
- 2025-5-4:完成初稿。
- 2025-6-7:进一步整理重写,完成二稿。
- 2025-6-13:完成语言润色。
- 2025-7-19:学考后继续完善。新增仙人掌上换根 DP。
- 2025-7-19:检查审稿,发布终稿,投稿博客园首页。
## 原版博客
略