题解:P10874 [COTS/CETS 2022] 旅程 Dugput(民间数据)
Otomachi_Una_
·
·
题解
【鸣谢】
感谢树姐姐给予思路的启发。
【题目简述】
在 n\times m 的方格中找到 (x_1,y_1) 到 (x_2,y_2) 的最长路。
对于部分测试点只需要输出长度。
**【解题思路】**
先来解决 $type=1$ 的问题。下面提到答案指最长路的长度。
我们不妨假设 $n\leq m$,$x_1\leq x_2$,$y_1\leq y_2$。
直觉告诉我们在大多数情况下,答案直接黑白染色分析奇偶就出来了。
我们打个表,把不满足黑白染色规律的 $(n,m,x_1,y_1,x_2,y_2)$ 找出来。
我们发现这些不符合条件的都满足 $n\leq 3$。我们来分类讨论一下:
- 当 $n=1$,答案显然是 $y_2-y_1$。
- 当 $n=2$,如果 $x_1=1,x_2=2$ 且 $y_2-y_1\leq 1$。那么此时 $(x_1,y_1),(x_2,y_2)$ 把整个格子分割成两部分,取最大的一边即可。
- 当 $n=3$,这时情况比较多。但是仔细观察都能发现此时不符合的 $m$ 必然为偶数。这里需要读者自己打表找规律。或者见下面的代码。下图呈现了几种可能的不合法情况。
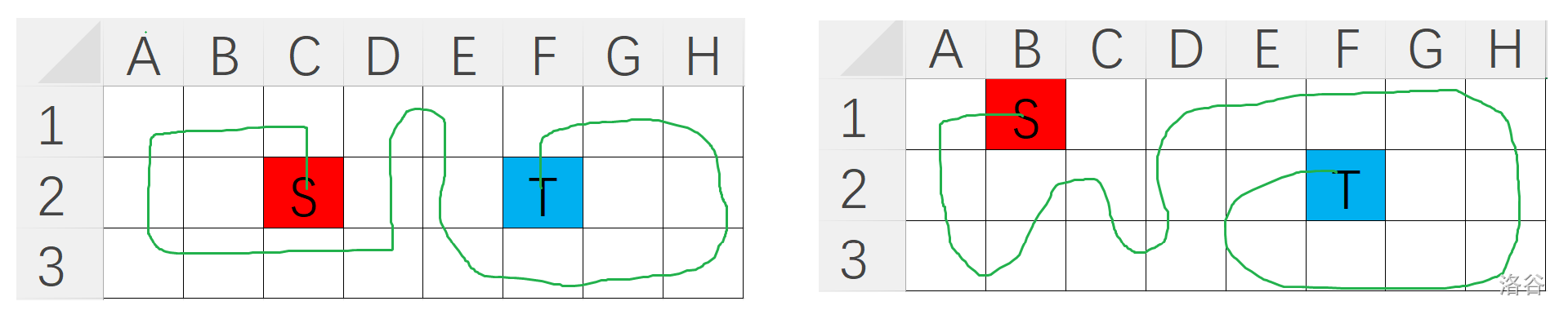
在完成对 $type=1$ 的问题之后,我们可以进行递归了。下图是一种容易想到的递归方式:
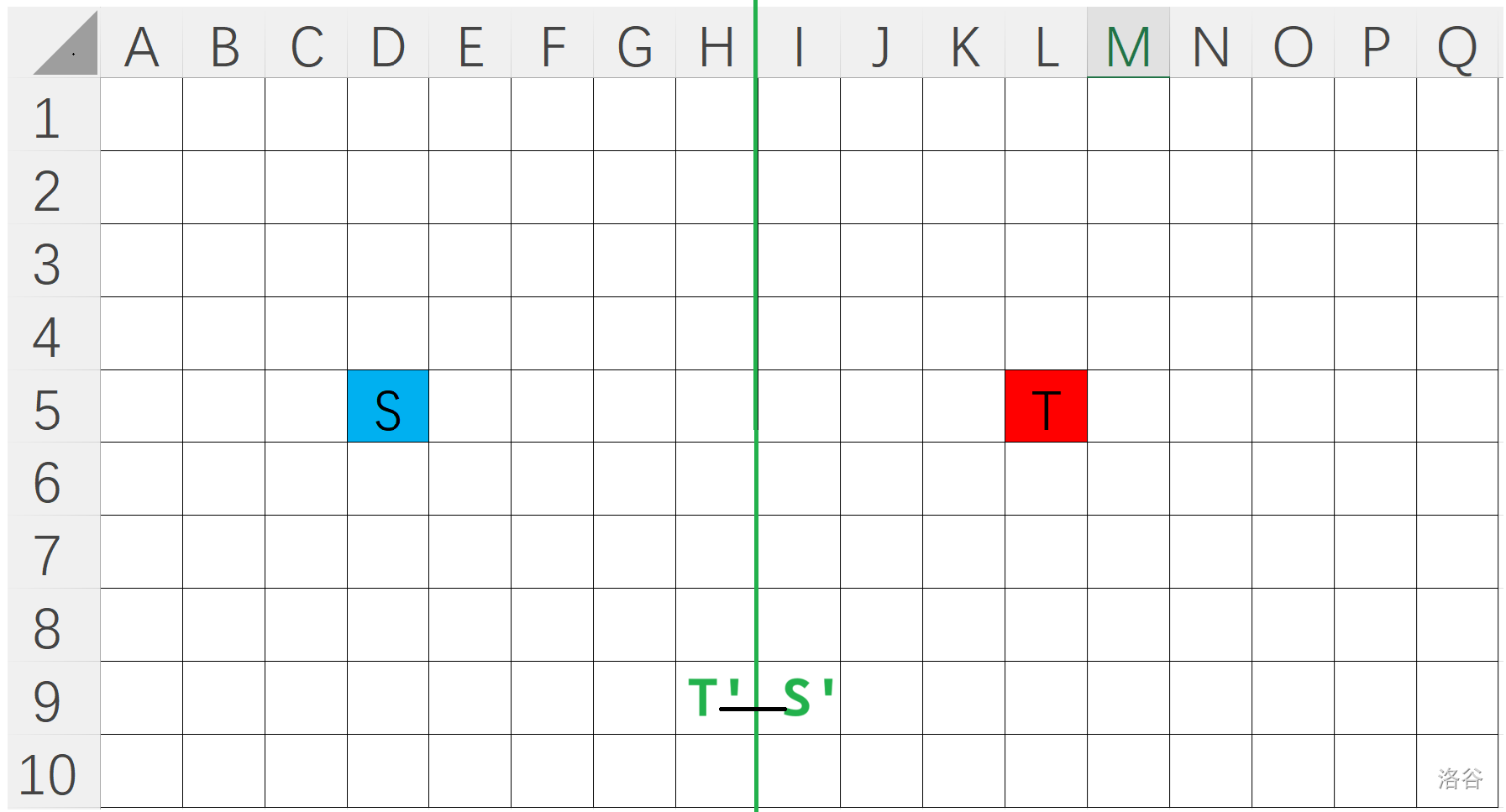
我们以绿色线为分割线,先把左边 $S\to T'$ 再到 $S'\to T$。
如果我们两边最大步数的和恰好为我原图的最大步数,我们便完成可递归。
上面是对 $y$ 的分割,对 $x$ 的分割同理。
此时仍然有部分情况没有被成功分治,我们打表,来一一攻破。
首先是 $n=3$ 的情况。通过打表,发现这类情况总有 $y_2-y_1\leq 1$。分类讨论一下就行了。
剩下的情况总满足 $x_1=x_2$ 或者 $y_1=y_2$。不妨让 $y_1=y_2$。我们人类智慧地再来进行分治:
下面列出了 $4$ 种可能分治的情况,实际上对称一下一共有 $8$ 种。
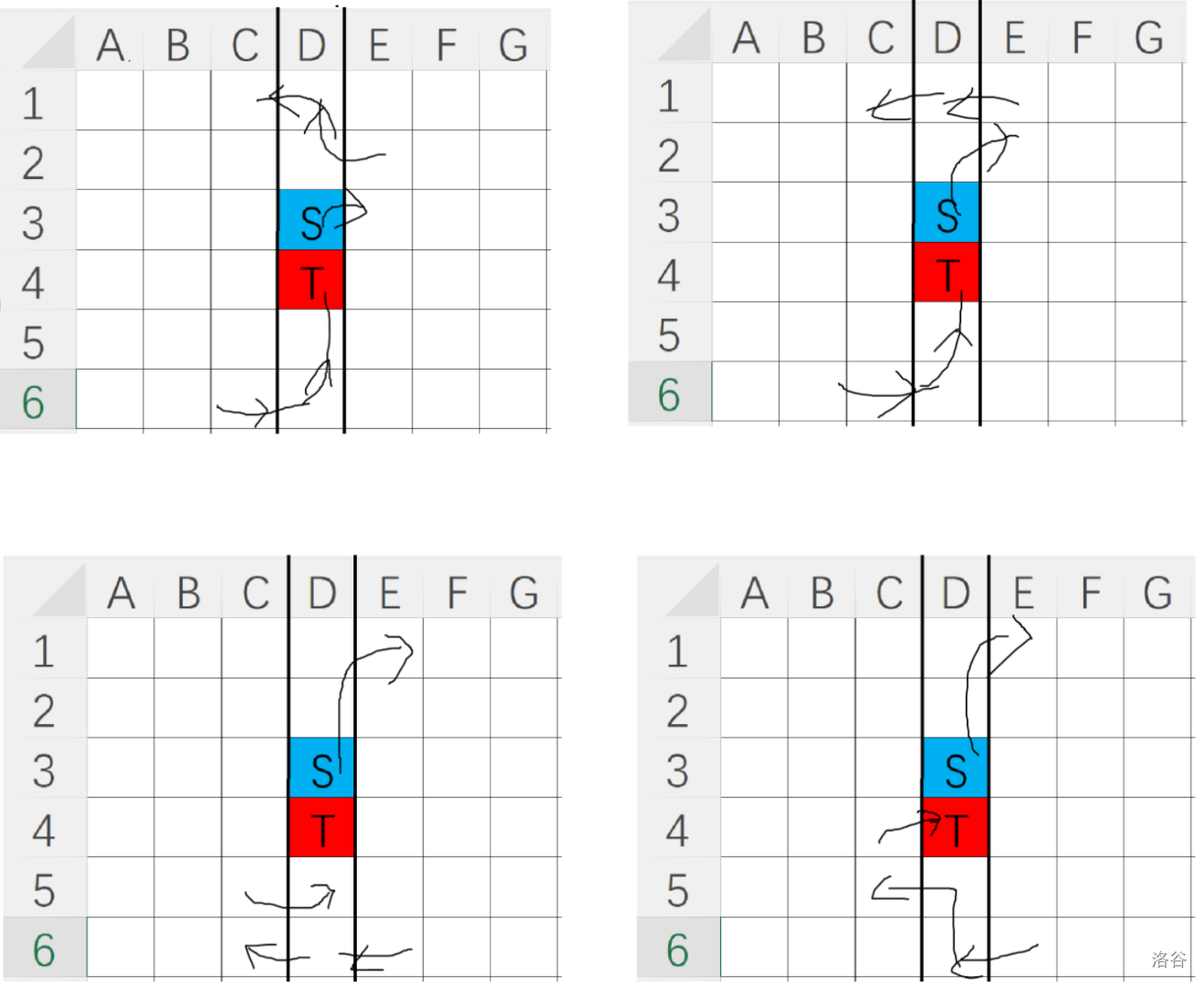
讨论完这几种情况你就发现没有分治不了的东西了。完结撒花~
**【参考代码】**
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define MP make_pair
mt19937 rnd(time(0));
const int MAXN=5005;
int tid,T;
bool ri[MAXN][MAXN],dw[MAXN][MAXN];
bool vis[MAXN][MAXN];
map<array<int,6>,string> mp;
int max_len(int n,int m,int x1,int y1,int x2,int y2){
if(x1==x2&&y1==y2) return 1;
if(n>m) return max_len(m,n,y1,x1,y2,x2);
if(x1>x2) return max_len(n,m,n+1-x1,y1,n+1-x2,y2);
if(y1>y2) return max_len(n,m,x1,m+1-y1,x2,m+1-y2);
if(n==1) return y2-y1+1;
if(n==2&&x2-x1==1&&y2-y1<=1) return max(y1+y2,2*m+2-y1-y2);
if(n*m&1) return n*m-((x1+y1)&1)-((x2+y2)&1);
if(n==3&&((x1+x2+y1+y2)&1)&&((y2-y1>=2&&((x1+y1)&1))||(x1==2&&x2==2&&(y1&1)))) return n*m-2;
return n*m-(~(x1+x2+y1+y2)&1);
}
string replace(string s,char L,char R,char U,char D){
for(int i=0;i<s.length();i++){
if(s[i]=='L') s[i]=L;
else if(s[i]=='R') s[i]=R;
else if(s[i]=='U') s[i]=U;
else if(s[i]=='D') s[i]=D;
}
return s;
}
string rev(string s){
reverse(s.begin(),s.end());
return replace(s,'R','L','D','U');
}
string solve(int n,int m,int x1,int y1,int x2,int y2){
if(x1==x2&&y1==y2) return (string){};
if(mp.count({n,m,x1,y1,x2,y2})) return mp[{n,m,x1,y1,x2,y2}];
if(n>m) return replace(solve(m,n,y1,x1,y2,x2),'U','D','L','R');
if(x1>x2) return replace(solve(n,m,n+1-x1,y1,n+1-x2,y2),'L','R','D','U');
if(y1>y2) return replace(solve(n,m,x1,m+1-y1,x2,m+1-y2),'R','L','U','D');
if(n==1) return string(y2-y1,'R');
int C=max_len(n,m,x1,y1,x2,y2);
for(int x=1;x<=n;x++) if(x1<=x&&x<x2) for(int y=1;y<=m;y++){
if(C==max_len(x,m,x1,y1,x,y)+max_len(n-x,m,1,y,x2-x,y2)){
return mp[{n,m,x1,y1,x2,y2}]=solve(x,m,x1,y1,x,y)+"D"+solve(n-x,m,1,y,x2-x,y2);
}
}
for(int y=1;y<=m;y++) if(y1<=y&&y<y2) for(int x=1;x<=n;x++){
if(C==max_len(n,y,x1,y1,x,y)+max_len(n,m-y,x,1,x2,y2-y)){
return mp[{n,m,x1,y1,x2,y2}]=solve(n,y,x1,y1,x,y)+"R"+solve(n,m-y,x,1,x2,y2-y);
}
}
if(n==3&&y1==y2){
int x3=6-x1-x2;
if(3+max_len(3,y1-1,x1,y1-1,x3,y1-1)+max_len(3,m-y1,x3,1,x2,1)==C){
return mp[{n,m,x1,y1,x2,y2}]="L"+solve(3,y1-1,x1,y1-1,x3,y1-1)+"RR"+
solve(3,m-y1,x3,1,x2,1)+"L";
}
if(3+max_len(3,m-y1,x1,1,x3,1)+max_len(3,y1-1,x3,y1-1,x2,y1-1)==C){
return mp[{n,m,x1,y1,x2,y2}]="R"+solve(3,m-y1,x1,1,x3,1)+"LL"+
solve(3,y1-1,x3,y1-1,x2,y1-1)+"R";
}
}else if(n==3&&y2-y1==1){
assert(x1==1&&x2==3);
if(6+max_len(3,m-y2,1,1,2,1)+max_len(3,y1-1,2,y1-1,3,y1-1)==C)
return mp[{n,m,x1,y1,x2,y2}]="RR"+solve(3,m-y2,1,1,2,1)+"LLL"+
solve(3,y1-1,2,y1-1,3,y1-1)+"RR";
}
bool flag=(x1==x2);string s;
if(flag) swap(n,m),swap(x1,y1),swap(x2,y2);
for(int o:{0,1}){
for(int i=x2+1;i<=n;i++){
if(n+max_len(n,m-y1,1,1,i,1)+max_len(n,y1-1,n,y1-1,i-1,y1-1)==C){
s=string(x1-1,'U')+"R"+solve(n,m-y1,1,1,i,1)+"L"+string(n-i,'D')+"L"+
solve(n,y1-1,n,y1-1,i-1,y1-1)+"R"+string(i-1-x2,'U');
if(o) s=replace(s,'R','L','U','D');
if(!flag) return mp[{n,m,x1,y1,x2,y2}]=s;
return mp[{n,m,x1,y1,x2,y2}]=replace(s,'U','D','L','R');
}else if(n+max_len(n,m-y1,1,1,n,1)+max_len(n,y1-1,i,y1-1,i-1,y1-1)==C){
s=string(x1-1,'U')+"R"+solve(n,m-y1,1,1,n,1)+"L"+string(n-i,'U')+"L"+
solve(n,y1-1,i,y1-1,i-1,y1-1)+"R"+string(i-1-x2,'U');
if(o) s=replace(s,'R','L','U','D');
if(!flag) return mp[{n,m,x1,y1,x2,y2}]=s;
return mp[{n,m,x1,y1,x2,y2}]=replace(s,'U','D','L','R');
}
}
for(int i=1;i<x1;i++){
if(n+max_len(n,m-y1,i+1,1,i,1)+max_len(n,y1-1,1,y1-1,n,y1-1)==C){
s=string(x1-i-1,'U')+"R"+solve(n,m-y1,i+1,1,i,1)+"L"+string(i-1,'U')+"L"+
solve(n,y1-1,1,y1-1,n,y1-1)+"R"+string(n-x2,'U');
if(o) s=replace(s,'R','L','U','D');
if(!flag) return mp[{n,m,x1,y1,x2,y2}]=s;
return mp[{n,m,x1,y1,x2,y2}]=replace(s,'U','D','L','R');
}else if(n+max_len(n,m-y1,i+1,1,1,1)+max_len(n,y1-1,i,y1-1,n,y1-1)==C){
s=string(x1-i-1,'U')+"R"+solve(n,m-y1,i+1,1,1,1)+"L"+string(i-1,'D')+
"L"+solve(n,y1-1,i,y1-1,n,y1-1)+"R"+string(n-x2,'U');
if(o) s=replace(s,'R','L','U','D');
if(!flag) return mp[{n,m,x1,y1,x2,y2}]=s;
return mp[{n,m,x1,y1,x2,y2}]=replace(s,'U','D','L','R');
}
}
y1=y2=m+1-y1;
}
assert(0);
}
int main(){
ios::sync_with_stdio(false);
// freopen("Otomachi_Una.in","r",stdin);
// freopen("Otomachi_Una.out","w",stdout);
cin>>tid>>T;
while(T--){
int n,m,x1,y1,x2,y2;
cin>>n>>m>>x1>>y1>>x2>>y2;
if(tid) cout<<max_len(n,m,x1,y1,x2,y2)<<'\n';
else{
string s=solve(n,m,x1,y1,x2,y2);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) vis[i][j]=ri[i][j]=dw[i][j]=0;
int x=x1,y=y1;
for(char c:s){
vis[x][y]=true;
if(c=='L'){
ri[x][--y]=true;
}else if(c=='R'){
ri[x][y++]=true;
}else if(c=='U'){
dw[--x][y]=true;
}else{
dw[x++][y]=true;
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cout<<"o*"[(i==x1&&j==y1)||(i==x2&&j==y2)];
if(j<m) for(int o:{0,1}) cout<<" -"[ri[i][j]];
}
cout<<'\n';
if(i<n){
for(int j=1;j<=m;j++){
cout<<" |"[dw[i][j]];
if(j<m) cout<<" ";
}
cout<<'\n';
}
}
}
}
cerr<<"Running time: "<<1.*clock()/CLOCKS_PER_SEC<<'\n';
return 0;
}
```