算不算 OI/IOI 赛制的独有魅力?
Loop1st
·
·
算法·理论
Part 1 前言
烂活,去年某个人 NOIP 前写了 NOIP 题解然后拿了 ZJ 最低分,是谁呢好难猜啊
在各类正赛/模拟赛的赛场上,我们时常可以看到一些题目有一些特殊性质,根据这些性质,我们可以更好地想到正解。
为什么这类题经常出现呢?笔者认为一是出题人需要设立有梯度的数据,使得比赛尽量有区分度,二是出题人想让自己辛苦出的题有尽量多的人过,就给了特殊性质来启发正解。也就是说,出题人希望你的做题流程是:看题,想特殊性质的部分分,根据部分分求出正解。综上,根据特殊性质做题的能力是极为重要的。
Part 2 根据已有性质直接思考
树上问题
[CSP-S2019] 括号树
先考虑链的做法,发现开个栈就没了,然后树的做法就是访问一个点的时候入栈,递归完所有子节点后出栈。
[CSP-S2019] 树上的数
著名的 @A_zjzj 曾经说过,他造树的题都会加链和菊花的部分分,如果两个都会了,就有很大概率会这道题了。然而他讲的那节课我只记得这句话了。
首先枚举当前数字。
考虑菊花图怎么做。我们发现将删的边按顺序连一起,发现每次在中心节点上的数字就构成了一个环,用并查集贪心地维护即可。
然后是链。我们发现一个节点最后的数字从哪边来取决于先删左边还是先删右边,对于每个点记一个优先级即可。具体可以画图理解。
受上述启发得到正解:考虑枚举数字 k,经过的点依次为 u_1, u_2, \cdots, u_m,那么有以下三个要求:
-
-
- 对于 i \in [2, m - 1],在 u_i 的所有边中 (u_i, u_{i + 1}) 紧接在 (u_{i - 1}, u_i) 之后删除。
有了这个,仿照菊花图,对每个点开一个并查集,维护优先级,优先级大的是优先级小的祖先,一条边的父亲节点表示对于其和其父亲的公共节点 u,在与 u 相邻的所有边中,这两条边的删除顺序是紧挨着的,即其父亲删完后马上删这条。
这里推荐链式前向星存图,方便记边的编号。
注意代码里只开了一个并查集,但是每个点连的边之间是独立的(一条边被拆成了两条有向的)。虚点的意思是,对于一个点连出去的所有边,虚点向最早删除的边连边,最迟删除的边向虚点连边,作用是能让每个点的并查集最后形成一个环,更方便维护信息。
时间复杂度 \mathcal{O}(n^2)。因为链的并查集均摊线性。
[CSP-S 2022] 数据传输
其实这题有点牵强了()。但是 k = 1, k = 2 你就说是不是特殊性质罢!
$k = 2$ 我们需要手玩,发现不会走出树上两点路径,然后就是一个简单的 dp,列出矩阵就过了。
然后我们就要拓展到 $k = 3$,发现这时候是可以走出树上两点路径的,并且距离不能超过 $2$,其实由于 $k = 2$ 的存在,列出这个 dp 的矩阵是比较简单的。
$$[dp_j,dp_{j-1},dp_{j-2}] \times \begin{bmatrix}v_i&0&+\infty\\v_i&w_i&0\\v_i&+\infty&+\infty\end{bmatrix}=[dp_i,dp_{i-1},dp_{i-2}]$$
(不会打 LaTeX 随便扒了一个下来 QwQ)
其中 $dp_{i-k}$ 是指在距离树上节点 $i$ 为 $k$ 的点上的答案。
后面就是树剖倍增并查集各显神通的动态 DP 环节。
## 其它题
### [[NOISG 2023 Qualification] Dolls](https://www.luogu.com.cn/problem/P10729)
$a_i$ 是奇数,我们可以发现一个数只要之前没出现过就有贡献。
$a_i$ 不是 $4$ 的倍数,考虑在数轴上,一个数出现过就填 $1$ 否则填 $0$ 那么最后肯定是这样的:
$$0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0$$
发现由若干个连续 $1$ 和 $0$ 组成,且连续的 $1$ 组成的段之间是独立的,可以直接加起来。对于长度为 $l$ 的连续 $1$ 段,贡献是 $\lceil\frac{l}{2}\rceil$,由于 $a_i$ 不是 $4$ 的倍数,一段最长是 $4$,枚举新加进来的周围的段即可。
对于正解,发现加进来一个数就是合并两边的段(如果有的话),查询的是段的大小,使用并查集就能维护了。
### [[ROI 2017] 存储器 (Day 2)](https://www.luogu.com.cn/problem/P10653)
观察特殊性质:串 $T$ 全是 `+`,说明只需要把 $S$ 中的 `-` 都消去,使用链表模拟是 $\mathcal{O}(n^2)$ 的,但是如果成功消去一段之后马上回退到上一段,就能保证复杂度是线性的,因为每次只会执行合并,往后跳,不动三种情况。
这个特殊性质会做了,整道题就会做了,将 $T$ 划分成若干极长的段,如果这段是 `-` 就让对应的 $S$ 变成全 `-`,反之同理,然后加上一些特判,因为如果一开始一段是相同的话,是不能分裂的,其次首尾是必须和 $T$ 这一段相同的,不然会和上一段 $S$ 拼在一起。
### [[NOIP2023] 双序列拓展](https://www.luogu.com.cn/problem/P9870)
首先明白题目的限制条件就是 $\forall 1 \le i \ge 10^{100} \land f_i > g_i$ 或 $\forall 1 \le i \ge 10^{100} \land f_i < g_i$,两边只要判断一边即可,另一边只需要 $x, y, n, m$ 互换再判断即可。
我们来考虑前者,还是可以转化成图论问题思考:
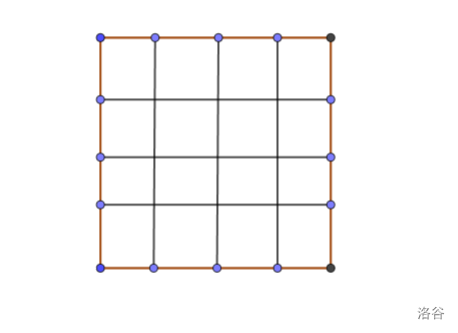
如图,横坐标表示当前匹配到的是 $X_i$,纵坐标表示当前匹配的是 $Y_i$。
题目相当于是说我们当前匹配到了 $(1, 1)$(若 $X_1 \ge Y_1$ 就直接倒闭了),要走到 $(n, m)$(即匹配完所有),是否可行,每次匹配,如果匹配到了 $(i, j)$,若 $X_i<Y_{i+1}$,则可以走到 $(i,j+1)$,$X_{i+1}<Y_i$,则可以走到 $(i+1,j)$,$X_{i+1}<Y_{i+1}$,则可以走到 $(i+1,j+1)$。形式化地,记 $A_{i, j}=[X_i < Y_i]$,若走到了 $(i, j)$,且 $A_{i+0/1,j+0/1} = 1$,则可以走到 $(i+0/1,j+0/1)$。
直接暴力走是 $\mathcal{O}(nmq)$ 的,接下来考虑优化。
看到特殊性质产生联想,容易发现如果 $X_{\min} \le Y_{\min}$,则 $Y_{\min}$ 这行都是 $0$,是无解的。同理如果 $X_{\max} \ge Y_{\max}$,那么 $X_{\max}$ 这列都是 $0$,也无解。
如果过了以上特判,那么特殊性质的图就有了一个强大的性质:
$\forall 1 \le i \ge m, A_{n,i} = 1
\forall 1 \le i \ge n, A_{i, m} = 1
那么图上就多了两条线,线上的点都是 1。如图所示
此时由于我们的目的是走到 (n,m),而走到线上任意一个点都可以走到 (n,m),所以我们只要走到线上即可,又有走到第 n-1 列或第 m-1 行就能走到线上,所以题目的要求缩小成了走到第 n-1 列或第 m-1 行。
由特殊性质的启发,我们想到去寻找这两条线,然后判断是否能从 (1, 1) 走到线上,并从线上走到 (n, m) 即可,那么就是递归求解,每次寻找前缀/后缀最大值的位置就行了,并且这样肯定是更优的。
时间复杂度 \mathcal{O}((n+m)q).
[NOI2022] 冒泡排序
记得到的序列为 a。
首先是必须得到的性质:
存在一种最优方案,使得 \forall a_i, \exists j \space s.t. \space V_j=a_i。证明:考虑如果不是,从后往前调整:将 a_i 变为最小的 V_j 使调整后不违反限制,这样不会增加逆序对。
对于每个特殊性质考虑:
B. 相当于是单点赋值,其它位置任选,发现其它位置一定会填成非降的,因为如果任选的位置有逆序对,交换这两个数。然后记 c_v 表示当前位置填 v 的贡献,从后往前考虑,如果一个位置任意填,就填成 \argmin c_j,如果不任意填,就将 c_1 ~ c_{a_i - 1} 区间减一,其余加一,用线段树维护即可。
C. 显然每个区间让 a_{L_i}=V_i 最优,如果不是,交换 V_i 的位置和 a_{L_i}。然后同样的使用线段树,但是记一个 low_i 表示 a_i 至少填多少,然后 \argmin 里面多了个下界。
如果是从后往前填,如何考虑 i 前面的数的贡献?我们直接假设 i 前面的数如果有 low,填的全部是 low,因为感性理解的话,前面的数选的越小对后面的数影响越小,证明的话,如果后来发现某个 j < i,a_j \neq low_j,那么直接让后面在 [low_j, a_j] 之间的数变成 a_j 即可。
A. 对于 V_i 等于 1 的区间全部都是 1,V_i=0 的区间全部拎出来,从后往前考虑,当且仅当填 1 会不合法时填 0。
那么从小到大考虑每个 V,对区间的 L 降序排序,然后对于每个限制,已经钦定的位置能否满足这个限制,如果不能,从所有 low_i = V 的 i 中找,找不到就无解,否则钦定最小的 i 为 V,因为小的数填前面更优。这个过程可以用 set 维护。
正解:先求出 low,再类似 A 性质弄出单点的限制。最后只需要从大到小枚举 k 并处理所有 V_i=k 的限制,使用线段树维护。树状数组统计答案。
时间复杂度 \mathcal{O}(n \log n)。
Part 3 弱化/创造一下限制
如果这个限制弱化了会咋样?
[COCI 2018/2019 #3] Sajam
观察这个性质:k < \dfrac{n}{2} 有啥用?如果改成 k < n,我们可以使用鸽巢原理得出一些结论,详见我的题解。
创造性质
这类题很多了,你需要自己想一个性质而不是依靠出题人给出,然后看看有没有启发。(其实说白了就是猜结论)。
来举个例子:
[CSP-S2020] 贪吃蛇
如果我给你两个性质:
- 对于每条蛇,保证它吃完之后不会变成最弱的蛇(30pts)
- 对于每条蛇,保证它吃完之后会变成最弱的蛇(30pts)
考虑性质 1 进行分讨:
- 如果这条蛇吃完之后还是最强的,那么肯定会吃
- 如果不是最强的也不是最弱的,那么下一轮是次强的决策,且这时候最弱的变为了原先次弱的,所以如果次强蛇吃了,次强蛇就会比最强蛇小,如果最强蛇死了,那么次强蛇必定先死,由于次强蛇能够决策,所以它肯定不会死,所以最强蛇也不会死。
考虑性质 2:
假设现在开始每条决策的蛇是 1, 2, 3, \cdots, k,如果 1 吃了之后变成了最弱的,由 2 决策,如果 2 吃了 1 不是最弱的,那根据第二点,1 会死,1 知道这点,不会吃。否则,2 需要看 3 来决定吃不吃,如果 2 会吃 1,1 就会选择结束,否则 1 会吃,对于 2 也同理,同时 3 需要依赖 4,以此类推,如果只剩两条蛇了,那么当前决策的蛇肯定不敢吃,不然会被最后一条吃掉,所以我们发现如果 k 是奇数就会吃。并且吃了之后 2 也不会吃了,因为 2 变成了新的 1,k 变成了偶数,所以一旦出现这种情况,最多再吃一次了。
然后你发现性质 1,2 一结合,用 set 随便拿到 70pts。并且性质 1 的第二种情况告诉我们蛇吃完之后的长度是不增的,所以可以直接开俩队列维护,就过了。
[CCO 2020] Shopping Plans
矮油味题目给的性质一点用都没有,我来给三个:
-
-
-
这道题以及 [eJOI 2025] Navigation 留作练习。
Part 4 总结
这类题目首先需要转化好题意,了解这个性质的用意。性质可以帮忙推出结论,可以帮忙创造子问题,很有区分度,能精准区分我这样的飞舞。
Part 5 所有代码实现带注释:
link
参考文献: