P10894
YQsunny
·
·
题解
虚树
题目大意
给出一棵树,设点集为 S。
有多次询问,每次询问切除一棵子树,求剩下的树中所有满足条件的非空子集的方案数。
把这个题换成人话就是选出来一些点,对于任意的两个点,它们的 $\operatorname{LCA}$ 也在这些选出来的点里面,求其方案数。
### 设计状态
碰到这种树上计数问题,首先就想到树形 dp 来求解。
不难想到状态需要枚举 $\operatorname{LCA}$ 来实现,发现在统计以节点 $i$ 为根的子树时,在节点 $i$ 的不同的子树中的两个点,都是以节点 $i$ 为 $\operatorname{LCA}$ 的,而在相同子树内的两个点,那么便可以递归到它们的 $\operatorname{LCA}$ 接着求解。
所以用 $f_i$ 表示以 $i$ 为根的子树中满足条件的方案数。
### 初始化
首先来看题目中有 $\operatorname{LCA}$,那么就肯定与 $\operatorname{LCA}$ 有关。(~~这不是废话吗~~)
那么考虑如何不重不漏的统计一个节点的方案数。
注意到每个点只有两种状态(选或不选),那么处理到节点 $i$ 的时候,完全可以将这两种状态分别计入答案。
每个点单独选出来便是一个答案,那么每个节点初始方案数为 $1$。
### 状态转移
#### 不选的情况
容易发现当不选节点 $i$ 时,在 $i$ 的不同子树的答案是永远不能合并的,因为 $i$ 的不同子树内的两个点,他们的 $\operatorname{LCA}$ 永远是 $i$。
如果不选这个节点,强行选择不同子树内的两个点,那么就不满足它们的 最近公共祖先在点集里了,所以只需要将每个子树内的方案数相加即可。
用 $\operatorname{son}_i$ 表示节点 $i$ 的儿子。
所以有 $f_i = \sum_{to\in\operatorname{son}_i} f_{to}$。
这部分代码如下。
```cpp
void dfs(int x,int fa){
f[x]=1;
for(int i=head[x];i;i=e[i].next){
int to=e[i].to;
if(to==fa)
continue;
dfs(to,x);
f[x]+=f[to];
}
}
```
#### 选的情况
当选择节点 $i$ 时,那么就需要合并节点 $i$ 的不同子树内的方案数。
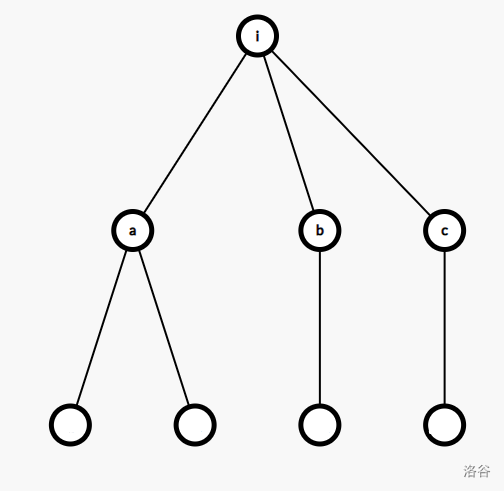
因为已经选了 $i$ 这个点,所以任意几棵子树的答案都是可以合并的,如上图,根据乘法原理和加法原理,节点 $i$ 有三棵分别以 $a,b,c$ 为根的子树,那么 $f_a , f_b, f_c , f_a \times f_b,f_a \times f_c ,f_b \times f_c ,f_a \times f_b \times f_c$ 都应该作为答案累计计入 $f_i$ 中。
我们发现如果这样算的话,算一个节点的时间复杂度是 $\mathcal{O(n^2)}$,需要找出一个 $\mathcal{O(1)}$ 的式子来计算。
假设有四个节点 $a,b,c,d$,不难发现它们的方案数其实就是 $(f_a+1)(f_b+1)(f_c+1)(f_d+1)-1$。
所以有 $f_i = \prod_{to\in \operatorname{son}_i}^{} \ (f_{to}+1)-1$。
这部分代码如下。
```
void dfs(int x,int fa){
f[x]=1;
for(int i=head[x];i;i=e[i].next){
int to=e[i].to;
if(to==fa)
continue;
dfs(to,x);
f[x]*=(f[to]+1);
}
f[x]--;
}
```
最后整理一下式子。
$$
f_i = \prod_{to\in \operatorname{son}_i}(f_{to}+1)+ \sum_{to\in \operatorname{son}_i}f_{to}
$$
暴力代码,每次更改时将切掉的子树打上标记,不去经过它,然后重新求一遍答案。
### 代码
#### 30pts
```
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
#define int long long
const int N=5e5+10,mod=998244353,inf=1e9;
int n,m,f[N],fa[N],head[N],pos=0;
inline int read(){
char c=getchar();int x=0,f=1;
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
struct mm{
int to,next;
}e[2*N];
bool vis[N];
void add(int x,int y){
pos++;
e[pos].to=y;
e[pos].next=head[x];
head[x]=pos;
}
void dfs(int x,int ff){
fa[x]=ff;
int anss=1;
for(int i=head[x];i;i=e[i].next){
int to=e[i].to;
if(to==ff||vis[to])
continue;
dfs(to,x);
f[x]+=f[to];//当不选i这个点是统计的答案
anss*=(f[to]+1);
anss%=mod;
f[x]%=mod;
}
f[x]+=anss;
f[x]=(f[x]+mod)%mod;
}
signed main(){
n=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v);
add(v,u);
}
m=read();
for(int i=1;i<=m;i++){
int x=read();
for(int j=1;j<=n;j++)
f[j]=1;
vis[x]=1;
dfs(1,0);
cout<<f[1]<<endl;
vis[x]=0;
}
return 0;
}
```
时间复杂度为 $\mathcal{O(nm)}$。
#### 100pts
发现要想不超时,那么就必须预处理某些东西来降低时间复杂度。
考虑每个节点 $u$ 对于它的父亲 $i$ 的贡献为
$$
f_u \times (\prod_{to\in \operatorname{bro}_{u}}^{} \ (f_{to}+1) +1 )
$$
($\operatorname{bro}_{u}$ 为节点 $u$ 的兄弟节点)。
这部分代码如下。
```
void dfs(int x,int fa){
sum[x]=1;//连乘数组
int anss=1;
for(int i=head[x];i;i=e[i].next){
int to=e[i].to;
if(to==fa)
continue;
dfs(to,x);
sum[x]=(sum[x]*(f[to]+1))%mod;
}
for(int i=head[x];i;i=e[i].next){
int to=e[i].to;
if(e[i].to!=fa){
int to=e[i].to;
g[to]=(sum[x]*ksm(f[to]+1,mod-2)+1)%mod;
}
}
}
```
$g_{i}$ 表示节点 $i$ 对于父亲的贡献,那么接下来只需要一个前缀积便可 $\mathcal{O(1)}$ 计算出答案,那么假设切掉以节点 $u$ 为根的子树,答案即为 $f_{u} - f_x \times g_{u}$。
时间复杂度为 $\mathcal{O(n+m)}$。
代码如下。
```
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
#define int long long
const int N=5e5+10,mod=998244353,inf=1e9;
int n,m,f[N],fa[N],head[N],pos=0,g[N],sum[N];
inline int read(){
char c=getchar();int x=0,f=1;
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
struct mm{
int to,next;
}e[2*N];
int ksm(int x,int b){
int anss=1;
while(b){
if(b&1)
anss*=x,anss%=mod;
b>>=1;
x*=x;
x%=mod;
}
return anss;
}
void add(int x,int y){
pos++;
e[pos].to=y;
e[pos].next=head[x];
head[x]=pos;
}
void dfs(int x,int ff){
fa[x]=ff;
sum[x]=1;
for(int i=head[x];i;i=e[i].next){
int to=e[i].to;
if(to==ff)
continue;
dfs(to,x);
f[x]+=f[to];
sum[x]=(sum[x]*(f[to]+1))%mod;;
f[x]%=mod;
}
f[x]+=sum[x];
f[x]=(f[x]+mod)%mod;
for(int i=head[x];i;i=e[i].next)
if(e[i].to!=ff){
int to=e[i].to;
g[to]=(sum[x]*ksm(f[to]+1,mod-2)+1)%mod;
}
}
void dfs2(int x){
if(x>1)
g[x]=g[x]*g[fa[x]]%mod;
for(int i=head[x];i;i=e[i].next){
int to=e[i].to;
if(to==fa[x])
continue;
dfs2(to);
}
}//求出前缀积
signed main(){
n=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v);
add(v,u);
}
m=read();
g[1]=1;
dfs(1,0);
dfs2(1);
for(int i=1;i<=m;i++){
int xx=read();
cout<<(f[1]-g[xx]*f[xx]%mod+mod)%mod<<endl;
}
return 0;
}
```
感谢 @X____ 为我贴心的更改了题解的排版,@mmr123 为我提供了一张图片。