P6755
liuliucy
·
·
题解
各种情况
首先,我们可以用边权表示出每个点的点权:
2a_i=\sum_j e_{i,j}
$$\left\{\begin{matrix}
\sum_j e_{1,j}=2a_1\\
\sum_j e_{2,j}=2a_2\\...
\\
\sum_j e_{n,j}=2a_n
\end{matrix}\right.$$
有 $n$ 个方程,$m$ 个未知数,~~我们用高斯消元暴力~~我们可以知道当 $m>n$ 时方程组有无数组解,图是联通的,所以只可能 $m=n-1$ 或者 $m=n$ ,当 $m=n-1$,这是一棵树,而 $m=n$ 时则是基环树。
我们分别考虑以下三种情况:
如图所示时:
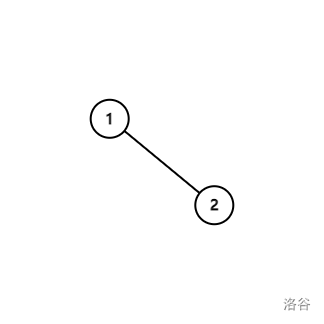
这显然是可以直接算的,因为 $a_1$ 点权的两倍就是 $1-2$ 的边权。
当是个环时:
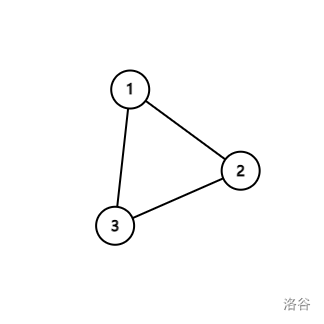
我们可以列出方程组:
$$\left\{\begin{matrix}
e_{1,2}+e_{1,3}=2a_1\\
e_{2,3}+e_{1,2}=2a_2\\
e_{1,3}+e_{2,3}=2a_3
\end{matrix}\right.$$
我们将 $1$ 式减去 $2$ 式 加上 $3$ 式便可得到 $2e_{1,3}$ 的值,之后便可得到所有的边权。
而当环上有偶数个点时:
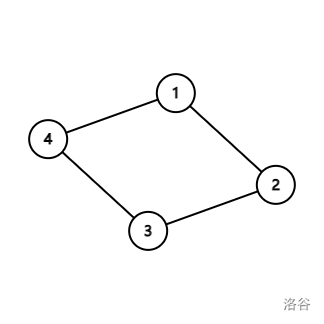
这也有无穷多组解,因为我们将 $e_{1,4}$ 加 $1$ ,$e_{1,2}$ 减 $1$,之后再将 $e_{2,3}$ 加 $1$,$e_{3,4}$ 减 $1$,我们发现这样也是成立的,但是却得到了不同的一组解,所以这样会出现无穷多组解。
## 算法
我们先拓扑排序,先处理掉链的情况,最后只剩下环,最后再处理环即可。
## CODE
```cpp
#include<bits/stdc++.h>
using namespace std;
struct xx{
int x,id,nxt;
}e[1000001];
int head[1000001],cnt;
bool b[1000001];
void add(int x,int y,int id){
e[++cnt].x=y;
e[cnt].id=id;
e[cnt].nxt=head[x];
head[x]=cnt;
}
bool vis[1000001];
bool used[1000001];
int a[1000001],in[10000001];
int ans[10000001];
queue<int>q;
int n,m,aw,ct,f=1;
void dfs1(int x,int fa,int rt){
if(fa!=-1&&rt==x){
if(ct%2==0){
printf("0");
exit(0);
}
return;
}
aw+=f*a[x];
f*=-1;
ct++;
for(int i=head[x];i!=-1;i=e[i].nxt){
int y=e[i].x;
if(y==fa)continue;
if(in[y]<2)continue;
if(b[y])continue;
b[y]=1;
dfs1(y,x,rt);
}
}
void dfs2(int x,int fa,int rt){
if(fa!=-1&&rt==x)return;
for(int i=head[x];i!=-1;i=e[i].nxt){
int y=e[i].x;
if(y==fa)continue;
if(in[y]<2)continue;
if(b[y])continue;
b[y]=1;
aw=a[x]-aw;
ans[e[i].id]=2*aw;
dfs2(y,x,rt);
}
}
signed main(){
memset(head,0xff,sizeof(head));
scanf("%d%d",&n,&m);
if(m>n){
putchar('0');
return 0;
}
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y,i);
add(y,x,i);
in[y]++;in[x]++;
}
for(int i=1;i<=n;i++)if(in[i]==1)q.push(i);
while(!q.empty()){
int x=q.front();
q.pop();
if(used[x])continue;
used[x]=1;
for(int i=head[x];i!=-1;i=e[i].nxt){
int y=e[i].x,id=e[i].id;
if(vis[id])continue;
ans[id]=2*a[x];
a[y]-=a[x];
vis[id]=1;
in[y]--;
if(in[y]==1){
q.push(y);
}
}
}
memset(b,0,sizeof(b));
for(int i=1;i<=n;i++){
if(b[i])continue;
if(in[i]>=2){
dfs1(i,-1,i);
memset(b,0,sizeof(b));
aw/=2;
dfs2(i,-1,i);
}
}
for(int i=1;i<=cnt/2;i++)printf("%d\n",ans[i]);
}
```