题解 SP263 【PERIOD - Period】
辰星凌
·
·
题解
在进入这道题之前,我们先来学习一下 kmp 算法
(如果大佬您已经学习过了,可以直接跳到后面周期性的解释)
术语与规定
为了待会方便,所以不得不做一些看起来很拖沓的术语,但这些规定能让我们更好地理解KMP甚至AC自动机。
字符串匹配形式化定义如下:
假设文本是一个长度为n的数组T[1...n],而模式是一个长度为m的数组P[1...m],其中m<=n,进一步假设构成P和T的元素都是来自一个有限字母集\Sigma的字符。例如:\Sigma={0,1}或者\Sigma={a,b,...,z}。字符数组通常称为字符串。
我们用\Sigma^*表示所有有限长度字符串的集合,该字符串由字母表\Sigma中的字符组成。特别地,长度为0的空字符用\varepsilon表示,也属于\Sigma^*。一个字符串x的长度用|x|表示。两个字符串x和y的连结用xy来表示,长度为|x|+|y|,由x的字符串后接y的字符串构成。
如果0<=s<=n-m,并且T[s+1...s+m]=P[1...m](即如果T[s+j]=P[j],其中1<=j<=m),那么称模式P在文本T中出现,且偏移为s。如果P在T中以偏移s存在,那么称s是有效偏移;否则,称它为无效偏移。如图一,s=3就是一个有效位移。根据此约定,字符串匹配问题就可以变成:对于模式串P找出所有文本串T的有效偏移。
如果对于某个字符串y\in\Sigma^*有x=wy,则称字符串w是字符串x的前缀,记作w\sqsubset x。类似的,我们也可以定义后缀符号:若x=yw,则称字符串w是字符串x的后缀,记作w\sqsupset x。可以看出:如果w\sqsubset x,则|w|<=|x|。特别地,空字符串\varepsilon同时是任何一个字符串的前缀和后缀。
(想一想我们为什么要引入\sqsupset和\sqsubset符号。)
如果不做特殊说明,我们约定认为a为一个字符,即长度为1的字符串。
为了使符号简洁,我们把模式P的由前k个字符组成的前缀P[1...k]记作P_k,P_m=P,采用这种记号,我们又能够把字符串匹配问题表述成:
找到所有偏移s(0<=s<=n-m),使得P\sqsupset T_{s+m}。
首先,我们考虑朴素算法的操作过程
图一展示了一个针对文本串T模式串P的的一个特定位移s。它已经匹配到了P_q,在q+1的位置与文本串T失配。
按照朴素算法的操作,我们这时应进行s'=s+1,q=1的操作,把文本串的匹配指针左移到s'+1位,模式串P匹配指针移回1位,从头开始匹配。可这样时间开销是个很大的问题。
那怎么办呢?
我们能不能不把文本串的指针向左移,而直接把模式串的匹配指针对准下一个可能的匹配位置上,即只移动模式串P呢?
答案是可以的。
别忘了我们已经匹配好了P_q,这意味着我们已经知道了T[s+1...s+q]=P[1...q],如果能把这东西给利用起来那该多好啊!
怎么用呢?
于是,KMP算法就来了。
KMP主体
还是用图二。
KMP算法思想便是利用已经匹配上的字符信息,使得模式串的指针回退的字符位置能将主串与模式串已经匹配上的字符结构**重新对齐**。
什么意思?
假设我们存在这样一个映射函数,先把它理解成一个小黑盒。当我们在模式串$q+1$的位置上失配时,它能跳到$P$串的某一位置$k$(注意是$P$串),即$k=next[q]$使得$P_{k}$与先前已匹配的$q$个字符的文本串不发生冲突,然后再比较$k+1$的位置是否与当前文本串指针匹配,如果不能,那继续找$next[k]$;如果能,那就成功匹配一位,进行下一位的匹配。这样,**文本串的指针只会向右移而不会向左移**。那么这个匹配程序就很好实现了。
这里直接给出伪代码:
```cpp
KMP-MATCHER(T,P)
n = T.length
m = P.length
next = COMPUTE-PREFIX-FUNCTION(P)//这里的next就是那个小黑盒
q = 0
for i=1 to n
while q>0 and P[q+1]!=T[i]
q = next[q]
if P[q+1] == T[i]
q = q+1
if q == m
print "Pattern occurs with shift" i-m
q = next[q]//匹配成功后肯定要往回走啊
```
这就是$KMP$算法的主体!
(仔细回味下)
那我们怎么求这个$next[q]$呢?
我们来观察它的性质。
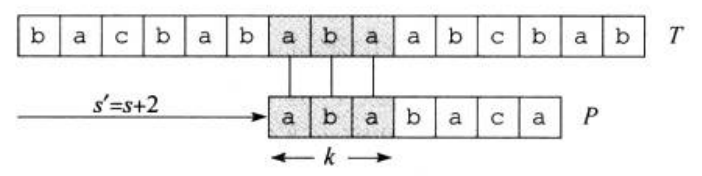
如图三,根据$q=5$个字符已经完全匹配,那么图中的$P_k\sqsupset T[s+1...s+q]$,且$k$是满足此条件的最大值,我们直接可以从$P[k+1]$开始与文本串匹配。也就是说,这里的$k$就是我们要找的$next[q]$。
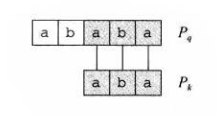
在图四中,我们把$P_q$和$P_k$单独拿了出来,你发现了什么?
$P_k\sqsupset P_q$!
可以看出$k$是满足条件的最大值,也就是说:
$next[q]=max$ { $k:k<q$且$P_k$ $\sqsupset$ $P_q$ }
为什么会是这样呢?
我们想要直接在$k+1$位开始匹配,就得保证$P_k\sqsupset T[s+1...s+q]$,虽然我们在$q+1$位失配,但我们已经知道了$P_q = T[s+1...s+q]$,所以即有$P_k\sqsupset P_q$。
那为什么我们会要求$k$为满足条件的最大值呢?
这里先简单理解,**$k$为最大值也就包含了$k$为更小值的情况**。
那么,这个$next$我们就把它视为$P$的**前缀函数**。
那么,怎么来求这个$next$呢?
首先,我们肯定能想到一种朴素算法,这里就不细说了,因为用朴素算法还不如敲个$O((n-m+1)m)$的匹配算法呢。。。
那我们怎么来优化求法呢?
同样假设,对于一个模式串$P$,我们已经知道了$next[1...q-1]$,现在,我们来计算$next[q]$。其中,$next[q-1]=k$。
## 引理1:当$P[k+1]=P[q]$时,可得$next[q]=k+1$。(前缀函数延续性引理)
证明:
因为:$next[q-1]=k$ 即 $P_k\sqsupset P_{q-1}$。
若字符$P[k+1]=P[q]$,则$P_{k+1}\sqsupset P_q$。
所以:$next[q]=k+1$。
证毕。
## 引理2:若$next[q-1]$的最大候选项为$k$,即$next[q-1]=k$,则它的次大候选项为$next[k]$,次次大为$next[next[k]]$......(前缀函数迭代引理)
证明:(反证法)
若存在$k_0$使得$P_{k_0}\sqsupset P_{q-1}$且$next[k]<k_0<k$。
因为:$next[q-1]=k$,即$P_k\sqsupset P_{q-1}$。
又因为:$k_0<k$。
所以:$P_{k_0}\sqsupset P_k$。
即:$next[k]=k_0$。
这与$next[k]<k_0$矛盾。
所以假设不成立。
证毕。
后面的依次类推。
由前两个引理可以看出,$next[q]$可能的候选项为:$next[q-1]+1$,$next[next[q-1]]+1$......而易知,$next[1]=0$。
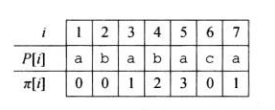
于是,我们便可以高效计算$next$数组。
```cpp
COMPUTE-PREFIX-FUNCTION(P)
m = P.length
pi[1] = 0
k = 0
for q=2 to m
while k>0 and P[k+1]!=P[q]
k = pi[k]
if P[k+1] == P[q]
k = k+1
pi[q] = k
```
是不是和$KMP-MATCHER$很像?
其实,实质上,**KMP算法求前缀函数的过程就是模式串的自我匹配**。
为什么我们先说$KMP$算法的主体再谈$next$的计算?其实这是从两种角度出发认识$KMP$。讲解主体的时候我们采用了假设法,这是一种十分感性的认知,比较好懂。在讲解$next$的计算时,我们引用了一些数学思维来帮助我们更加理解$KMP$。大家可以看出,实质上,$KMP$主体和$next$的计算是几乎一样的逻辑。
#### 至此,$KMP$算法原理的讲解到此结束。
-----------
## 参考文献
- 算法导论
- 算法进阶指南
- [详解KMP](https://www.cnblogs.com/yjiyjige/p/3263858.html)
- [剖析KMP](https://blog.csdn.net/v_july_v/article/details/7041827)
- [字符串匹配算法集合](https://blog.csdn.net/force_eagle/article/details/10340729)
------------
##### 附:以上文字均来自[Silent_EAG —— ~~一个可爱的女孩纸~~](https://www.luogu.org/space/show?uid=111674) [她的博客](http://www.cnblogs.com/silentEAG/)
------------
## 关于 kmp 算法中 next 数组的周期性质
### 引理:
对于某一字符串 $S[1$~$i ]$,在它众多的$ next[ i ] $的“候选项”中,如果存在某一个$ next[ i ] $,使得: $i$ % $( i - next[ i ] ) == 0$ ,那么 $S[ 1$~ $( i -next[ i ] ) ]$ 可以为 $S[ 1$ ~ $i ]$ 的循环元而 $i / ( i - next[ i ] )$ 即是它的循环次数 $K$。
### 证明如下:

如图,$next[ i ] = j$,由定义得红色部分两个子串完全相同。
那么有$S[ 1$~$j ] = S[ m$~$i ]$ $( m = i - next[ i ] )$。
------------

如果我们在两个子串的前面框选一个长度为 m 的小子串(橙色部分)。
可以得到:$S[ 1$~$m ] = S[ m$~$b ]$。
------------
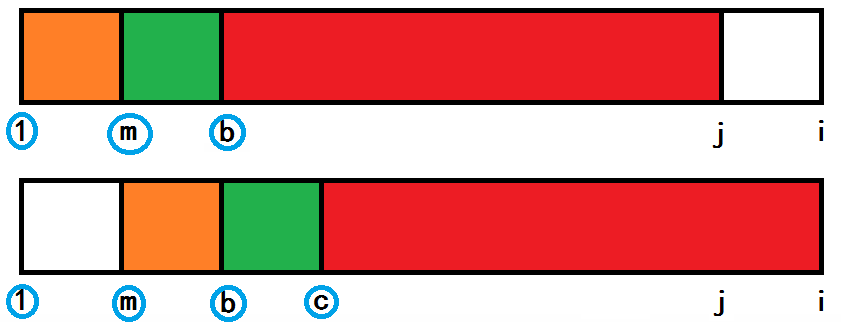
如果在紧挨着之前框选的子串后面再框选一个长度为 m 的小子串(绿色部分),同样的道理,
可以得到:$S[ m$~$b ] = S[ b$~$c ]
又因为:S[ 1~m ] = S[ m~b ]
所以:S[ 1~m ] = S[ m~b ] = S[ b~c ]
如果一直这样框选下去,无限推进,总会有一个尽头。
当满足 i % m == 0 时,刚好可以分出 K 个这样的小子串,
且形成循环( K = i / m )。
因此我们需要从 1~N 扫一遍,判断如果 next[ i ]
可以整除 i ,即满足 i % ( i - next[ ] ) == 0 ,那么就可以
肯定S[ 1~ ( i - next[ i ] ) ]是 S[ 1~i ] 的最小循环元,而
出这些 $i$和 $K$ 即可。
-------------
那么为什么只判断 $next[ i ]$ 而不判断 $next[?]$呢?
(注:$next[i]$和$next[?]$表述的意义不同,为方便描
述,这里定义$next[?]$为$next[i]$的$“候选项”中的某一个)
### 实际上由这道题可以总结出很多结论:
#### 结论一:
若$i-next[i]$可整除$i$,则$s[1$~$i]$具有长度为$i-next[i]
的循环元,即$s[1$~$i-next[i]]$。(前面的~~一大堆~~文
字和图片已经给出了这个结论的证明,同时结论一
也是后面推导其他结论的理论基础)
结论二:
若i-next[?]可整除i,则s[1~i]具有长度为i-next[?]
的循环元,即s[1~i-next[?]]。
(用与结论一同样的证明方法可以推导出结论二)
(由此处可知,i-next[?]想用作循环元要满足的
条件是:i-next[?]可整除i)。
结论三:
任意一个循环元的长度必定是最小循环元长度的倍数
结论四:
如果i-next[i]不可整除i,s[1~i-next[?]]一定
不能作为s[1~i]的循环元。
关于结论四的证明和扩展:
①.如果s[1~i-next[i]]不能作为s[1~i]循环元,那么
(即结论四)
②.如果$i-next[i]$不可整除$i$,$s[1$~$i]$一定不存在循环元。
③.如果$i-next[i]$不可整除$i$,$i-next[?]$也都一定不可整除$i$。
④.如果$s[1$~$m]$是$s[1$~$i]$的循环元,$next[i]$一定为$i-m$($i-m$一定为
$next[i]$)。(在算法竞赛进阶指南上有这么一句话:如果$s[1$~$m]$为$s[1$~$i]$的循
环元,$i-m$一定是$next[i]$的“候选项”,与此处意义略有不同)
⑤.若$m=i-next[i]$,$j=next[?]$,$next[j]=j-m$。(无论$m$可否整除$i$)
(由④扩展而来)
------------
#### 一些题外话:
关于③的证明,有一个很有趣的想法。
有两个数$a$,$c$和一个数的集合$b$,且$b$与$a$有一定的关系(限制)。
已知$a$不可整除$c$,证明$x(x∈b$)不可整除$c$(~~目前尚未成功~~)。
虽然表面上看起来并没有什么用,但这种思想把图形匹配转
化为了代数证明。
如果有大佬感兴趣可以思考一下。。。
###### 附:来自某**李姓**Math大佬。
------------
#### ②③④比较好理解,这个⑤是个什么意思呢?
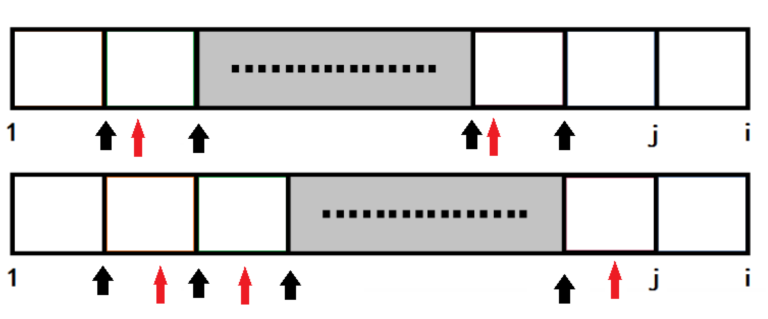
其实不难懂,通俗点说就是$i-next[?]$一定是在$m$的倍数处
$(m,2m,3m...)$,如果有循环,也可以说是$i-next[?]$一定在循环
节点上,或者说是一定在我们先前图片中框选的黑色块的边界相
邻处,不可能在某个黑色块的中间(如图红色为不可能的情况)
注意一下这个等式:$i-next[j]=i-j+m
可以化简为:next[j]=j-m
那么可以发现每个next[?]和next[next[?]]之间刚好相差m,
只是要由⑤推导①的话,用化简前的样子似乎会更好懂一些。
假如④⑤得证,那么它们和①有什么关系呢?
如果i-next[?]一定是在m的倍数处(m=i-next[i]),
因为当m不可整除i时,m的倍数也不可整除i,
所以i-next[?]均不满足作为s[1~i]循环元的条件(前面已
提到过“条件”具体指什么)。
因此,⑤→①得证。
如何证明④或者⑤?
如图,j=next[i],m=i-next[i]
先按照与之前相同的方法先将s[1~i]划分成K个黑色块
------------
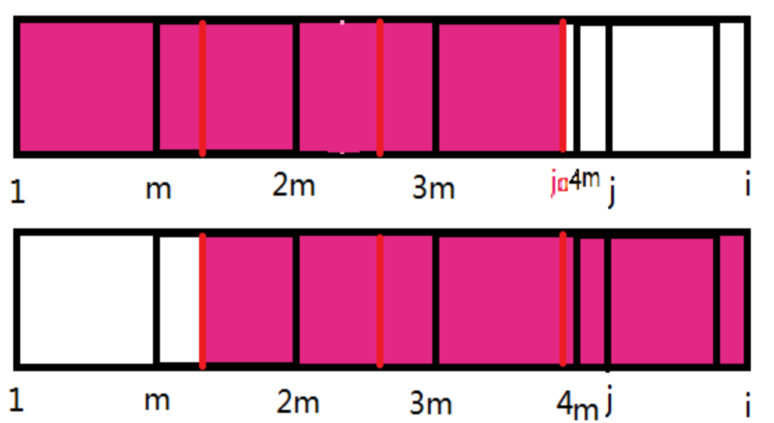
同样的,框选出红色块。
------------
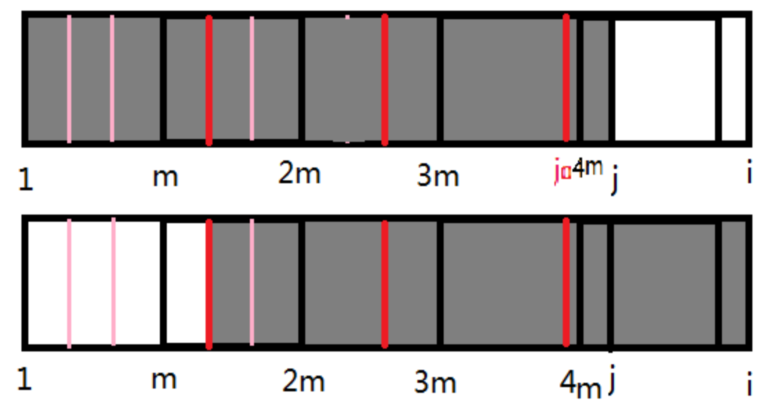
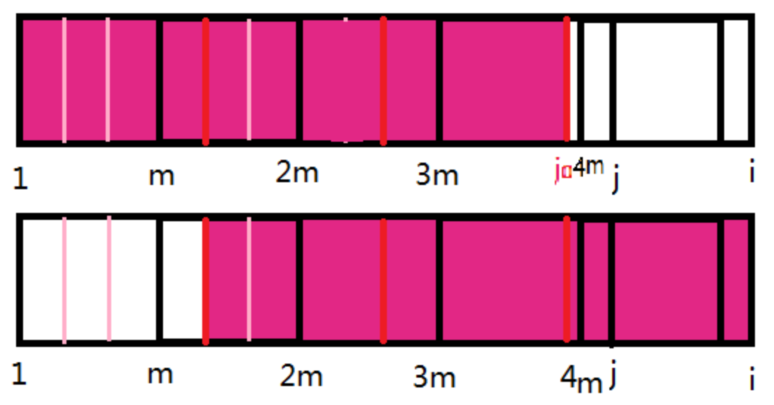
然后再作一些辅助线。接下来就开始推理。
设$v=j-j0$。
先看左边:$s[1$~$1+v]=s[m$~$m+v]$,$s[1+v$~$1+2v]=s[m+v$~$m+2v]
再看右边: s[1~1+v]=s[m+v~m+2v]
综合可得:s[1~1+v]=s[m~m+v]=s[m+v~m+2v]=s[1+v~1+2v]
无限的推进,再推进,辅助线划分出的长度为v的区域全部相等,直至边界。而此时的边界出现了两种情况:
⑴v可整除i。
此时刚好将s[1~i]分成了若干个完全相同的长度为v的小块,明显形成了循环元s[1~v],那么next[i]至少应为i-v,这与之前的next[i]=j相矛盾。
⑵v不可整除i。
观察下列图片,你发现了什么?
将蓝圈处放大,发现了一种交叉相等的情况(如图绿色处)。
再把它压扁,并取几个新的名字1',m',j',i'。此时它变得和初始
的情况一模一样,于是经过相同的操作后,再一次使出了无限
推进,假如每次的v'都不可整除m',那么就一路推了边界:v'=1。
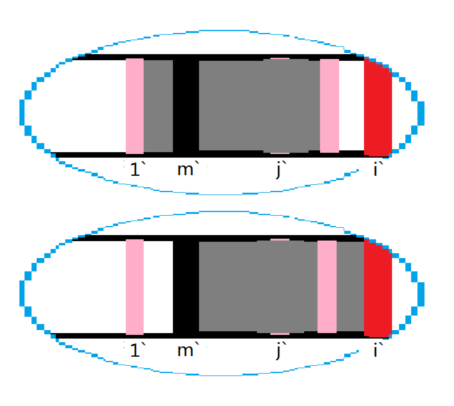
当n不在m的倍数处时,一定会出现矛盾,所以假设不成立。
因此④得证。同理⑤也得证。
----------
# 完结附代码:
```cpp
#include<cstdio>
int t,i,j,n,nex[1000005];char a[1000005];
int main(){
while(scanf("%d",&n),n){
scanf("%s",a+1);
printf("Test case #%d\n",++t);
for(i=2,j=0;i<=n;i++){//最基本的 next[] 数组求法
while(j&&a[i]!=a[j+1])j=nex[j];
if(a[i]==a[j+1])j++;nex[i]=j;
}
for(i=2;i<=n;i++)//由于1~1只有一个字母,只能是它本身构成长度为1的循环,所以从2开始枚举
if(i%(i-nex[i])==0&&nex[i])//判断时还要注意nex[i]是否为0
printf("%d %d\n",i,i/(i-nex[i]));
//如果i含有长度大于1的最小循环元,输出i的长度(即i)以及最大循环次数K(即i-nex[i])
printf("\n");//记得输出一个空行
}
}
```
~~写了这么多证明,结果最后代码简单得不要不要的。。。。。~~