P9173 题解
_buzhidao_
·
·
题解
题面传送门
题目分析
其实贪心不会超时,就是不能通过,详见这里。
这道题可以根据 a,b 的填写顺序,列成一张表。图可能有点丑。
显然,我们要从左上角移动到右下角,把 a,b 全部填写完。
我们只能向下或向右走。如果把所有路径都尝试一遍,就成了递归,必然超时。
所以我们需要——
动态规划
$dp_{i,j,0}$ 表示 $a$ 数组填写 $i$ 个数,$b$ 数组填写 $j$ 个数,$a$ 数组**当前的**最大值。
$dp_{i,j,1}$ 表示 $a$ 数组填写 $i$ 个数,$b$ 数组填写 $j$ 个数,$b$ 数组**当前的**最大值。
例如:
$a=(0),b=(0,0,1)$,已知 $dp_{0,3}=(0,5),dp_{1,2}=(6,4)$。目标:填充全部。可结合表格分析。
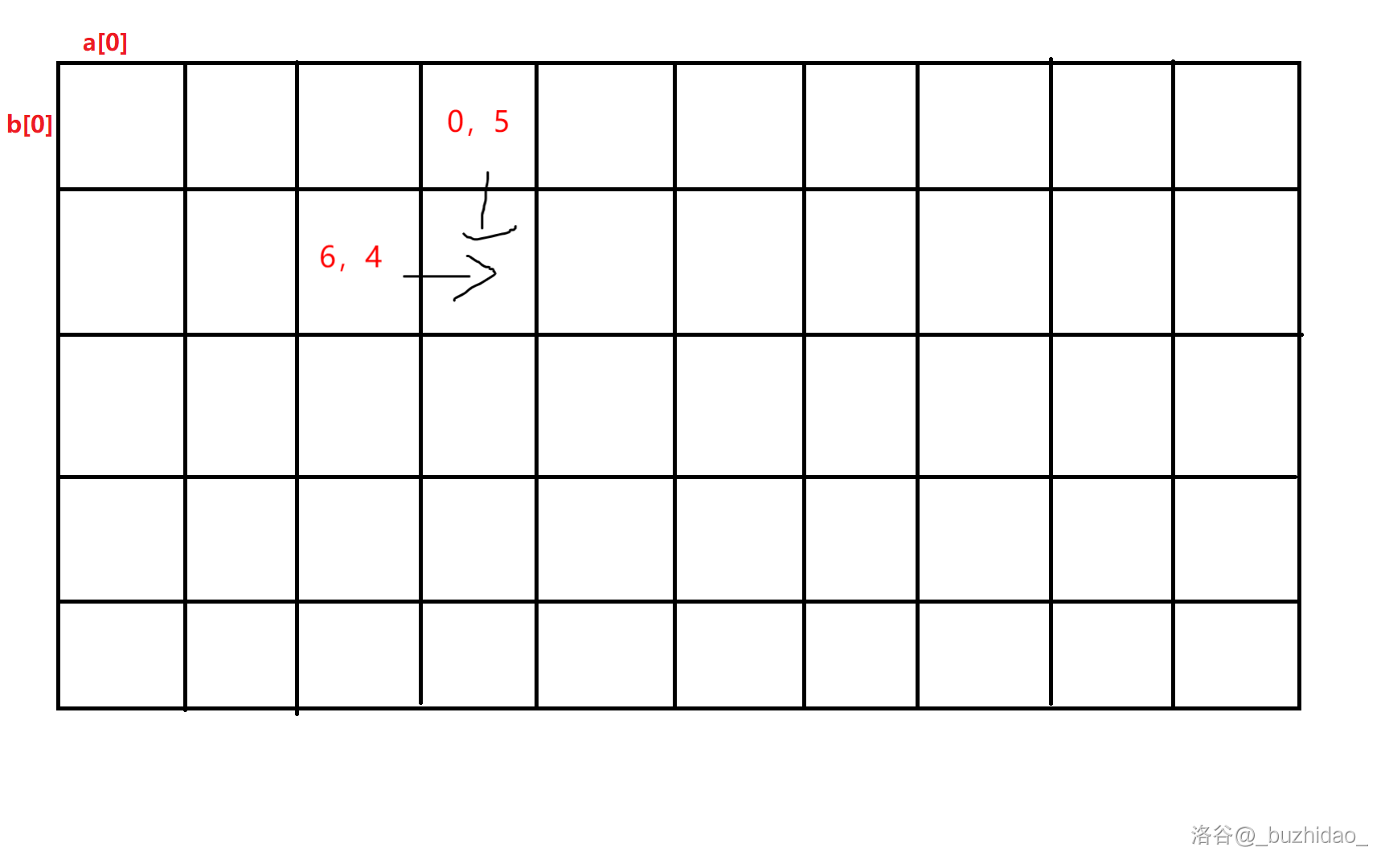
- 路径 $1$:从 $dp_{0,3}$ 开始填写:因为 $a_1 \ne b_3$,所以 $dp_{1,3}=(1,5)$。
- 路径 $2$:从 $dp_{1,2}$ 开始填写:因为 $b_3 \ne b_2$,所以 $dp_{1,3}=(6,5)$。
综上,因为要取**最小值**,所以得到答案 $=\min(\max(1,5),\max(6,5))=\min(5,6)=5$。
## 递推公式
$dp_{i,j}$ 初始化为 $(\inf,\inf)$。
#### 当 $i \ne 0$:
- 当 $a_i=a_{i-1}$:$dp_{i,j,0}=\min(dp_{i,j,0},dp_{i-1,j,0}+2)$,否则 $dp_{i,j,0}=\min(dp_{i,j,0},dp_{i-1,j,0}+1)$。
- 当 $a_i=b_j$:$dp_{i,j,0}=\min(dp_{i,j,0},dp_{i-1,j,1}+2)$,否则 $dp_{i,j,0}=\min(dp_{i,j,0},dp_{i-1,j,1}+1)$。
#### 当 $j \ne 0$:
- 当 $b_j=b_{j-1}$:$dp_{i,j,1}=\min(dp_{i,j,1},dp_{i,j-1,1}+2)$,否则 $dp_{i,j,1}=\min(dp_{i,j,1},dp_{i,j-1,1}+1)$。
- 当 $b_j=a_i$:$dp_{i,j,1}=\min(dp_{i,j,1},dp_{i,j-1,0}+2)$,否则 $dp_{i,j,1}=\min(dp_{i,j,1},dp_{i,j-1,0}+1)$。
# AC代码
```cpp
#include<bits/stdc++.h>
using namespace std;
int dp[5005][5005][2];
int n,m,a[5005],b[5005];
const int inf=1e9;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);//IO优化
cin>>n;for(int i=1;i<=n;++i) cin>>a[i];
cin>>m;for(int i=1;i<=m;++i) cin>>b[i];
for(int i=0;i<=n;++i){
for(int j=0;j<=m;++j){
if(i==0&&j==0) continue;//这种情况不存在
dp[i][j][0]=inf;
//为防止代码过长,加以适当简化
if(i){
dp[i][j][0]=min(dp[i][j][0],dp[i-1][j][0]+1+(bool)(a[i]==a[i-1]));
dp[i][j][0]=min(dp[i][j][0],dp[i-1][j][1]+1+(bool)(a[i]==b[j]));
}
dp[i][j][1]=inf;
if(j){
dp[i][j][1]=min(dp[i][j][1],dp[i][j-1][1]+1+(bool)(b[j]==b[j-1]));
dp[i][j][1]=min(dp[i][j][1],dp[i][j-1][0]+1+(bool)(b[j]==a[i]));
}
}
}
cout<<min(dp[n][m][0],dp[n][m][1]);//输出最优方案
return 0;
}
```