x \times dis + B \times (l_1+l_2) > y \times dis + A \times l_1 + B \times l_2z \times dis + A \times (l_1+l_2) > y \times dis + A \times l_1 + B \times l_2
整理得:
$(z-y) \times dis > (B-A) \times l_2$。
也就是 $\frac{y-x}{l_1} < \frac{B-A}{dis} < \frac{z-y}{l_2}$。
也就是保留的行和列满足其位置与代价作为点坐标映射到平面上后,构成一个下凸壳。
到这里性质就看上去很强了,考虑做原问题。
依然考虑每次转移一个 L 行路径,我们观察满足什么性质的转移才是有用的以减少转移数。
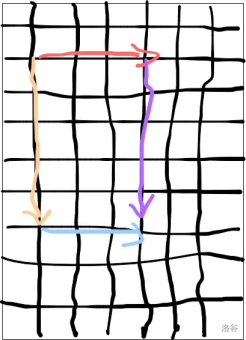
设红色路径代价为 $x$,蓝色路径代价为 $y$,橙色路径代价为 $z$,紫色路径代价为 $w$,这四条路径分别对应点 $P_1,P_2,P_3,P_4$,横向移动距离为 $l_1$,纵向移动距离为 $l_2$。
如果向下拐更优的话,那么应当有:$z \times l_2 + y \times l_1 < x \times l_1 + w \times l_2$。
整理得到 $\frac{y-x}{l_2} < \frac{w-z}{l_1}$。
也就是从 $k_{P_1,P_2} < k_{P_3,P_4}$。
这表明我们将整个过程视作在保留的行和列上按顺序依次向后跳跃,那么跳跃的两点的斜率不减。
然而还是没有办法转移,因为一个极小 dp 过程太大,转移还是太复杂。
考虑再次拆分 L 形路径,注意到保留的行和列在某个时刻总会被经过,我们直接拆成若干个单独的点,也就是在保留的行和列上按顺序(这里不需要依次)向后**一个一个地**跳,继续观察性质,考察这个时候经过的行和列按顺序写下来是什么。
不难发现是将列构成的序列按顺序插入行构成的序列,不妨以 $N$ 代表行点,$M$ 代表列点,考虑将之前的 L 形路径的结论套过来,观察形如 $N_1,M_1,M_2,N_2,N_3,N_4,M_3,M_4$ 的点对,如果 $k_{N_1,N_2} > k_{M_2,M_3}$,那么这个序列就不如 $N_1,M_1,M_2,M_3,N_2,N_3,N_4,M_4$。
所以当你决定下一个放 $N$ 还是 $M$ 时,你一定会放扩展过去斜率更小的,不然你就可以按照上面的方法进行调整,如果两个选择斜率一样,不难发现无论放哪个,其代价与对后面的影响都一样。那么我们维护两个指针将保留的行与列扫一遍即可。
时间复杂度 $O(n+m)$。
```cpp
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e5+114;
int n,m,a[maxn],b[maxn];
pair<int,int> stk[maxn][2];
int ans,now[2],tp[2];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
while(tp[0]>=2&&(a[i]-stk[tp[0]][0].second)*(stk[tp[0]][0].first-stk[tp[0]-1][0].first)<(stk[tp[0]][0].second-stk[tp[0]-1][0].second)*(i-stk[tp[0]][0].first)){
tp[0]--;
}
stk[++tp[0]][0]=make_pair(i,a[i]);
}
for(int i=1;i<=m;i++){
cin>>b[i];
while(tp[1]>=2&&(b[i]-stk[tp[1]][1].second)*(stk[tp[1]][1].first-stk[tp[1]-1][1].first)<(stk[tp[1]][1].second-stk[tp[1]-1][1].second)*(i-stk[tp[1]][1].first)){
tp[1]--;
}
stk[++tp[1]][1]=make_pair(i,b[i]);
}
now[0]=now[1]=1;
int x=stk[now[1]][1].second,y=stk[now[0]][0].second;//两维移动代价
for(int i=1;i<=tp[0]+tp[1]-2;i++){
if(now[0]==tp[0]){
ans+=(stk[now[1]+1][1].first-stk[now[1]][1].first)*y;
now[1]++;
x=stk[now[1]][1].second;
}else if(now[1]==tp[1]){
ans+=(stk[now[0]+1][0].first-stk[now[0]][0].first)*x;
now[0]++;
y=stk[now[0]][0].second;
}else if((stk[now[0]+1][0].second-stk[now[0]][0].second)*(stk[now[1]+1][1].first-stk[now[1]][1].first)<(stk[now[1]+1][1].second-stk[now[1]][1].second)*(stk[now[0]+1][0].first-stk[now[0]][0].first)){
ans+=(stk[now[0]+1][0].first-stk[now[0]][0].first)*x;
now[0]++;
y=stk[now[0]][0].second;
}else{
ans+=(stk[now[1]+1][1].first-stk[now[1]][1].first)*y;
now[1]++;
x=stk[now[1]][1].second;
}
}
cout<<ans<<"\n";
return 0;
}
```