AT_joisc2019_e ふたつの料理 (Two Dishes)
紊莫
·
·
题解
这个题并不难,在此写一篇比较易懂的题解。
约定
$s_i$ 表示 $\text{A}$ 中第 $i$ 个任务的限定时间,$p_i$ 表示其代价。
$t_i$ 表示 $\text{B}$ 中第 $i$ 个任务的限定时间,$q_i$ 表示其代价。
---
首先 $\mathcal{O}(n^2)$ 的 DP:
设 $f(i, j)$ 表示 $\text{A}$ 序列中选取了 $[1, i]$,$\text{B}$ 序列中选取了 $[1, j]$ 的最优代价。
转移考虑 $f(i, j) \to f(i + 1, j)$ 和 $f(i, j) \to f(i, j + 1)$,因为 $i, j$ 确定了,当前的时间也是确定的,转移是简单的。
首先考虑把题目中所给的关于时间的限制转化一下:
对于 $A_i$ 这个任务,要求完成时间 $\le s_i$,注意到一个事实,我们在完成了 $A_i$ 的时候,一定完成了 $A_{1\dots i - 1}$ 中所有的任务。
那么我们在 $B$ 序列中至多能做的任务是一个前缀。
同理,对 $B$ 序列的也有类似的定义,形如做完了 $B_i$,且完成时间在 $t_i$ 内(也就是可以得到权值),那么此时 $A$ 中最多做 $x$ 个任务。
我们把两者的形式统一,为此,我们先假设所有 $p_i$ 都能被顺利得到,尽管这不一定,然后再把得不到的从答案中减去。
对于 $B_i$ 的形式为,当我们**将要**选择 $A_x$ 时,若此时 $B_i$ 已经被完成了,那么答案加上 $q_i$。
对于 $A_i$ 的形式为,当我们**将要**选择 $A_i$ 时,若此时 $B_x$ 已经被完成了,那么答案减去 $p_i$。
这些操作都可以挂在对应的 $x$ 上。
然后我们还是维护 $f(i, j)$ 这个 DP。
我们对 $i$ 这一维扫描线,动态的维护当前的 $f(j)$。
每一次操作中若此时 $B_x$ 已经被完成了,相当于是对一段后缀加上一个权值,然后做一次前缀 $\max$。
前缀 $\max$ 是怎么来的呢?
考虑另一种刻画问题的方法,我们将其看作是一个格路模型,$f(i, j)$ 就是到 $(i, j)$ 这个点的最大权值。
我们把权值都附在格子中(区别于 $(i, j)$ 这样的格点),那么 $f(i, j) \to f(i + 1, j)$ 就是加上线段 $(i, j) \to (i + 1, j)$ 下方格子的权值。
向上不会增加任何权值,但是 $f(i, j) \to f(i, j + 1)$,在 DP 数组上体现为前缀 $\max$。
最后我们实现这个后缀加,前缀 $\max$ 即可,我们采用差分的方法,记录 DP 数组的差分数组为 $c$,那么对于 $[x, m]$ 的后缀加可以看作是 $c_x$ 的单点加。
如何求解前缀 $\max$ 呢?
分类讨论一下,如果加上的是一个正整数,那么前缀 $\max$ 显然是不变的,只需要在 $c_x$ 修改一下即可。
如果是一个负数,那么可能会出现如下的情况(黑实线表示真实的 DP 值)。
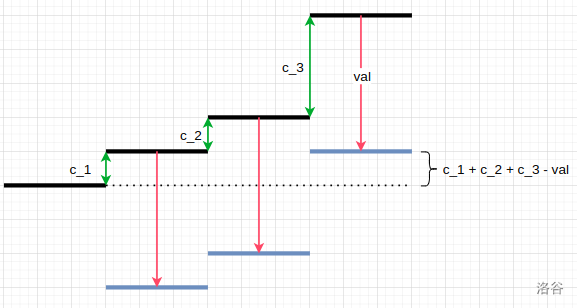
那么发现我们只需要找到第一处差分数组之和大于等于下降高度 $val$ 的地方,修改其值即可。
最后一个小问题,我们需要对 $f(j)$ 先加后减,因为我们每次都会取前缀 $\max$,如果先操作负数,可能会出现一个值很小了,但是被前缀 $\max$ 变大,然后再做加法就会偏大。
差分数组只用记录非 $0$ 的位置,每次删除的复杂度均摊是对的,总复杂度线性对数。