反射容斥
NahX_
·
·
算法·理论
同步至 博客园。
这篇文章中有讲基础的卡特兰数。
因为 OI 中的习惯,本文用 (n,m) 表示平面直角坐标系上 x=m,y=n 的点。
单线限制
根据卡特兰数,考虑拓展。
· 每次向上或向右,从 (0,0) 走到 (n,m) 不越过 A:y=x+k 的方案数。
将向上走视作 +1,向右走为 -1。自由路径数就是,由 n 个 +1,m 个 -1 组成的序列数为 {n+m\choose n}。
同样的,将除去第一个越过 A 的前缀后剩下的序列反转。该前缀一定是由 x+k+1 个 +1 与 x 个 -1 构成,则反转后整个序列变为由 m+k+1 个 +1,n-k-1 个 -1 组成的序列,有 {n+m\choose n-k-1}。类似卡特兰数中的方法容易证明这是一个双射。则原问题的答案为 {n+m\choose n}-{n+m\choose n-k-1}。
相当于从 (0,0) 到 (m+k+1,n-k-1) 的自由路径数。
也就是说,对于不越过 y=x+k 的情况,不合法方案数相当于作 (n,m) 关于直线 y=x+k+1/y=x+k-1 对称得到 (n',m') 后,(0,0) 到 (n',m') 的路径数。
所以下文都将不能越过 y=x+k 转化为不能触碰 y=x+k+1/y=x+k-1。
双线限制
· 每次向上或向右,从 (0,0) 走到 (n,m) 不触碰 A:y=x+k,B:y=x+k' 的方案数。
首先两条线如果 k 均 >0/<0 显然等价于单线限制,所以只考虑两线在 (0,0) 两侧的情况。
依旧考虑自由路径数减去不合法的路径数。不合法的路径数等价 c_0+c_1,c_0 为第一次非法触碰 A 的路径数,c_1 为第一次非法触碰 B 的路径数。
定义一条非法路径的表示为形如 ABABA\cdots 表示该路径依次触碰了 A,B 线(中间若连续经过多次相同的 A/B 看作一次)。c(S) 表示路径 S 的数量。
问题在于怎么求出这两个路径数。
如何求出越过 A 的路径数在上文已经解决了,也就是能求出任意 c(...A...)。同理能求出任意 c(...B...)。
要求出 c_0 等价于容斥 c(...A...)-c(...BA...)+c(...ABA...)\cdots。c_1 同理。
假设其中一条路径形如:
这时候将 B 关于 A 对称得到 B'。
此时若反转后得到的路径(即红色部分)触碰了 B',就相当于 ...AB... 的路径。(显然触碰 B' 时必定先触碰了 A。中间可能又经过了若干次 A,不过没有影响,这也是为什么要把连续经过相同的看作一次)。
又转为单线限制,即 (0,0) 到 (n',m') 且触碰了 B'。由上文,即为 (0,0) 到 (n'',m'') 的自由路径数等价于 c(...AB...)。
通透了。定义 R_l(x) 表示点/直线 x 关于直线 l 对称后的结果。
先考虑 A 往上的部分。
对于 c(...S...),|S|\ge 2,S=ABABA\cdots。记 L_i 为 R_{L_{i-1}}(L_{i-2}),L_2=A,L_1=B。以及 P_i=R_{L_i}(P_{i-1}),P_1:(n,m)。形式化的:
$(0,0)$ 到 $P_i$ 的自由路径数等价于 $c(...S:[1,i]...)$。若 $P_i$ 不在第一象限中则意味着不存在这种情况。
$B$ 往下的部分同理。
到这里就能够容斥了。
但是实现上有一个很简单的写法。将 $A,B$ 两线固定,求 $c(...A...)$ 时将 $p$ 关于 $A$ 对称,再求 $c(...BA...)$ 时只需要将 $p'$ 关于 $B$ 对称,再关于 $A$ 对称求 $c(...ABA...)$,以此类推。这个是容易得出的。从 $A\to B$($B\to A$) 至少需要 $k_1-k$ 步,复杂度为 $O(\frac{n+m}{|k_1-k|})$。
## 应用
### [P3266 [JLOI2015] 骗我呢](https://www.luogu.com.cn/problem/P3266)
首先根据一行内的限制容易得出每行形如除了 $a$ 其他的数按升序出现。
考虑第二个限制。实际上是 $a_i$ 与 $a_{i-1}$ 的关系。
两行形如:
$$1,2,3,...,a_{i-1}-1,a_{i-1}+1,...,m$$
$$1,2,3,...,a_i-1,a_i+1,...,m$$
当 $a_{i-1}=a_{i}+2$ 开始就不合法了,形如。
$$1,2,3,...,a_i-1,a_i,a_i+1,a_i+3,...,m$$
$$1,2,3,...,a_i-1,a_i+1,...,m$$
设计状态 $f_{i,j}$ 表示第 $i$ 行 $j$ 未出现的方案数,根据限制容易得方程。
$f_{i,j}=\sum_{k\le j+1}f_{i-1,k}
发现这是一个前缀和的形式,写作 f_{i,j}=f_{i,j-1}+f_{i-1,j+1}。
最后的答案为 \sum_{i=0}^m f_{n,i}=f_{n+1,m}。
放在坐标系上观察:
简单转化一下:
::::info[code]
```cpp
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define fin(x) freopen(#x".in","r",stdin)
#define fout(x) freopen(#x".out","w",stdout)
#define fr(x) fin(x),fout(x);
#define Fr(x,y) fin(x),fout(y)
#define INPUT(_1,_2,FILE,...) FILE
#define IO(...) INPUT(__VA_ARGS__,Fr,fr)(__VA_ARGS__)
using namespace std;
using namespace __gnu_pbds;
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define cfast ios::sync_with_stdio(false);cin.tie(0),cout.tie(0)
#define ll long long
#define ull unsigned long long
#define intz(x,y) memset((x),(y),sizeof((x)))
char *p1,*p2,buf[100000];
#define nc() (p1==p2 && (p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
#define tup(x) array<int,(x)>
inline ll read(){
ll x=0,f=1;char ch=nc();
while(ch<48||ch>57){if(ch=='-')f=-1;ch=nc();}
while(ch>=48&&ch<=57)x=x*10+ch-48,ch=nc();
return x*f;
}
//void write(int x){cout<<x<<' ';}
//void write(pii x){cout<<"P("<<x.fi<<','<<x.se<<")\n";}
//void write(vector<auto>x){for(auto i:x)write(i);cout<<'\n';}
//void write(auto *a,int l,int r){for(int i=l;i<=r;i++)write(a[i]);cout<<'\n';}
inline ll lowbit(ll x){return x&-x;}
#define pcount(x) __builtin_popcount(x)
inline void cmx(auto &x,ll y){if(y>x)x=y;}
inline void cmn(auto &x,ll y){if(y<x)x=y;}
inline int max(vector<int>w){int res=-1e9;for(int i:w)cmx(res,i);return res;}
const int mod=1e9+7;
#define int ll
#define f(x,y) C((x)+(y),(y))
ll qp(ll x,int y){ll res=1;for(;y;x=x*x%mod,y>>=1)if(y&1)res=res*x%mod;return res;}
const int N=3e6+5;
int fac[N],ifac[N];
int C(int x,int y){return (x<y||x<0||y<0)?0:fac[x]*ifac[y]%mod*ifac[x-y]%mod;}
void chg(int &x,int &y,int k){swap(x,y),x-=k,y+=k;}
inline void UesugiErii(){
int n,m,ans,V;cin>>n>>m,V=(n<<1)+m+3;
for(int i=fac[0]=1;i<=V;i++)fac[i]=fac[i-1]*i%mod;
ifac[V]=qp(fac[V],mod-2);
for(int i=V;i;i--)ifac[i-1]=ifac[i]*i%mod;
ans=C(2*n+m,n);
for(int x=n+m,y=n;x>=0&&y>=0;)
chg(x,y,2),(ans+=mod-f(x,y))%=mod,
chg(x,y,-1-m),(ans+=f(x,y))%=mod;
for(int x=n+m,y=n;x>=0&&y>=0;)
chg(x,y,-1-m),(ans+=mod-f(x,y))%=mod,
chg(x,y,2),(ans+=f(x,y))%=mod;
cout<<ans;
}
signed main(){
//IO();//cfast;
int _=1;//cin>>_;
for(;_;_--)UesugiErii();
return 0;
}
```
::::
### [Math Exam](https://qoj.ac/problem/8147)
$$
4S_i=4S_{i-1}+4a_i=a_i^2+2a_i+1
$$
$$4S_{i-1}=(a_i-1)^2\to \sqrt{S_{i-1}}=\frac{|a_i-1|}{2}$$
$$\sqrt{S_i}=\frac{|a_i+1|}{2}$$
必须保证 $S_i$ 为整数,也就是要保证 $a_i$ 为奇数。然后分情况讨论 $a_i\le -1$ 与 $1\le a_i$,发现等价于 $\sqrt{S_i}=\sqrt{S_{i-1}}\pm 1$。
于是就转化为从 $(0,0)$ 出发,每次向右上或右下走一步,不能碰到 $y=-1$,$y=\frac{m+1}{2}$,走到任意 $(i,n)$ 的路径数。
考虑将整个坐标系逆时针旋转 $45^{\circ}$。
变为从 $(0,0)$ 出发,每步向上或向右走,不能碰到 $y=x-1$,$y=x+\frac{m+1}{2}$,走到 $y=x+n$ 上任意一点的路径数。枚举终点。
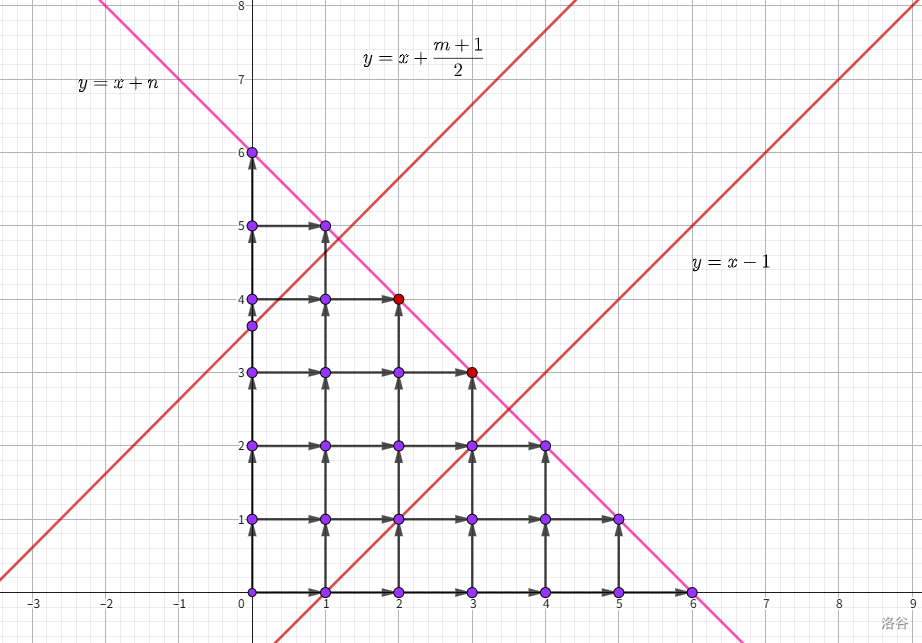
图中红色点即为能作为终点的位置。
复杂度 $O(m\frac{n+m}{m})=O(n+m)$。
其实这里不旋转也是可以的,起止点已知容易得出多少步向右上走,同样容易计数。
::::info[code]
```cpp
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define fin(x) freopen(#x".in","r",stdin)
#define fout(x) freopen(#x".out","w",stdout)
#define fr(x) fin(x),fout(x);
#define Fr(x,y) fin(x),fout(y)
#define INPUT(_1,_2,FILE,...) FILE
#define IO(...) INPUT(__VA_ARGS__,Fr,fr)(__VA_ARGS__)
using namespace std;
using namespace __gnu_pbds;
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define cfast ios::sync_with_stdio(false);cin.tie(0),cout.tie(0)
#define ll long long
#define ull unsigned long long
#define intz(x,y) memset((x),(y),sizeof((x)))
char *p1,*p2,buf[100000];
#define nc() (p1==p2 && (p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
#define tup(x) array<int,(x)>
inline ll read(){
ll x=0,f=1;char ch=nc();
while(ch<48||ch>57){if(ch=='-')f=-1;ch=nc();}
while(ch>=48&&ch<=57)x=x*10+ch-48,ch=nc();
return x*f;
}
//void write(int x){cout<<x<<' ';}
//void write(pii x){cout<<"P("<<x.fi<<','<<x.se<<")\n";}
//void write(vector<auto>x){for(auto i:x)write(i);cout<<'\n';}
//void write(auto *a,int l,int r){for(int i=l;i<=r;i++)write(a[i]);cout<<'\n';}
inline ll lowbit(ll x){return x&-x;}
#define pcount(x) __builtin_popcount(x)
inline void cmx(auto &x,ll y){if(y>x)x=y;}
inline void cmn(auto &x,ll y){if(y<x)x=y;}
inline int max(vector<int>w){int res=-1e9;for(int i:w)cmx(res,i);return res;}
const int mod=998244353;
//#define int ll
#define f(x,y) C((x)+(y),(y))
ll qp(ll x,int y){ll res=1;for(;y;x=x*x%mod,y>>=1)if(y&1)res=res*x%mod;return res;}
const int N=1e7+5;
int fac[N],ifac[N];
inline int C(int x,int y){return (x<y||x<0||y<0)?0:1ll*fac[x]*ifac[y]%mod*ifac[x-y]%mod;}
inline void chg(int &x,int &y,int k){swap(x,y),x-=k,y+=k;}
inline double get(int b,int b_){return (b_-b)*1.0/2;}
inline void UesugiErii(){
int n,m,V;ll ans=0;cin>>n>>m;
for(int i=fac[0]=1;i<=n;i++)fac[i]=1ll*fac[i-1]*i%mod;
ifac[n]=qp(fac[n],mod-2);
for(int i=n;i;i--)ifac[i-1]=1ll*ifac[i]*i%mod;
int s=floor(get((m+1)/2+1,n)),t=ceil(get(-1,n));
for(int X=max(s+1,0);X<t;X++){
int Y=-X+n;ans+=C(X+Y,X);
for(int x=X,y=Y;x>=0&&y>=0;)
chg(x,y,(m+1)/2+1),(ans+=mod-f(x,y))%=mod,
chg(x,y,-1),(ans+=f(x,y))%=mod;
for(int x=X,y=Y;x>=0&&y>=0;)
chg(x,y,-1),(ans+=mod-f(x,y))%=mod,
chg(x,y,(m+1)/2+1),(ans+=f(x,y))%=mod;
}
cout<<ans<<'\n';
}
signed main(){
//IO();
cfast;
int _=1;//cin>>_;
for(;_;_--)UesugiErii();
return 0;
}
```
::::
### [CF1967E1 Again Counting Arrays (Easy Version)](https://www.luogu.com.cn/problem/CF1967E1)
把 $b$ 看作是网格图中每步向右上或右下。首先考虑判定合法的条件。发现 $a$ 的限制很松,只有在 $a_{i+1}=b_i+1$ 时 $b_{i+1}$ 才会向右下走一步,直到存在 $b_i=0$ 且需要向右下走时不合法。并且只要 $b_i=m$ 那往后每次向上走即可相当于 $a$ 无限制。
设计状态 $f_{i,j}$ 表示第 $i$ 轮 $b_i=j$ 的方案数。
$$
f_{i,j}=\begin{cases}
f_{i-1,j-1}\cdot (m-1)\\
f_{i-1,j+1} & ,j<m\\
f_{i-1,m}\cdot m & ,j=m
\end{cases}
$$
复杂度 $O(nm)$。
发现这是一个类似格路计数状物,不能碰到 $y=-1$,$y=m$,起点 $(0,b_0)$,终点在 $(i,n),i\in[0,\min\{n+b_0,m-1\}]$。
但是碰到 $y=m$ 也是合法状态,需要额外计数,枚举碰到 $y=m$ 的位置 $(m,x)$ 相当于双线限制走到 $(m-1,x-1)$。
还有一个问题是向右上走需要乘上 $(m-1)$ 的权,所以不完全是自由路径数。但是已知起点 $(0,b_0)$ 终点 $(x,y)$,容易得到向上走了 $\frac{x+y-b_0}{2}$ 步。
所以得到容斥后的自由路径数乘上 $(m-1)^{\frac{x+y-b_0}{2}}$ 即可。
放进去,则每次路径数变为 $(m-1)^{\frac{x+y-b_0}{2}}{x\choose \frac{x+y-b_0}{2}}$。还有就是在碰到 $y=m$ 后,剩下的 $a$ 相当于无影响,任意填则需乘上 $m^{n-x}$。
复杂度 $O(\frac{n(n+m)}{m})=O(\frac{n^2}{m})$。
这两种做法的复杂度很显然是能够根号分治做到 $O(n\sqrt n)$。
### [CF1967E2 Again Counting Arrays (Hard Version)](https://www.luogu.com.cn/problem/CF1967E2)
考虑这个格路计数的本质。
不合法的情况实际上是 $A:y=-1$,$B:y=m$ 的双线限制中,第一次非法碰到 $B$ 的情况数 $C$。发现其实就相当于一开始的 $c_0$($c_1$)。
因为碰到 $A$ 或 $B$ 后剩下的 $a$ 已经没有影响了,也就是没有限制,等价于剩下的任意走。所以就将终点全部挪到第 $n$ 列上了。
所以只需枚举终点 $p:(i,n),i\in[b_0+n,b_0-n]$,计算 $C$。
考虑 $i\le -1$ 则必定会经过 $B$,否则需关于 $B$ 对称得到 $y_{p'}\le -1$ 所以考虑 $y_p\le -1$ 的情况即可。
按照上文计算 $c_0,c_1$ 的方法,将 $p$ 依次关于 $ABABAB\cdots$ 对称求方案数。
对称到 $(x,n)$ 贡献为 $(m-1)^{\frac{n+i-b_0}{2}}{n\choose \frac{n+x-b_0}{2}}$ 至于为什么前一项的指数是 $i$ 而不是 $x$,因为上文提到过第一项其实是在容斥得到固定终点的路径数后才乘的权值,分配律放进去不变。
每次对称后得到:
$p,2m-p,-2m-2-p,4m+2+p,-4m-4-p,\cdots
(第一项 p 为必定经过 B 的路径数)。
发现奇数项、偶数项分别为两个等差数列。并且对系数的贡献均相等为 (m-1)^{\frac{n+i-b_0}{2}}。
维护 {n\choose i} 的系数,分别以 2m+2,-2m-2 作差分,最后还原出每个 {n\choose i} 的系数计算即可。
::::info[code]
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define fin(x) freopen(#x".in","r",stdin)
#define fout(x) freopen(#x".out","w",stdout)
#define fr(x) fin(x),fout(x);
#define Fr(x,y) fin(x),fout(y)
#define INPUT(_1,_2,FILE,...) FILE
#define IO(...) INPUT(__VA_ARGS__,Fr,fr)(__VA_ARGS__)
using namespace std;
using namespace __gnu_pbds;
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define cfast ios::sync_with_stdio(false);cin.tie(0),cout.tie(0)
#define ll long long
#define ull unsigned long long
#define intz(x,y) memset((x),(y),sizeof((x)))
char *p1,*p2,buf[100000];
#define nc() (p1==p2 && (p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
#define tup(x) array<int,(x)>
inline ll read(){
ll x=0,f=1;char ch=nc();
while(ch<48||ch>57){if(ch=='-')f=-1;ch=nc();}
while(ch>=48&&ch<=57)x=x*10+ch-48,ch=nc();
return x*f;
}
//void write(int x){cout<<x<<' ';}
//void write(pii x){cout<<"P("<<x.fi<<','<<x.se<<")\n";}
//void write(vector<auto>x){for(auto i:x)write(i);cout<<'\n';}
//void write(auto *a,int l,int r){for(int i=l;i<=r;i++)write(a[i]);cout<<'\n';}
inline ll lowbit(ll x){return x&-x;}
#define pcount(x) __builtin_popcount(x)
#define f(x) (n+(x)-b)
inline void cmx(auto &x,ll y){if(y>x)x=y;}
inline void cmn(auto &x,ll y){if(y<x)x=y;}
inline int max(vector<int>w){int res=-1e9;for(int i:w)cmx(res,i);return res;}
const int mod=998244353;
inline ll qp(ll x,int y){ll res=1;for(;y;x=x*x%mod,y>>=1)if(y&1)res=res*x%mod;return res;}
const int N=4e6+5;
ll c0[N],c1[N],pw[N],fac[N],ifac[N],ans;int n,m,b,V;
inline int C(int x,int y){return x<y?0:1ll*fac[x]*ifac[y]%mod*ifac[x-y]%mod;}
inline void UesugiErii(){
cin>>n>>m>>b;
for(int i=0;i<=n*2;i++)c0[i]=c1[i]=0;
for(int i=pw[0]=1;i<=n;i++)pw[i]=pw[i-1]*(m-1)%mod;
for(int i=ans=1;i<=n;i++)ans=ans*m%mod;
if(n<=b||m<=b)return cout<<ans<<'\n',void();
for(int i=b-n,t;i<=-1;i++)if(!((i-b+n)&1)){
t=f(i),c0[t]=(c0[t]+pw[f(i)/2])%mod;
t=f(m*2-i);
if(t>=0&&t<=n*2)c1[t]=(c1[t]+mod-pw[f(i)/2])%mod;
}
for(int _i=0,i,t;_i<=b+n;_i++)if(!((_i-b+n)&1)&&(i=-_i-2)>=b-n){
t=f(i),c0[t]=(c0[t]+pw[f(_i)/2])%mod;
t=f(m*2-i);
if(t>=0&&t<=n*2)c1[t]=(c1[t]+mod-pw[f(_i)/2])%mod;
}
for(int i=n*2-m*2-2;i>=0;i--)
(c0[i]+=c0[i+m*2+2])%=mod;
for(int i=m*2+2;i<=n*2;i++)
(c1[i]+=c1[i-m*2-2])%=mod;
for(int i=0;i<=n*2;i+=2)
ans=(ans+mod-(c0[i]+c1[i])%mod*C(n,i/2)%mod)%mod;
cout<<ans<<'\n';
}
signed main(){
//IO();
cfast;
int V=4e6;
for(int i=fac[0]=1;i<=V;i++)fac[i]=fac[i-1]*i%mod;
ifac[V]=qp(fac[V],mod-2);
for(int i=V;i;i--)ifac[i-1]=ifac[i]*i%mod;
int _=1;cin>>_;
for(;_;_--)UesugiErii();
return 0;
}
::::