题解:P9464 [EGOI 2023] Padel Prize Pursuit / 追梦笼式网球
_Weslie_
·
·
题解
信心赛 T2。
Solution P9464
考虑优化暴力。我们发现,当一个人输了之后,他的奖牌将会给到胜者,一直到胜者输掉。而胜者输掉之后,他的所有奖牌又会给到打败胜者的人。假设胜者手中有 $x$ 块奖牌,那么这些奖牌到后面转移路径是一样的——这太浪费时间了!
于是你考虑从后往前扫一遍,到某个位置的时候记录一下最大的奖牌数和谁拥有最大的奖牌数,然后转移的时候从当前胜者失败的位置转移即可。但是你会发现样例 $3$ 就是错误的,因为这个无法处理一个人在不同两段之内拿到一块奖牌的情况。
于是考虑对每个时间(下文记作“位置”)开一个 map 维护,但是显然 MLE。
你要考虑我们空间复杂度的瓶颈在什么地方。如果 $x_i$ 的失败位置确定是 $i+1$(即 $y_{i+1}=x_i$),那么你就不需要对每个位置开一个 map 了,转移的时候直接修改 $i+1$ 位置的 map 即可。
但是现实很骨感,我们无法保证上面的性质,导致了我们转移可能需要任何一个位置的 map 的信息。
于是我们考虑换一种顺序遍历。
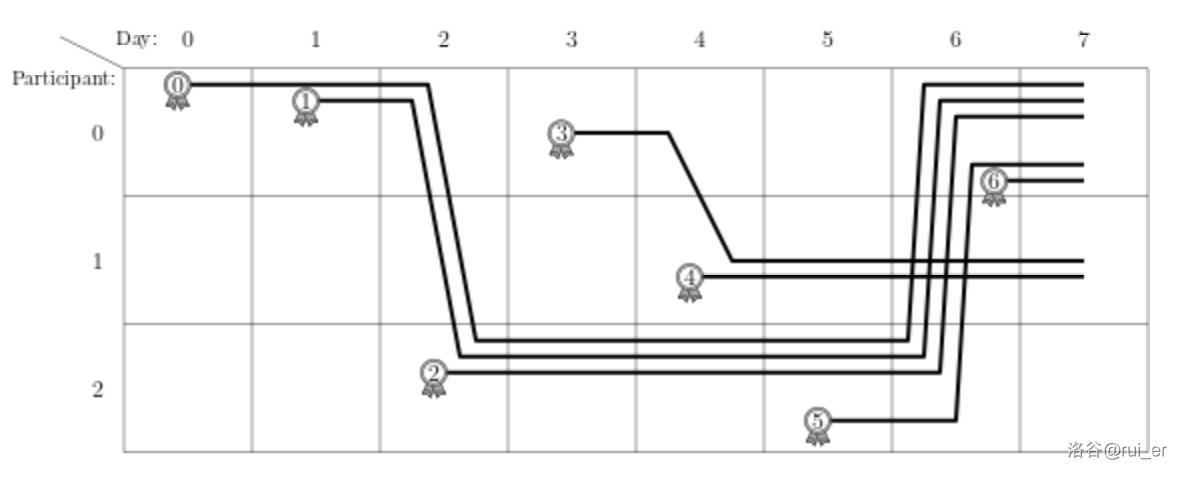
看这张图。如果我们在图的右边加一个超级汇点:
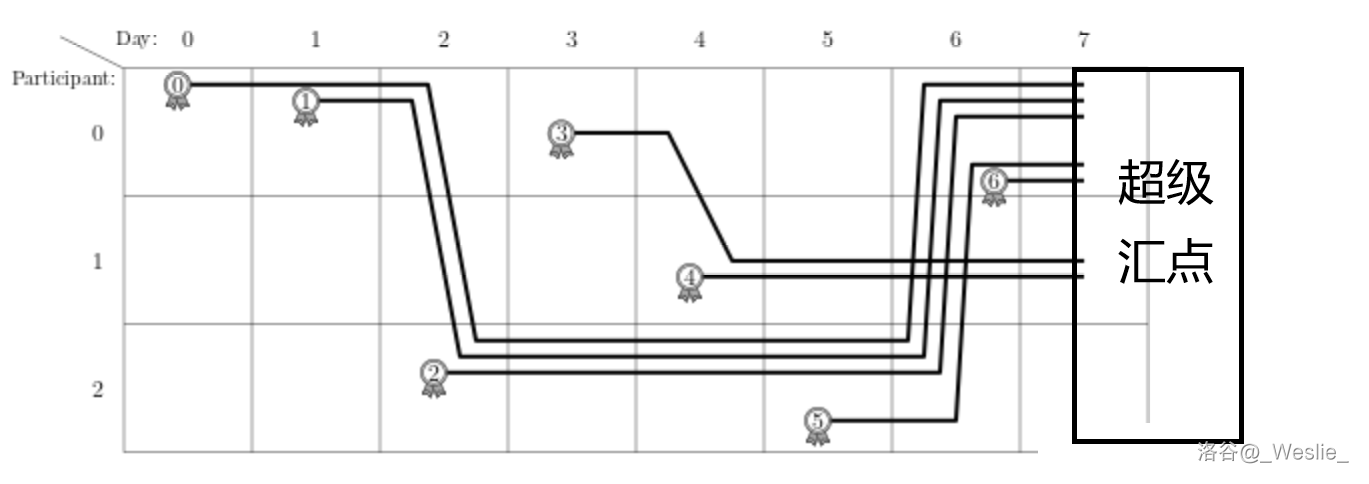
然后整个图形成了一个每条边都链接了时间 $i$ 和 $x_i$ 失败时间的树形结构。
看不懂?给你换一种方式看:
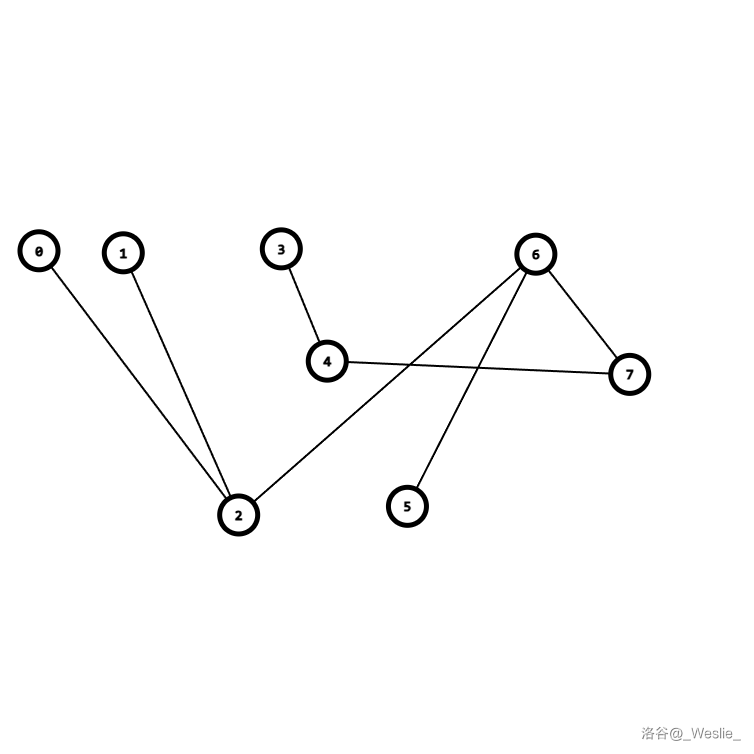
然后我们遍历这颗树,这棵树上有边权。边权是一个二元组 $(x,y)$,表示第 $x$ 个人时间增加 $y$。
由于子树内的点出来必然走过这条边,所以可以直接往上加,遍历完这棵子树之后再去掉这条边的影响即可。
那么你现在需要维护一个全局 $\max$ 位置和单点修改的东西,显然是线段树,然后你做完了。
::::success[Code]
```
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define fastio ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define ls (now<<1)
#define rs ((now<<1)|1)
using namespace std;
const int N=200005;
const int mod=1;
const int intinf=0x3f3f3f3f;
const ll llinf=0x3f3f3f3f3f3f3f3f;
int x[N],y[N],nxt[N];
int mx[N],pos[N],ans[N];
int n,m;
vector<int>g[N];
struct node{
int u,v,ps;int nxt;
ll w;
}e[N<<1];
int head[N],cnt;
void add(int u,int v,int ps,ll w){
e[++cnt].u=u;
e[cnt].v=v;
e[cnt].ps=ps;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
struct segtree{
int tr[N<<2],mxp[N<<2];
void pushup(int now){
if(tr[ls]>=tr[rs]){
tr[now]=tr[ls];
mxp[now]=mxp[ls];
}
else{
tr[now]=tr[rs];
mxp[now]=mxp[rs];
}
}
void build(int l,int r,int now){
if(l==r){
mxp[now]=l;
return;
}
int mid=(l+r)>>1;
build(l,mid,ls);
build(mid+1,r,rs);
pushup(now);
}
void update(int l,int r,int pos,int now,int x){
if(l==r){
tr[now]+=x;
return;
}
int mid=(l+r)>>1;
if(pos<=mid)update(l,mid,pos,ls,x);
if(pos>mid)update(mid+1,r,pos,rs,x);
pushup(now);
}
}tr;
void dfs(int now,int fa){
if(now!=m+1)ans[tr.mxp[1]]++;
for(int i=head[now],v;i;i=e[i].nxt){
v=e[i].v;
if(v==fa)continue;
tr.update(1,n,e[i].ps,1,e[i].w);
dfs(v,now);
tr.update(1,n,e[i].ps,1,-e[i].w);
}
}
signed main(){
// freopen("contest.in","r",stdin);
// freopen("contest.out","w",stdout);
fastio;
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>x[i]>>y[i];
x[i]++;y[i]++;
g[x[i]].push_back(i);
for(auto x:g[y[i]]){
nxt[x]=i;
}
g[y[i]].clear();
}
for(int i=1;i<=n;i++){
for(auto x:g[i]){
nxt[x]=m+1;
}
}
tr.build(1,n,1);
for(int i=1;i<=m;i++){
add(nxt[i],i,x[i],nxt[i]-i);
add(i,nxt[i],x[i],nxt[i]-i);
}
dfs(m+1,0);
for(int i=1;i<=n;i++){
cout<<ans[i]<<' ';
}
return 0;
}
```
::::