题解:P11452 [USACO24DEC] Cake Game S
orpg
·
·
题解
思路
不难发现,其实 Bessie 是没有选择的空间的,她只能合并最中间的两个蛋糕,不然的话 Elsie 就可以把 Bessie 合成的蛋糕藏起来。
举个例子。
如果有以下的蛋糕 :
Bessie 如果不合成中间两个蛋糕而选择合成 $[40,50]$。
第一步后:$[80,90,10,70,20]$。
对于 Elsie 最优选择是把 $80$ 藏起来。
第二步后:$[90,10,70,20]$。
所以不管 Bessie 之后怎么合 Elsie 都可以轻松的取走 Bessie 之前合成的东西。
---
所以,实际上整个游戏实际上是 Elsie 的主动权。整个题目就被简化成求 Elsie 的最大值。
在这之前我们先看一下两个人各能取多少个蛋糕。观察可得 Bessie 会在一开始拿走两个蛋糕,随后跟 Elsie 一样,一次取一个(因为 Bessie 只能合成最中间的两个)。所以不难发现 Bessie 一次可以取 $\frac{N}{2}+1$ 个,而 Elsie 一次可以取 $\frac{N}{2}-1$ 个(题目保证 $N$ 为偶数)。
对于 Elsie 不难发现,其实它是在不停的取左边或者右边。我们把该数列首尾拼接,则 Elsie 可以取到的蛋糕就是一个滑动的区间。
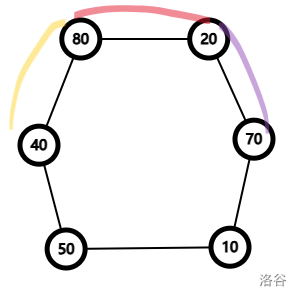
由上面的推理,不难得出 Elsie 只能拿 $\frac{N}{2}-1$ 个,在这里也就是 2 个,又因为 Elsie 只能从两边开始拿,所以它能拿的区间就是上图中的三个区间,最大值就显而易见了。
## 代码实现
我们可以把输入的数组重新存在原数组后面(以达到连接首尾的效果),然后对该数组求一个前缀和,这样可以快速的求出 Elsie 的最大值。然后把总其与总数相减,就是 Bessie 的答案了。
## code
```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e6+5;
int t,n;
int a[maxn];
ll sum[maxn];
ll all=0;
ll ans=0;
void init(){
memset(sum,0,sizeof sum);
ans=0;
all=0;
}
int main(){
cin>>t;
while(t--){
init();
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i],all+=a[i],a[i+n]=a[i];
int bessie=(n/2)+1,elsie=(n/2)-1;
for(int i=(n/2)+2;i<=(3*n/2)-1;i++) sum[i]=sum[i-1]+a[i];
for(int i=n;i<=(3*n/2)-1;i++){
ans=max(ans,sum[i]-sum[i-elsie]);
}
cout<<all-ans<<" "<<ans<<'\n';
}
}
```