CF932G 题解
zhylj
·
·
题解
题目描述
把字符串 s 划分成若干个字符串 t_1t_2\cdots t_k,使得 t_i=t_{k-i+1},求方案数,对 998244353 取模。
### 问题转化
记 $|s|=n$.
考虑将 $s$ 的后半部分翻转,然后逐个插入 $s$ 的前一半的相邻两个之间,那么字符串将变为:$s_1s_{n}s_2s_{n-1}\cdots$,我们发现,原划分方案恰好对应了对新串进行偶数长度的回文划分的方案,于是我们的问题变成了求偶数长度的回文划分方案数。
为了解决这个问题,我们先来考虑回文串和 border 的一系列性质。
(下面部分内容节选自我的[回文树入门博客](http://zhylj.cc/index.php/archives/26/))
### 周期
**周期**:对于字符串 $s$,若正整数 $p$ 满足 $\forall i\in[1,|s|-p]\cap \mathbf N, s_{i} = s_{i + p}$,则称 $p$ 为 $s$ 的周期。
记 $\operatorname{per}(u)$ 表示 $u$ 的最小周期。
**弱周期引理**:若 $p,q$ 为 $s$ 的周期,$p+q\le |s|$,则 $\gcd(p,q)$ 为 $s$ 的周期。
**证明**
不妨设 $q\ge p$,由 $p+q\le |s|$ 可推得对任意 $1\le i\le |s|$,有 $i-p>0$ 或 $i+q\le |s|$。
- 对于第一种情况,由周期定义可知 $s_i = s_{i-p} = s_{i-p+q}$。
- 对于第二种情况,由周期定义可知 $s_i = s_{i+q} = s_{i+q-p}$。
故 $d = q-p$ 为 $s$ 的周期,如此辗转相除可得 $\gcd(p,q)$ 为 $s$ 的周期。
(周期引理:$p,q$ 为 $s$ 的周期,$p+q-\gcd(p,q) \le |s|$,则 $\gcd(p,q)$ 为 $s$ 的周期)
### 匹配与 Border
**Border**:对于一个字符串 $s$,若 $t = \operatorname{pre}(s,x) = \operatorname{suf}(s,x)$,则 $t$ 为 $s$ 的一个 border.
**引理**:字符串 $s$ 存在一个长度为 $x$ 的 border 当且仅当 $|s| - x$ 为 $s$ 的周期。
**证明**:均等价于 $s_i = s_{|s| - |t| + i}$ 这个条件。
**引理**:若字符串 $u,v$ 满足 $|u|\le |v|\le 2|u|$,则 $u$ 在 $v$ 中的所有匹配位置构成一个等差数列。
只需要考虑匹配超过 $3$ 次的情况。
记第一次匹配与第二次匹配的间距为 $d$,第二次匹配与第 $x$ 次匹配的间距为 $q$.
由 $|u|\le |v|\le 2|u|$,显然 $u$ 在 $v$ 中的两次匹配的位置集合 $u_1,u_2$ 存在重叠部分,且长度为 $|u| - d
故 \operatorname{pre}(u,|u|-d) 为 u 的一个 border,即 d 为 u 的一个周期,同理 q 为 u 的一个周期。
而显然第一次匹配和第 x 次匹配的位置集合 u_1,u_x 同样存在重叠部分,故 d+q\le |u|,故 \gcd(d,q) 为 u 的周期。
若 d< \gcd(d,q),则我们可以将 u_2 向前移动构造在第一次第二次之间的匹配,矛盾。
故 d = \gcd(d,q),即 d\mid q。
由 u_i = u_{i+d},我们可以得到从第二次匹配开始到第 x 次匹配,每隔 d 个字符均会存在一个匹配,故命题得证。
由此证明我们可以得到一个推论:
推论:若字符串 u,v 满足 |u|\le |v|\le 2|u|,u 在 v 中的所有匹配位置构成了一个公差为 d,超过三项的等差数列,则 \operatorname{per}(u) = d.
接下来我们讨论 Border 的结构。
引理:字符串 s 的所有不小于 |s|/2 的 border 组成一个等差数列。
证明:对于最大的 border 和任意一个 border,设其长度分别为 n-p,n-q,可得 p,q 为 s 的周期,\gcd(p,q) 为 s 的周期,类似之前的方法可得 p\mid q。
(border 本质上就是在和自己匹配)
引理:若 |u|=|v|,记 \operatorname{LargePS}(u,v)=\{k\mid k\ge |u|/2,\operatorname{pre}(u,k)=\operatorname{suf}(v,k)\},则 \operatorname{LargePS}(u,v) 构成一个等差数列。
证明:设其中最大的元素为 x,则 x/2\le |u|/2,且其他元素均为 \operatorname{pre}(u,x) 的 border 的长度。接下来由前一个引理可证。
我们可以把一个字符串的所有 border 按照长度属于 [1,2),[2,4),\cdots,[2^k,n) 分类,第 i 类的元素为 \operatorname{LargePS}(\operatorname{pre}(s,2^i),\operatorname{suf}(s,2^i)).
于是我们得到了一个推论:
推论:字符串 s 的 border 可以被划分为 \mathcal O(\log n) 个等差数列。
回文后缀与 border
引理:s 是回文串,则 s 的后缀 t 是回文串当且仅当 t 是 s 的 border.
证明
两个条件均等价于 s_i = s_{|s|-i+1} = s_{|s|-(|t|-i + 1)+1} = s_{|s|-|t|+i}.
据此,易得:
推论:s 是回文串,则 s 的回文后缀可以被划分为 \mathcal O(\log n) 个等差数列。
slink 链与最小回文划分
slink 指针
记 \operatorname{diff}(x) = \operatorname{len}(x) - \operatorname{len}(\operatorname{fail}(x)),而 \operatorname{slink}(x) 表示回文树中 \operatorname{fail} 树上离 x 最近的满足 \operatorname{diff}(y)\neq \operatorname{diff}(x) 的 y。
显然这可以很容易在建回文树的时候维护出来。
容易发现,这意味着从 x 开始跳 \operatorname{fail} 指针,一直到跳到 y 之前,都是在一个等差数列上跳的。
也就是说,根据我们之前的推论,从某个点开始跳 slink 指针直到根节点,至多跳 \mathcal O(\log n) 步。
回文划分计数
例:给定一个字符串 s,求有多少划分 t_1t_2\cdots t_n = s,使得 t_1,t_2,\cdots,t_n 均为回文串。对 998244353 取模。
对于此题,我们考虑记 $f_i$ 表示长度为 $i$ 的前缀的回文划分方案数。
那么我们有一个显而易见的 dp 方程:
$$
f_i = \sum_{j} f_{i-j}[s[i-j+1,i] \text{ is palindromic}]
$$
直接暴力转移是 $\mathcal O(n^2)$ 的,我们考虑如何利用回文后缀的性质:
我们考虑在回文树上加入一个字符时,对应的节点所在的等差数列发生了什么样的变化:
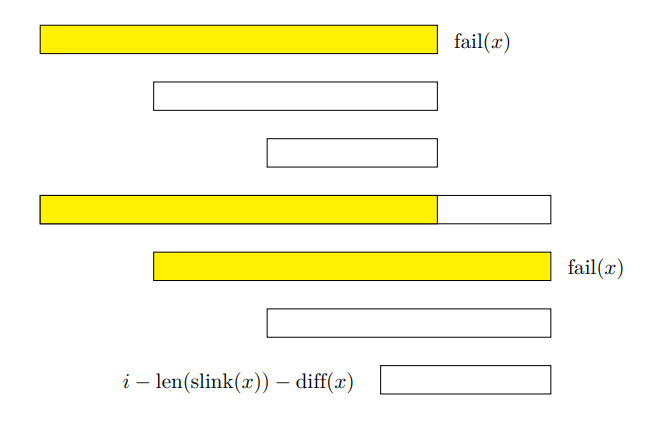
显然,等差数列中的所有回文串都是当前节点的后缀。
由于回文后缀同时是 border 的优美性质,等差数列中的所有回文后缀都在恰好平移了 $\operatorname{diff}(x)$(公差)个字符后再次出现,我们再观察 dp 值,发现这些回文串的 dp 值之和在加入这个节点前后仅仅差了一个位置:$f_{i-\operatorname{len}(\operatorname{slink}(x))-\operatorname{diff}(x)}$.
这启发我们,对回文树上的节点 $x$ 维护 $g_x$ 表示以 $x$ 开始到 $\operatorname{slink}(x)$ 以前,这条链上的回文子串**最后一次出现**所对应的 dp 值,那么我们可以很容易地从 $g_{\operatorname{fail}(x)}$ 转移到 $g_x$.
于是,对于一个新加入的节点,我们只需要暴力跳 $\operatorname{slink}$ 链并修改我们在 $\operatorname{slink}$ 链上跳过所有节点的 $g$ 即可(即用 $\operatorname{fail}(x)$ 更新 $x$)。
为什么这样做是对的呢?我们注意到 $\operatorname{fail}(x)$ 的上一次出现必然是在当前最长回文后缀的左端点处(否则与其是最长回文后缀的定义不符),故其 $g$ 的值一定如我们想象的那样记录了从当前最长回文后缀的左端点开始的一串等差数列对应的 dp 值。
根据我们先前证明的结论,该算法的时间复杂度为 $\mathcal O(n\log n)$.
#### 代码
```cpp
const kN = 1e6 + 5, kMod = 998244353;
int tr[kN][26], fch[kN][26], fail[kN], slink[kN], d[kN], s[kN], len[kN],
s_len, cur, node_cnt, f[kN], g[kN];
void Init() { node_cnt = 1; len[0] = -1; s[0] = -1; }
void Insert(int c) {
int p = s[s_len - len[cur]] == c ? cur : fch[cur][c];
s[++s_len] = c;
if(tr[p][c]) cur = tr[p][c];
else {
cur = tr[p][c] = ++node_cnt;
int fu = fail[cur] = p ? tr[fch[p][c]][c] : 1;
len[cur] = len[p] + 2; d[cur] = len[cur] - len[fu];
slink[cur] = d[fu] == d[cur] ? slink[fu] : fu;
for(int i = 0; i < 26; ++i)
fch[cur][i] = s[s_len - len[fu]] == i ? fu : fch[fu][i];
}
}
int n; char str[kN];
int main() {
scanf("%s", str + 1); n = strlen(str + 1);
Init(); f[0] = 1;
for(int i = 1; i <= n; ++i) {
Insert(str[i] - 'a');
for(int j = cur; j > 1; j = slink[j]) {
int dlt = len[slink[j]] + d[j];
g[j] = f[i - dlt];
if(fail[j] != slink[j]) {
g[j] = (g[j] + g[fail[j]]) % kMod;
}
f[i] = (f[i] + g[j]) % kMod;
}
}
printf("%d\n", f[n]);
}
```
### 回到本题
在本题中,我们需要求得一个字符串的偶数长度回文划分,于是考虑对 $g$ 的定义稍作修改:$g_{x,0/1}$ 表示只保留插入的回文串长度为奇数 / 偶数的 dp 值之和。
然后就可以写出代码了(详细代码和上面类似,这里只给出关键部分):
```cpp
for(int i = 1; i <= n; ++i) {
Insert(str[i] - 'a');
for(int j = cur; j > 1; j = slink[j]) {
int dlt = len[slink[j]] + d[j];
g[j][0] = g[j][1] = 0;
g[j][dlt & 1] = f[i - dlt];
if(fail[j] != slink[j]) {
for(int k = 0; k < 2; ++k)
g[j][k] = (g[j][k] + g[fail[j]][k ^ (d[j] & 1)]) % kMod;
}
f[i] = (f[i] + g[j][0]) % kMod;
}
}
```