题解 CF240E / 最小树形图及方案输出
warzone
·
·
题解
可能更好的阅读体验
题目大意
给定一 n 个点 m 条边的有向图,每条边边权为 0 或 1。
求该图以 1 为根的最小树形图,并输出最小树形图中所有边权为 1 的边。
无解输出 -1。保证没有重边。
注意为文件输入输出(输入到 `input.txt`,输出到 `output.txt`)。
# 题解
前置芝士:[最小树形图](https://www.luogu.com.cn/problem/P4716)
正解为 tarjan 优化朱刘算法 + 输出方案 。
本文将依次讲解 tarjan 优化朱刘算法、及最小树形图的方案输出。
约定以下记号:
- $u\rightarrow v$:从点 $u$ 到点 $v$ 的边。
- $\mathrm{val}_{u\rightarrow v}$:边 $u\rightarrow v$ 的权值。
- $\circlearrowright$:环。
- $\circlearrowright_u$:点 $u$ 所在的环。
- $\mathrm{lca}_{u,v}$:树上 $u,v$ 的最近公共祖先。
- $u\Rightarrow v$:点 $u$ 到点 $v$ 的路径(不包含 $v$)
## tarjan 优化朱刘算法求最小树形图
求解最小树形图的朱刘算法是一个典型的反悔贪心:
先选定每个非根结点的最小入边(去掉自环),若不形成环显然是最优解。
否则,显然形成的是 一棵树 + 若干基环树森林。
考虑反悔:对于某个环 $\circlearrowright$,
考虑断环为链,也就是将环上的某条边 $u\rightarrow v$ 替换为 $u'\rightarrow v\ (u'\notin\circlearrowright)$。
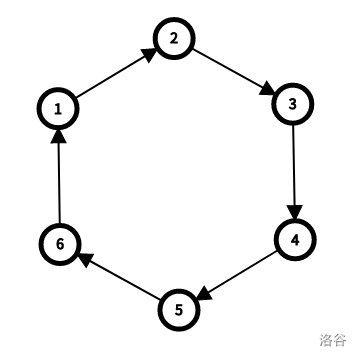
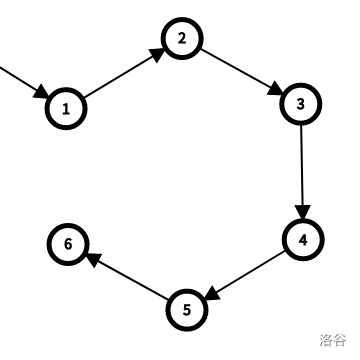
于是对于所有的 $u'\rightarrow v,\mathrm{val}_{u'\rightarrow v}\leftarrow\mathrm{val}_{u'\rightarrow v}-\mathrm{val}_{u\rightarrow v}$ ,之后缩点并重复最开始的步骤即可。
-----------------------------
这个过程是可以用可并堆优化的:
对于每个点,用一个堆存储其所有入边。
- 选定最小入边即取出堆中最小元素。
- $\mathrm{val}_{u'\rightarrow v}\leftarrow\mathrm{val}_{u'\rightarrow v}-\mathrm{val}_{u\rightarrow v}$ 即堆的整体加减(打标记实现)。
- 缩点时合并入边即合并多个堆。
tarjan 老爷子指出,反悔可在贪心选择方案时实时进行。
具体地,依次选择每个非根结点的最小入边(去掉自环)时,
一旦出现了环,就可以立即反悔缩点。
缩点仅涉及之前选过入边的点,因此接下来尝试对新缩得的点和剩下的点选择最小入边即可。
判环和缩点可分别用一个并查集判定。
```cpp
typedef long long ll;
typedef unsigned int word;
typedef unsigned char byte;
#define floor floor_
word from[100010],to[100010];
byte value[100010];
struct heap{//可并堆
heap *l,*r;
word floor;
int value,tag;
inline void operator+=(int num){
value+=num,tag+=num;}
inline void pushdown(){
if(l) *l+=tag;
if(r) *r+=tag;
tag=0;
}
inline void pushup(){
if(l==0) l=r,r=0;
else if(r&&l->floor<r->floor){
register heap* swap=l;
l=r,r=swap;
}
floor=r? r->floor+1:1;
}
}p[100010],*rt[200010];
inline heap* merge(heap *l,heap *r){//合并堆
if(l==0) return r;
if(r==0) return l;
if(l->value>r->value){
register heap* swap=l;
l=r,r=swap;
}
l->pushdown(),l->r=merge(l->r,r);
return l->pushup(),l;
}
word n,m,psiz,root,fa[200010];
struct union_{//并查集
word fa[200010];
inline union_(){
for(register word i=1;i<=200000;++i) fa[i]=i;}
inline word find(word id){
if(fa[id]==id) return id;
return fa[id]=find(fa[id]);
}
inline bool merge(word rt,word ch){
rt=find(rt),ch=find(ch);
if(rt!=ch) return fa[ch]=rt,1;
return 0;
}
}ring,tree;
word stack[100010],stacksiz,belong[200010];
inline ll DMST(){
ll ans=0;psiz=n;
for(word i=1,u,id;i<=n;++i)
if(belong[id=i]=root,i!=root) for(heap *get;;){ //选定最小入边
if((get=rt[id])==0) return -1; //选边失败
get->pushdown(),rt[id]=merge(get->l,get->r); //取出最小入边
if((u=ring.find(from[get-p]))==id) continue; //忽略自环
if(ans+=get->value,rt[id]) *(rt[id])+=-get->value; //反悔
stack[++stacksiz]=get-p; //记录选边
if(u==root){ring.merge(root,id);break;} //与根连通,不可能成环
if(tree.merge(u,id)){fa[id]=u;break;} //并查集判环
tree.merge(++psiz,id),rt[psiz]=rt[id]; //缩点(新开一个点)
while(u!=id){
belong[u]=psiz,ring.merge(psiz,u);
rt[psiz]=merge(rt[psiz],rt[u]); //合并入边
u=(fa[u]=ring.find(fa[u]));
}
ring.merge(psiz,id);
belong[id]=psiz,belong[id=psiz]=root;
}
return ans;
}
```
注意缩点的时候新开一个点,这样便于之后记录方案。
## 最小树形图的方案记录
朱刘算法只能给出加入的边及其加入次序,并不能直接指出哪些边被替换了。
原因是 “环套环” 的情况下一条边可能替换多条边。
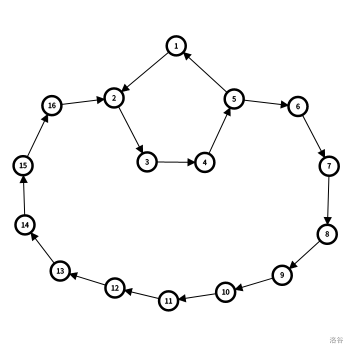
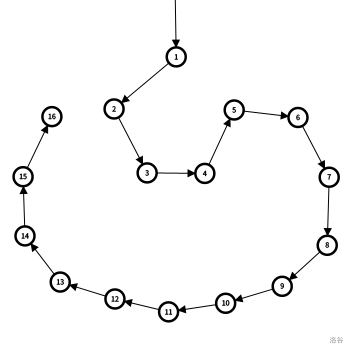
但朱刘算法运行过程中,每个点与其所属强连通分量形成了树结构,称为收缩树。
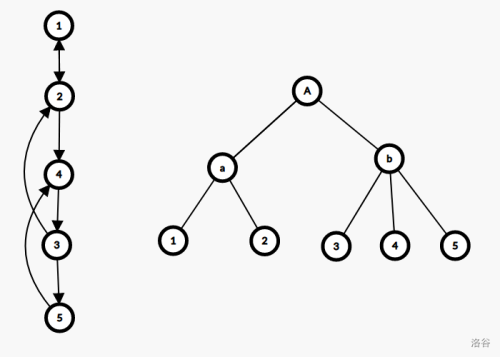
收缩树反映了缩点前后原图的状态。
因此,原图上每条边 $u\rightarrow v$ 会作为收缩树上 $v\Rightarrow \mathrm{lca}_{u,v}$ 上点的入边。
因此可按加入次序反向检查冲突:
对于边 $u\rightarrow v$,若收缩树上 $v\Rightarrow \mathrm{lca}_{u,v}$ 上某个点已经有入边了,那就不加入这条边。
```cpp
typedef unsigned int word;
typedef unsigned char byte;
word head[200010],next[200010];
word size[200010],floor[200010];
word son[200010],newid[200010],step;
template<word size>
struct segment_tree{//线段树
segment_tree<(size>>1)> l,r;
byte tag,sum;
inline byte operator()(word f,word t){
if(tag) return 1;
if(f==0&&t==(size<<1)-1) return sum;
if(f&size) return r(f&~size,t&~size);
else if((t&size)^size) return l(f,t);
return l(f,size-1)||r(0,t&~size);
}
inline void operator()(word f,word t,byte num){
if(tag) return;
if(f==0&&t==(size<<1)-1)
return sum|=num,void(tag|=num);
if(f&size) r(f&~size,t&~size,num);
else if((t&size)^size) l(f,t,num);
else l(f,size-1,num),r(0,t&~size,num);
sum=l.sum|r.sum;
}
};
template<>
struct segment_tree<0>{
byte sum;
inline void operator()(word f,word t,byte num){sum|=num;}
inline byte operator()(word f,word t){return sum;}
};
segment_tree<(1u<<17)> segtree;
inline void dfs1(word id){
size[id]=1;
for(register word i=head[id];i;i=next[i]){
floor[i]=floor[id]+1;
dfs1(i),size[id]+=size[i];
if(size[son[id]]<size[i]) son[id]=i;
}
}
inline void dfs2(word id){
newid[id]=++step;
if(son[id]) size[son[id]]=size[id],dfs2(son[id]);
for(register word i=head[id];i;i=next[i])
if(i!=son[id]) size[i]=i,dfs2(i);
}
inline void getMST(){
for(register word i=1;i<=psiz;++i)
if(i!=root) next[i]=head[belong[i]],head[belong[i]]=i;
dfs1(root),size[root]=root,dfs2(root);//树剖预处理
for(word u,v,id,get;stacksiz;--stacksiz){
get=0,id=stack[stacksiz];
for(u=from[id],v=to[id];size[u]!=size[v];)
if(floor[size[u]]>floor[size[v]]) u=belong[size[u]];
else{
get|=segtree(newid[size[v]],newid[v]);
v=belong[size[v]];
}
if(floor[u]<floor[v]) get|=segtree(newid[u]+1,newid[v]);
//检查 v => lca(u,v) 上是否有入边
if(get) continue;
if(value[id]) printf("%u\n",id);
for(u=from[id],v=to[id];size[u]!=size[v];)
if(floor[size[u]]>floor[size[v]]) u=belong[size[u]];
else{
segtree(newid[size[v]],newid[v],1);
v=belong[size[v]];
}
if(floor[u]<floor[v]) segtree(newid[u]+1,newid[v],1);
//将 u->v 作为 v => lca(u,v) 上点的入边
}
}
```
就此,我们以比原算法多出一倍的码量,完成了最小树形图的方案记录。