TJ For GSS6
Tiffake
·
·
题解
题目描述
给你一个长度为 n 的序列。
有 m 次操作,单点插入,单点删除,单点修改,求区间最大子段和。
### 思路
~~不说啥了,虽然平衡树可以,但是我不会,所以写了个平衡线段树。~~
如果想学平衡树,应该径直走向其他题解。
考虑线段树如何插入。
答案是线段树不能插入,吗?
考虑最简单的情况,整棵线段树只有一个数,我们该如何插入?显然,只需要让那个数变成它的兄弟节点,然后再搞个父亲把它俩连起来就行了。
考虑将上述情况拓展,如果你有很多数该怎么办。我们可以先在线段树中找到插入位置的那个数,接着对它和插入的数经行上述操作即可,代码如下。
```cpp
inline void insnode(int k,int x,int v){
int ls=++tot,rs=++tot;//新开两个节点存储(这是动态开点的线段树)
if(x!=s[k].l)s[rs].sz=1,s[rs].l=s[rs].r=s[k].l+1,chnode(rs,v),s[ls]=s[k];
//上面的条件是特判插入的数不存在(在n之后),这时候需要把插入的数放在右儿子
else s[ls].sz=1,s[ls].l=s[ls].r=x,chnode(ls,v),s[rs]=s[k],s[rs].l=s[rs].r=x+1;
merge(k,ls,rs);//记得把左右儿子合并到这个节点
}
```
但是该怎么更新线段树的区间下标呢?我们不一定得一次改完,可以写两个类似 `pushup`、`pushdown` 的函数一步步改。
所以分为两种情况更新:
1. 自底向上时,我们可以保证左儿子的区间下标是对的(毕竟是在某个数前插入),因此直接把右区间贴到左区间右边,同时更新父亲的右节点即可。代码:
```cpp
inline void crtup(int k,int ls,int rs){
if(!s[ls].sz&&!s[rs].sz)return;//如果没有儿子就没必要更新。
s[rs].l=s[ls].r+1,s[k].r=s[rs].r=s[ls].r+s[rs].sz;
}
```
2. 自顶向下时,我们可以保证父亲的区间下标是对的(毕竟已经更新过了),因此直接把左区间贴到父亲区间左边,右区间贴到父亲区间的右边即可。代码:
```cpp
inline void crtdown(int k,int ls,int rs){
if(!s[ls].sz&&!s[rs].sz)return;//如果没有儿子也没必要更新。
s[ls].l=s[k].l,s[ls].r=s[k].l+s[ls].sz-1;
s[rs].l=s[ls].r+1,s[rs].r=s[k].r;
}
```
删除也和插入类似,只需要把这个节点的所有东西还原成最初始的样子就行,代码就不给了。
但要是真这样写,稍微想想就知道,只要一直往一个地方插入,这颗线段树就会退化成一条链,然后时间复杂度就变成 $O(n)$ 了。所以我们需要一种平衡操作来防止这种情况的发生。
考虑一下不平衡的定义,当某棵子树的一个儿子远远大于它的另一个儿子时,这棵树就变得不平衡了。当这个“远远大于”取 $3$ 倍时可以使树高不超过 $2\log_2n$ 并且最好写。
分五种情况讨论该如何平衡:
1. 左儿子比右儿子大,左儿子的左儿子比左儿子的右儿子大,如图。
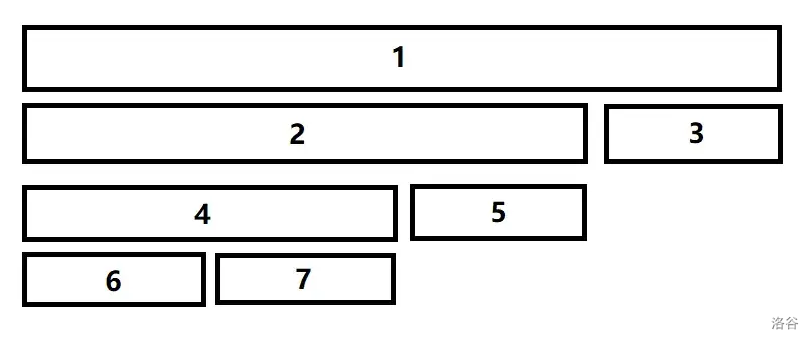
直接让 `s[2]=merge(s[5],s[3])`,然后 `s[1].ls=4,s[1].rs=2` 即可。
2. 左儿子比右儿子大,左儿子的左儿子比左儿子的右儿子小,如图。
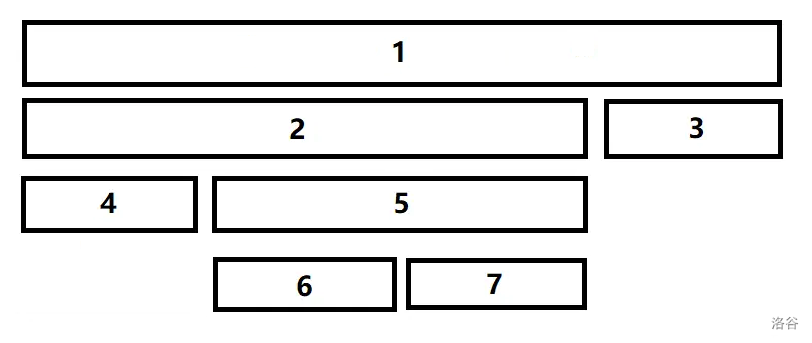
先 `s[2]=merge(s[4],s[6])`,再 `s[5]=merge(s[7],s[3])`,最后 `s[1].ls=2,s[1].rs=5` 即可。
3. 左儿子比右儿子小,右儿子的左儿子比右儿子的右儿子小,如图。
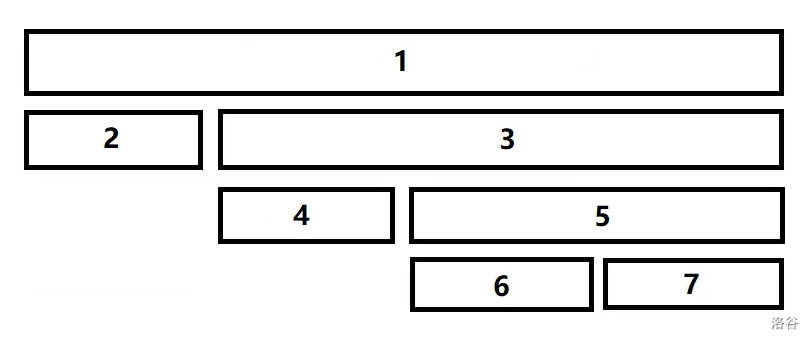
和情况一类似,只需要 `s[3]=merge(s[2],s[4]),s[1].ls=3,s[1].rs=5` 即可。
4. 左儿子比右儿子小,右儿子的左儿子比右儿子的右儿子大,如图。
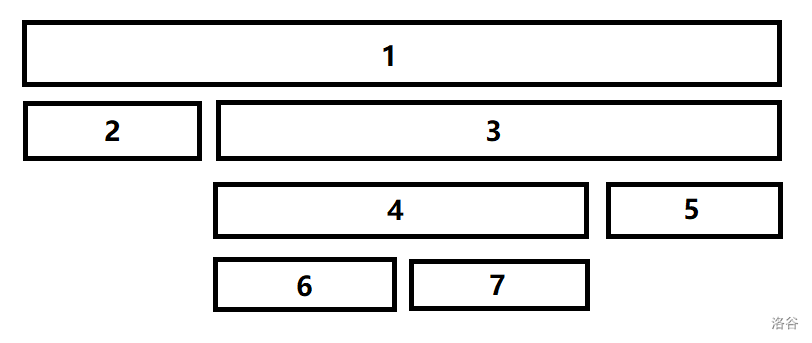
和情况二类似,只需要 `s[4]=merge(s[2],s[6]),s[3]=merge(s[7],s[5]),s[1].ls=4` 即可。
5. 没有左儿子或右儿子。直接把根节点改为剩下的节点即可。
需要注意的是,一定不能把合并的顺序写错了,代码如下:。
```cpp
inline void equil(int k){
int ls=s[k].ls,rs=s[k].rs,x;
if(!s[ls].sz)return s[k]=s[rs],s[rs].clear();
if(!s[rs].sz)return s[k]=s[ls],s[ls].clear();
if(min(s[ls].sz,s[rs].sz)*3>max(s[ls].sz,s[rs].sz))return;
if(s[ls].sz>s[rs].sz)
if(s[s[ls].ls].sz>=s[s[ls].rs].sz)s[k].ls=s[ls].ls,merge(ls,s[ls].rs,rs),s[k].rs=ls;
else x=s[ls].rs,merge(ls,s[ls].ls,s[x].ls),merge(x,s[x].rs,rs),s[k].rs=x;
else
if(s[s[rs].ls].sz<=s[s[rs].rs].sz)s[k].rs=s[rs].rs,merge(rs,ls,s[rs].ls),s[k].ls=rs;
else x=s[rs].ls,merge(rs,s[x].rs,s[rs].rs),merge(x,ls,s[x].ls),s[k].ls=x;
}
```
然后就完了,值得一提的是,它的常数略小于 `FHQ-Treap`。
给出完整代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+1;
struct node{
int ls,rs,l,r,sz;
long long t,mx,pre,suf;
node(){ls=rs=l=r=t=sz=0,pre=suf=mx=INT_MIN;}
inline void clear(){l=r=t=sz=0,pre=suf=mx=INT_MIN;}
}s[N<<2];
int tot,n,m,a[N];
inline void crtup(int k,int ls,int rs){
if(!s[ls].sz&&!s[rs].sz)return;
s[rs].l=s[ls].r+1,s[k].r=s[rs].r=s[ls].r+s[rs].sz;
}
inline void crtdown(int k,int ls,int rs){
if(!s[ls].sz&&!s[rs].sz)return;
s[ls].l=s[k].l,s[ls].r=s[k].l+s[ls].sz-1;
s[rs].l=s[ls].r+1,s[rs].r=s[k].r;
}
inline node merge(int k,int x,int y){
crtup(k,x,y);
s[k].l=s[x].l,s[k].r=s[y].r,s[k].sz=s[k].r-s[k].l+1,s[k].ls=x,s[k].rs=y;
s[k].mx=max(max(s[x].mx,s[y].mx),s[x].suf+s[y].pre);
s[k].pre=max(s[x].t+s[y].pre,s[x].pre);
s[k].suf=max(s[y].t+s[x].suf,s[y].suf);
s[k].t=s[x].t+s[y].t;
return s[k];
}
inline node merge(node x,node y){
node k;
k.mx=max(max(x.mx,y.mx),x.suf+y.pre);
k.pre=max(x.t+y.pre,x.pre);
k.suf=max(y.t+x.suf,y.suf);
k.t=x.t+y.t;
return k;
}
inline void equil(int k){
int ls=s[k].ls,rs=s[k].rs,x;
if(!s[ls].sz)return s[k]=s[rs],s[rs].clear();
if(!s[rs].sz)return s[k]=s[ls],s[ls].clear();
if(min(s[ls].sz,s[rs].sz)*3>max(s[ls].sz,s[rs].sz))return;
if(s[ls].sz>s[rs].sz)
if(s[s[ls].ls].sz>=s[s[ls].rs].sz)s[k].ls=s[ls].ls,merge(ls,s[ls].rs,rs),s[k].rs=ls;
else x=s[ls].rs,merge(ls,s[ls].ls,s[x].ls),merge(x,s[x].rs,rs),s[k].rs=x;
else
if(s[s[rs].ls].sz<=s[s[rs].rs].sz)s[k].rs=s[rs].rs,merge(rs,ls,s[rs].ls),s[k].ls=rs;
else x=s[rs].ls,merge(rs,s[x].rs,s[rs].rs),merge(x,ls,s[x].ls),s[k].ls=x;
}
inline void chnode(int k,int v){
s[k].mx=s[k].pre=s[k].suf=s[k].t=v;
}
inline void insnode(int k,int x,int v){
int ls=++tot,rs=++tot;
if(x!=s[k].l)s[rs].sz=1,s[rs].l=s[rs].r=s[k].l+1,chnode(rs,v),s[ls]=s[k];
else s[ls].sz=1,s[ls].l=s[ls].r=x,chnode(ls,v),s[rs]=s[k],s[rs].l=s[rs].r=x+1;
merge(k,ls,rs);
}
#define mid s[ls].r
#define ls s[k].ls
#define rs s[k].rs
void build(int k,int l,int r){
s[k].l=l,s[k].r=r;
if(l==r)return chnode(k,a[l]),s[k].sz=1,void();
ls=k<<1,rs=k<<1|1,build(ls,l,(l+r)>>1),build(rs,((l+r)>>1)+1,r);
merge(k,ls,rs);
}
void ins(int k,int x,int v){
crtdown(k,ls,rs);
if(s[k].l==s[k].r)return insnode(k,x,v),void();
if(x<=mid)ins(ls,x,v);
else ins(rs,x,v);
merge(k,ls,rs),equil(k);
}
void del(int k,int x){
crtdown(k,ls,rs);
if(s[k].l==s[k].r)return s[k].clear();
if(x<=mid)del(ls,x);
else del(rs,x);
merge(k,ls,rs),equil(k);
}
void change(int k,int x,int v){
crtdown(k,ls,rs);
if(s[k].l==s[k].r)return chnode(k,v);
if(x<=mid)change(ls,x,v);
else change(rs,x,v);
merge(k,ls,rs);
}
node mxsum(int k,int x,int y){
crtdown(k,ls,rs);
if(x<=s[k].l&&s[k].r<=y)return s[k];
node lres,rres;
if(x<=mid)lres=mxsum(ls,x,y);
if(y>mid)rres=mxsum(rs,x,y);
return merge(lres,rres);
}
char op;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
build(1,1,n),tot=n<<2,cin>>m;
for(int i=1,x,y;i<=m;i++){
cin>>op>>x;
switch(op){
case 'I':cin>>y,ins(1,x,y);break;
case 'D':del(1,x);break;
case 'R':cin>>y,change(1,x,y);break;
case 'Q':cin>>y,cout<<mxsum(1,x,y).mx<<'\n';break;
}
}
return 0;
}
```
~~后话:这种本质仍然是平衡树的线段树虽然也可以区间修改,但好像并没有什么用。~~