6th-2006西部
VinstaG173
·
·
个人记录
Day 1
题 1. 设 n 是给定的正整数,n \ge 2, a_1,a_2,\dots,a_n \in (0,1). 求 \sum\limits_{i=1}^{n}\sqrt[6]{a_i(1-a_{i+1})} 的最大值,这里 a_{n+1}=a_1.
思路 要把 6 次根号去掉,一个很自然的想法是用 AM-GM 不等式,有 \sqrt[6]{a_i(1-a_{i+1})\cdot\left(\dfrac{1}{2}\right)^4} \le \dfrac{1}{2}+\dfrac{a_i-a_{i+1}}{6}. 求和得 \sum\limits_{i=1}^{n}\sqrt[6]{a_i(1-a_{i+1})} \le \dfrac{\sqrt[3]{4}}{2}n, 当 a_i=\dfrac{1}{2} 时取等。
题 2. 求满足下述条件的最小正实数 k: 对任意不小于 k 的 4 个互不相同的实数 a,b,c,d, 都存在 a,b,c,d 的一个排列 p,q,r,s, 使得方程 (x^2+px+q)(x^2+rx+s)=0 有 4 个互不相同的实数根。
思路 当 k<4 时,在 \left[k,2\sqrt{k}\right] 中选择 a,b,c,d, 则 p^2-4q \le 0, 显然不满足条件。k \ge 4 时简单讨论即可。
题 3. 在 \triangle{PBC} 中,\angle{PBC}=60\degree, 过点 P 作 \triangle{PBC} 的外接圆 \omega 的切线,与 CB 的延长线交于点 A. 点 D,E 分别在线段 PA 和圆 \omega 上,使得 \angle{DBE}=90\degree, PD=PE. 连接 BE, 与 PC 交于点 F. 已知 AF,BP,CD 三线共点。
$(2)$ 求 $\tan{\angle{PCB}}$ 的值。
**思路** 先上图。
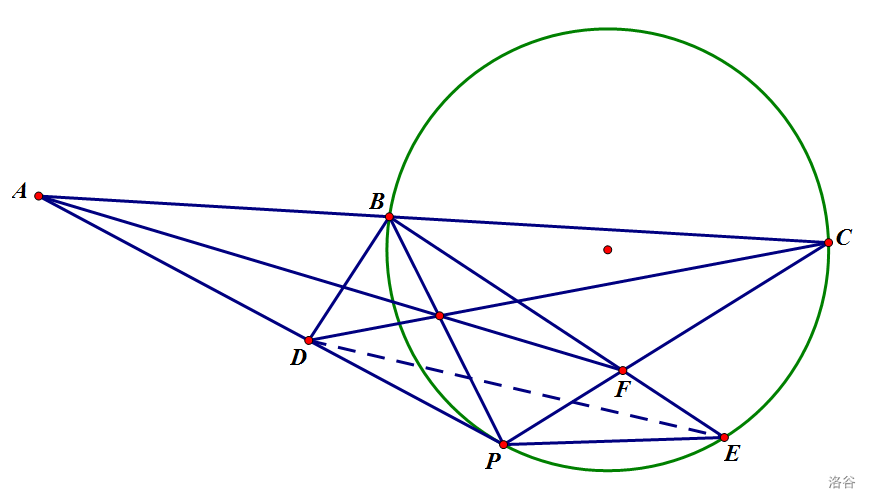
看到三线共点首先想 Ceva.事实上用正弦将 $AD,DP,PF,FC$ 转化到 $AB,BP,BC$ 上推导三角函数即可解决 $(1).
对于 (2), 注意到
\angle{DEP}&=\dfrac{1}{2}\left(180\degree-\angle{DPE}\right)\\
&=\dfrac{1}{2}\angle{EBP}=15\degree,
\end{aligned}
设 \angle{PCB}=\theta, 则
\cos\left(\theta-15\degree\right)&=\dfrac{BE}{DE}\\
&=\dfrac{2R\sin\left(\theta+30\degree\right)}{PE \cdot 2\cos{15\degree}}\\
&=\dfrac{\sin\left(\theta+30\degree\right)}{2\sin{30\degree}\cos{15\degree}},
\end{aligned}
即可解得 \tan{\theta}=\dfrac{6+\sqrt{3}}{11}.
题 4. 设正整数 a 不是完全平方数,求证:对每一个正整数 n, S_n=\{\sqrt{a}\}+\{\sqrt{a}\}^2+\dots+\{\sqrt{a}\}^n 的值都是无理数。
思路 设 \{\sqrt{a}\}=t,[\sqrt{a}]=r. 设 t^{n+1}=m+l\sqrt{a}, m,l \in \mathbb{Z}. 显然
(1-t)S_n&=t-t^{n+1}\\
&=(1-l)\sqrt{a}-(m+r).
\end{aligned}
若 S_n 为有理数,则 (1+r)S_n+r+m=(S_n+1-l)\sqrt{a}, 因此 S_n=l-1. 由 0<S_n<n 得 1<l<n+1, 容易推出矛盾。
Day 2
题 5. 设 S=\{n \mid n-1,n,n+1 都可以表示成两个正整数的平方和\}. 证明:若 n \in S, 则 n^2 \in S.
思路 由于 a,b 均可以表示成两正整数平方和时 ab 亦可表示,而 n^2+1 显然已满足,n^2=n \cdot n, n^2-1=(n-1)(n+1), 故 n^2 \in S.
题 6. AB 是圆 O 的直径,C 为 AB 延长线上的一点,过点 C 作圆 O 的割线,与圆 O 交于 D,E 两点,OF 是 \triangle{BOD} 的外接圆 O_1 的直径,连接 CF 并延长交圆 O_1 于点 G. 求证:O,A,E,G 四点共圆。
思路 先上图。
想证共圆要找角相等。发现 \angle{AEO} 和 \angle{AGO} 相比其他角对略微好看一点,因为画图能够注意到 A,C,D,G 共圆,可以方便地处理 \angle{AGO}.
具体地,由于
\angle{CGD}&=\angle{DOF}\\
&=\dfrac{1}{2}\angle{BOD}\\
&=\angle{DAB},
\end{aligned}
故 A,C,D,G 共圆。故
\angle{AGO}&=\angle{AGD}-\angle{DGO}\\
&=(180\degree-\angle{ACD})-\angle{DBC}\\
&=\angle{CDB}=\angle{CAE}=\angle{AEO},
\end{aligned}
故 O,A,E,G 共圆。
题 7. 设 k 是一个不小于 3 的正整数,\theta 是一个实数。证明:如果 \cos{(k-1)\theta} 和 \cos{k\theta} 都是有理数,那么存在正整数 n>k, 使得 \cos{(n-1)\theta} 和 \cos{n\theta} 都是有理数。
思路 根据 Chebyshev 多项式,有 \cos{n\alpha} 可以表示成 \cos{\alpha} 的整系数多项式,故 \cos{\alpha}\in\mathbb{Q} 时亦有 \cos{n\alpha}\in\mathbb{Q}. 在原题中取 n=k^2 即可。
题 8. 给定正整数 n(\ge 2), 求 \lvert X \rvert 的最小值,使得对集合 X 的任意 n 个二元子集 B_1,B_2,\dots,B_n, 都存在集合 X 的一个子集 Y, 满足:
(1)$ $\lvert Y \rvert=n;
(2)$ 对 $i=1,2,\dots,n,$ 都有 $\lvert Y \cap B_i \rvert \le 1.
思路 显然当 \lvert X \rvert \le 2n-2 时,将其中元素先成对分组,若最终剩余一个元素则任取另一个元素分组,则组数不超过 n-1, 任意 Y 至少包含其中一组。故 \lvert X \rvert \ge 2n-1.
当 \lvert X \rvert=2n-1 时,考虑 X 中元素在 B_i 中出现次数较少的,显然 Y 中元素出现次数越少越好。
如果有 \ge n-1 个元素没出现过,则 Y 由它们中的 n-1 个与任一个其他元素组成即可。
否则设有 x(<n-1) 个元素没出现过。则有 y 个元素只出现过一次。则剩下 2n-1-x-y 个元素至少出现 2 次。对 B_i 中元素总数算两次,有 y+2(2n-1-x-y) \le 2n, 故 x+1+\dfrac{1}{2}y \ge n. 我们将 x 个没出现过的元素放入 Y, 考虑在剩下元素中找 \left\lfloor\dfrac{1}{2}y\right\rfloor+1 个。若 y 个出现 1 次的元素中有任意一个与一个出现至少 2 次的元素在一个 B_i 中,则至少有 \left\lfloor\dfrac{1}{2}y\right\rfloor+1 个 B_i 包含一个出现 1 次的元素,从中各取一个即可。否则我们显然可以取出 \left\lfloor\dfrac{1}{2}y\right\rfloor 个出现 1 次的元素,在其他 B_i 中任取一个即可。